Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng

Thanh Dung Ngày: 05-01-2023 Lớp 10

629

Với giải Bài 75 trang 98 SBT Toán lớp 10 Cánh diều chi tiết trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 7

Bài 75 trang 98 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng 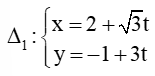và $Δ_{2}$ :

Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰;

B. 45⁰;

C. 90⁰;

D. 60⁰.

Lời giải:

Ta thấy vectơ chỉ phương của $Δ_{1}$ là: $\vec{u_{1}}$ =( $\sqrt{3}$ ;3)

Vectơ chỉ phương của $Δ_{2}$ là: $\vec{u_{2}}$ =(- $\sqrt{3}$ ;-1)

Ta có: cos( $\vec{u_{1}}$ , $\vec{u_{2}}$ )

= Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆1 x=2+(căn3)t, y=-1+3t và ∆2 x=3-(căn3)t', y=-t'

Suy ra ( $\vec{u_{1}}$ , $\vec{u_{2}}$ ) = 150^o

Suy ra góc giữa 2 đường thẳng chính là góc nhọn giữa 2 vectơ chỉ phương của 2 đường thẳng đó.

Do đó ( $Δ_{1}$ , $Δ_{2}$ )=180^o-( $\vec{u_{1}}$ , $\vec{u_{2}}$ )=30^o

Vậy chọn đáp án A.

Xem thêm lời giải SBT Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 71 trang 97 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(- 2; 1), B(1; - 3). Tọa độ của vectơ $\vec{A B}$ là:...

Bài 72 trang 97 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-1; - 5), B(5; 2) và trọng tâm là gốc tọa độ. Tọa độ điểm C là:...

Bài 73 trang 98 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, vectơ nào sau đây có độ dài bằng 1?...

Bài 74 trang 98 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, đường thẳng ∆ đi qua điểm M(- 2; 0) và song song với đường thẳng d: 2x – y + 2 = 0 có phương trình là:...

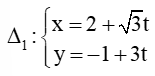
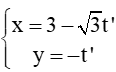
Bài 75 trang 98 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng và : ...

Bài 76 trang 98 SBT Toán 10 Tập 2: Khoảng cách từ điểm M(4; - 2) đến đường thẳng ∆: x – 2y + 2 = 0...

Bài 77 trang 98 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình đường tròn?...

Bài 78 trang 98 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình chính tắc của đường hypebol?...

Bài 79 trang 98 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình chính tắc của đường parabol?...

Bài 80 trang 99 SBT Toán 10 Tập 2: Đường elip $\frac{x^{2}}{40} + \frac{y^{2}}{36}$ =1 có hai tiêu điểm là:...

Bài 81 trang 99 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 3; - 1), B(3; 5), C(3; - 4). Gọi G, H, I lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC...

Bài 82 trang 99 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm F₁(- 4; 0) và F₂ (4; 0)...

Bài 83 trang 99 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 1; - 2), đường trung tuyến kẻ từ B và đường cao kẻ từ C lần lượt có phương trình là 5x + y – 9 = 0 và x + 3y – 5 = 0. Tìm tọa độ của hai điểm B và C...

Bài 84 trang 99 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 0) và B(0; 3). Tìm tập hợp các điểm M thỏa mãn MA = 2MB...

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

SBT Toán 10 Bài 3: Phương trình đường thẳng

SBT Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

SBT Toán 10 Bài 5: Phương trình đường tròn

SBT Toán 10 Bài 6: Ba đường conic

SBT Toán 10 Bài tập cuối chương 7

Từ khóa :

toán 10 Bài tập cuối chương VII

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

145

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

120

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

107

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

100

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.