Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
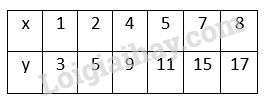
Bài 1 trang 60 SBT Toán 9 tập 1: Trong các bảng sau ghi các giá trị tương ứng của và .
Bảng nào xác định là hàm số của ? Vì sao?
a)
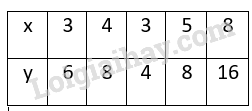
b)
Phương pháp giải:
Sử dụng:
Khái niệm về hàm số: Nếu đại lượng phụ thuộc vào đại lượng thay đổi sao cho với mỗi giá trị của ta luôn xác định được chỉ một giá trị tương ứng của thì được gọi là hàm số của .
Kí hiệu .
Lời giải:
a)
Xác định là hàm số của biến số vì với mỗi giá trị của ta xác định được một giá trị tương ứng duy nhất của
b)
Xác định không phải là hàm số của biến số vì với mỗi giá trị của ta xác định được hai giá trị khác nhau của
Ví dụ thì và .
; ; ; ; ; ; ;
; ; ; ; ; ; ;
; ; ; ; ; ;
Phương pháp giải:
Tính bằng cách thay vào .
Lời giải:
Tính bằng cách thay vào ta được các bảng sau:



; ; ; ; ;
; ; ; ; .
Phương pháp giải:
Tính bằng cách thay vào .
Lời giải:
Bài 4 trang 60 SBT Toán 9 tập 1: Cho hàm số với
Chứng minh rằng hàm số đồng biến trên .
Phương pháp giải:
- Tìm tập xác định (TXĐ) D của hàm số
- Giả sử với (). Xét hiệu
+ Nếu hay thì hàm số đồng biến trên D.
+ Nếu hay thì hàm số nghịch biến trên D.
Lời giải:
Xét hàm số
Với hai số và thuộc , ta có:
Nếu thì
Khi đó:
Suy ra:
Vậy hàm số đồng biến trên .
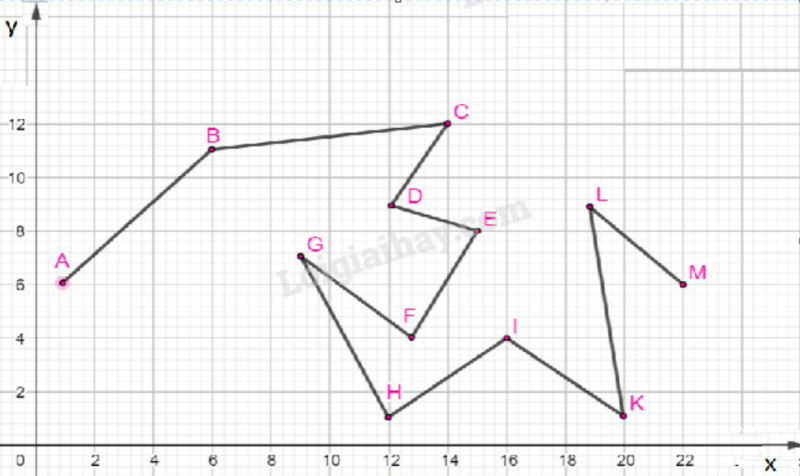
A(1; 6); B(6; 11); C(14; 12); D(12; 9);
E(15; 8); F(13; 4); G(9; 7); H(12; 1);
I(16; 4); K(20; 1); L(19; 9); M(22; 6).
Phương pháp giải:
Biểu diễn các điểm trên cùng một hệ trục tọa độ rồi nối chúng lại với nhau theo yêu cầu bài toán.
Lời giải:
Dựng hệ trục tọa độ , rồi dựng các điểm theo tọa độ của chúng, nối theo thứ tự các điểm , ta được một đường gấp khúc như hình dưới:
Bài tập bổ sung (trang 61 SBT Toán 9):
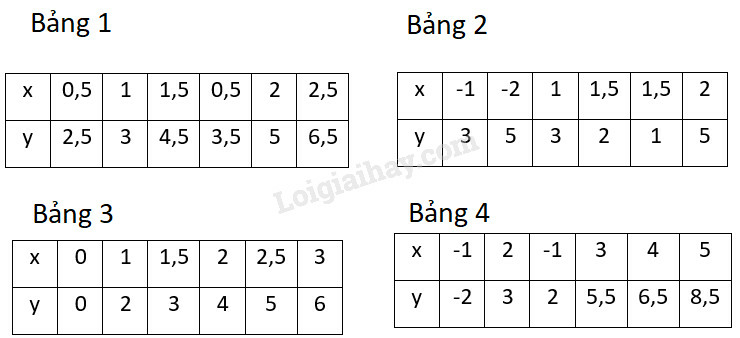
Trong các bảng trên đây, bảng xác định là hàm số của là:
(A) Bảng 1; (B) Bảng 2;
(C) Bảng 3; (D) Bảng 4.
Phương pháp giải:
- Nếu đại lượng phụ thuộc vào đại lượng thay đổi sao cho với mỗi giá trị ta luôn xác định được chỉ một giá trị tương ứng của thì được gọi là hàm số của , được gọi là biến số.
- Hàm số có thể cho bằng bảng hoặc bằng công thức.
- Giá trị của tại kí hiệu là
Lời giải:
Áp dụng định nghĩa của hàm số thì đáp án (C) đúng.
Đáp án A sai vì với có 2 giá trị của là và
Đáp án B sai vì với có 2 giá trị của là và
Đáp án D sai vì với có 2 giá trị của là và