Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số chọn lọc, có đáp án. Tài liệu có 10 trang gồm 29 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Nhắc lại và bổ sung các khái niệm về hàm số có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.
Giới thiệu về tài liệu:
- Số trang: 10 trang
- Số câu hỏi trắc nghiệm: 29 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Nhắc lại và bổ sung các khái niệm về hàm số có đáp án – Toán lớp 9:
Nhắc lại và bổ sung các khái niệm về hàm số
Câu 1: Cho hàm số y = f(x) xác định trên D. Với x1, x2 ∈ D; x1 < x2, khẳng định nào sau đây là đúng?
A. f(x1) < f(x2) thì hàm số đồng biến trên D
B. f(x1) < f(x2) thì hàm số nghịch biến trên D
C. f(x1) > f(x2) thì hàm số đồng biến trên D
D. f(x1) = f(x2) thì hàm số đồng biến trên D
Lời giải:
Cho hàm số y = f(x) xác định trên tập D. Khi đó:
- Hàm số đồng biến trên D ⇔ x1; x2 ∈ D; x1 < x2 ⇒ f(x1) < f(x2).
- Hàm số nghịch biến trên D ⇔ x1; x2 ∈ D; x1 < x2 ⇒ f(x1) > f(x2).
Đáp án cần chọn là: A
Câu 2: Cho hàm số y = f(x) xác định trên D. Với x1, x2 ∈ D; x1 > x2, khẳng định nào sau đây là đúng?
A. f(x1) < f(x2) thì hàm số đồng biến trên D
B. f(x1) > f(x2) thì hàm số nghịch biến trên D
C. f(x1) > f(x2) thì hàm số đồng biến trên D
D. f(x1) = f(x2) thì hàm số đồng biến trên D
Lời giải:
Cho hàm số y = f(x) xác định trên tập D. Khi đó:
- Hàm số đồng biến trên D ⇔ x1; x2 ∈ D; x1 > x2 ⇒ f(x1) > f(x2).
- Hàm số nghịch biến trên D ⇔ x1; x2 ∈ D; x1 > x2 ⇒ f(x1) < f(x2).
Đáp án cần chọn là: C
Câu 3: Cho hàm số f(x) = 3 – x2. Tính f(−1).
A. −2
B. 2
C. 1
D. 0
Lời giải:
Thay x = −1 vào hàm số ta được: f(−1) = 3 – (−1)2 = 2
Đáp án cần chọn là: B
Câu 4: Cho hàm số f(x) = x3 + x. Tính f(2).
A. 4
B. 6
C. 8
D. 10
Lời giải:
Thay x = 2 vào hàm số ta được: f(2) = 23 + 2 = 10
Đáp án cần chọn là: D
Câu 5: Cho hàm số f(x) = x3 − 3x – 2. Tính 2.f(3)
A. 16
B. 8
C. 32
D. 64
Lời giải:
Thay x = 3 vào hàm số ta được f(3) = 32 – 3.3 – 2 = 16 ⇒ 2. f(3) = 2.16 = 32
Đáp án cần chọn là: C
Câu 6: Cho hàm số f(x) = 3x2 + 2x + 1. Tính f(3) – 2f(2).
A. 34
B. 17
C. 20
D. 0
Lời giải:
Thay x = 3 vào hàm số ta được: f(3) = 3.32 + 2.3 + 1 = 34
Thay x = 2 vào hàm số ta được: f(2) = 3.22 + 2.2 + 1 = 17
Suy ra f(3) – 2f(2) = 34 −2.17 = 0
Đáp án cần chọn là: D
Câu 7: Cho hai hàm số f(x) = −2x3 và h(x) = 10 – 3x. So sánh f(−2) và h(−1)
A. f(−2) < h(−1)
B. f(−2) h(−1)
C. f(−2) = h(−1)
D. f(−2) > h(−1)
Lời giải:
Thay x = −2 vào hàm số f(x) = −2x3 ta được f(−2) = −2.(−2)3 = 16
Thay x = −1 vào hàm số h(x) = 10 – 3x ta được h(−1) = 10 – 3 (−1) = 13
Nên f(−2) > h(−1)
Đáp án cần chọn là: D
Câu 8: Cho hai hàm số f(x) = 6x4 và 
Lời giải:
Thay x = −1 vào hàm số f(x) = 6x4 ta được f(−1) = 6. (−1)4 = 6
Đáp án cần chọn là: A
Câu 9: Cho hai hàm số f(x) = x2 g(x) = 5x – 4. Có bao nhiêu giá trị của a để f(a) = g(a)
A. 0
B. 1
C. 2
D. 3
Lời giải:
Thay x = a vào hai hàm số đã cho ta được f(a) = a2, g(a) = 5a – 4. Khi đó:
Vậy có hai giá trị của a thỏa mãn yêu cầu đề bài.
Đáp án cần chọn là: C
Câu 10: Cho hai hàm số f(x) = −2x2 và g(x) = 3x + 5. Giá trị nào của a để 
A. a = 0
B. a = 1
C. a = 2
D. Không tồn tại
Lời giải:
Thay x = a vào hai hàm số đã cho ta được f(a) = −2a2, g(a) = 3a + 5. Khi đó
Vậy không có giá trị của a thỏa mãn yêu cầu của đề bài.
Đáp án cần chọn là: D
Câu 11: Cho hai hàm số f(x) = 2x2 và g(x) = 4x – 2. Có bao nhiêu giá trị của a để f(a) = g(a)
A. 0
B. 1
C. 2
D. 3
Lời giải:
Thay x = a vào hai hàm số ta được f(a) = 2a2, g(a) = 4a – 2
Khi đó:
Vậy có một giá trị của a thỏa mãn yêu cầu đề bài.
Đáp án cần chọn là: B
Câu 12: Cho hàm số f(x) = 5,5x có đồ thị (C). Điểm nào sau đây thuộc đồ thị hàm số (C).
A. M (0; 1)
B. N (2; 11)
C. P (−2; 11)
D. P (−2; 12)
Lời giải:
Lần lượt thay tọa độ các điểm M, N, P, Q vào hàm số f(x) = 5,5x ta được:
+) Với M (0; 1), thay x = 0; y = 1 ta được 1 = 5,5.0 ⇔ 1 = 0 (Vô lý) nên M ∉ (C)
+) Với N (2; 11), thay x = 2; y = 11 ta được 2.5,5 = 11 ⇔ 11 = 11 (luôn đúng) nên N ∈ (C)
+ Với P (−2; 11), thay x = −2; y = 11 ta được 11 = 5,5.(−2) ⇔ 11 = −11 (vô lý) nên P ∉ (C)
+) Với Q (−2; 12), thay x = −2; y = 12 ta được 12 = 5,5.(−2) ⇔ 12 = −11 (vô lý) nên Q ∉ (C)
Đáp án cần chọn là: B
Câu 13: Cho hàm số f(x) = 3x – 2 có đồ thị (C). Điểm nào sau đây thuộc đồ thị hàm số (C).
A. M (0; 1)
B. N (2; 3)
C. P (−2; −8)
D. Q (−2; 0)
Lời giải:
Lần lượt thay tọa độ các điểm M, N, P, Q vào hàm số f(x) = 3x – 2 ta được:
+) Với M (0; 1); thay x = 0; y = 1 ta được 1 = 3.0 – 2 ⇔ 1 = −2 (vô lý) nên M ∉ (C)
+) Với N (2; 3), thay x =2; y = 3 ta được 3 = 3.2 – 2 ⇔ 3 = 4 (vô lý) nên N ∉ (C)
+) Với P (−2; −8), thay x = −2; y = −8 ta được −8 = 3. (−2) – 2 ⇔ −8 = −8 (luôn đúng) nên P ∈ (C)
+ ) Với Q (−2; 0), thay x = −2; y = 0 ta được 0 = 3. (−2) – 2 ⇔ 0 = −8 (vô lý) nên Q ∉ (C)
Đáp án cần chọn là: C
Câu 14: Cho hàm số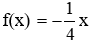 
có đồ thị (C) và các điểm M (0; 4); P (4; −1); Q (−4; 1); A (8; −2); O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C).
A. 4
B. 3
C. 2
D. 1
Lời giải:
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số 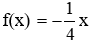ta được:
Vậy có bốn điểm thuộc đồ thị (C) trong số các điểm đã cho.
Đáp án cần chọn là: A
Câu 15: Cho hàm số f(x) = 3x có đồ thị (C) và các điểm M (1; 1); P (−1; −3); Q (3; 9); A (−2; 6); O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C).
A. 4
B. 3
C. 2
D. 1
Lời giải:
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f(x) = 3x ta được:
+) Với M (1; 1), thay x = 1; y = 1 ta được 1 = 3.1 ⇔ 1 = 3 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0; y = 0 ta được 0 = 3.0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (−1; −3), thay x = −1; y = −3 ta được −3 = 3.(−1) ⇔ −3 = −3 (luôn đúng) nên P (C)
+) Với Q (3; 9), thay x = 3; y = 9 ta được 9 = 3.3 ⇔ 9 = 9 (luôn đúng) nên Q ∈ (C)
+) Với M (−2; 6), thay x = −2; y = 6 ta được 6 = 3.(−2) ⇔ 6 = −6 (vô lý) nên A ∉ (C)
Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.
Đáp án cần chọn là: B
Câu 16: Đường thẳng nào sau đây đi qua điểm M (1; 4)?
A. 2x + y – 3 = 0
B. y – 5 = 0
C. 4x – y = 0
D. 5x + 3y – 1 = 0
Lời giải:
+) Thay x = 1; y = 4 vào 2x + y – 3 = 0 ta được 2.1 + 4 – 3 = 3 ≠ 0
+) Thay x = 1; y = 4 vào y – 5 = 0 ta được 4 – 5 = −1 ≠ 0
+) Thay x = 1; y = 4 vào 4x – y = 0 ta được 4.1 – 4 = 0
+) Thay x = 1; y = 4 vào 5x + 3y – 1 = 0 ta được 5.1 + 3.4 – 1 = 16 ≠ 0
Vậy đường thẳng d: 4x – y = 0 đi qua M (1; 4)
Đáp án cần chọn là: C
Câu 17: Đường thẳng nào sau đây đi qua điểm N (1; 1)
A. 2x + y – 3 = 0
B. y – 3 = 0
C. 4x + 2y = 0
D. 5x + 3y – 1 = 0
Lời giải:
+) Thay x = 1; y = 1 vào 2x + y – 3 = 0 ta được 2.1 + 1 – 3 = 3 = 0 Nên điểm N thuộc đường thẳng 2x + y – 3 = 0
+) Thay x = 1; y = 1 vào y – 3 = 0 ta được 1 – 3 = −2 ≠ 0
+) Thay x = 1; y = 1 vào 4x + 2y = 0 ta được 4.1 + 2.1 = 6 ≠ 0
+) Thay x = 1; y = 1 vào 5x + 3y – 1 = 0 ta được 5.1 + 3.1 −1 = 7 ≠ 0
Vậy đường thẳng d: 2x + y – 3 = 0 đi qua N (1; 1)
Đáp án cần chọn là: A
Câu 18: Hàm số y = 1 – 4x là hàm số?
A. Đồng biến
B. Hàm hằng
C. Nghịch biến
D. Đồng biến với x > 0
Lời giải:
TXĐ: D = R
Giả sử x1 < x2 ∈ R và x1, x2 . Ta có f(x1) = 1 – 4x1; f(x2) = 1 – 4x2.
Xét hiệu H = f(x1) – f(x2) = 1 – 4x1 – (1 – 4x2) = 1 – 4x1 – 1 + 4x2 = 4(x2 – x1) > 0 (vì x1 < x2)
Vậy y = 1 – 4x là hàm nghịch biến.
Đáp án cần chọn là: C
Câu 19: Hàm số y = 5 – 3x là hàm số?
A. Nghịch biến
B. Hàm hằng
C. Đồng biến
D. Đồng biến với x > 0
Lời giải:
TXĐ: D = R
Giả sử x1 < x2 ∈ R và x1, x2 . Ta có f(x1) = 5 – 3x1; f(x2) = 5 – 3x2.
Xét hiệu H = f(x1) – f(x2) = 5 – 3x1 – (5 – 3x2) = 5 – 3x1 – 5 + 3x2 = 3(x2 – x1) > 0 (vì x1 < x2)
Vậy y = 5 – 3x là hàm nghịch biến.
Đáp án cần chọn là: A
Câu 20: Hàm số y = 5x – 16 là hàm số?
A. Đồng biến
B. Hàm hằng
C. Nghịch biến
D. Nghịch biến với x > 0
Lời giải:
TXĐ: D = R
Giả sử x1 < x2 ∈ R và x1, x2 . Ta có f(x1) = 5x1 – 16; f(x2) = 5x2 – 16.
Xét hiệu H = f(x1) – f(x2) = 5x1 – 16 – (5x2 – 16) = 5x1 – 16 – 5x2 + 16 = 5(x1 – x2) < 0 (vì x1 < x2)
Vậy y = 5x – 16 là hàm số đồng biến.
Đáp án cần chọn là: A
Câu 21: Hàm số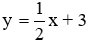 
là hàm số?
A. Hàm hằng
B. Đồng biến
C. Nghịch biến
D. Nghịch biến với x > 0
Lời giải:
Đáp án cần chọn là: B
Câu 22: Cho hàm số y = (3m – 2)x + 5m. Tìm m để hàm số nhận giá trị là 2 khi x = −1
A. m = 0
B. m = 1
C. m = 2
D. m = −1
Lời giải:
Thay x = −1; y = 2 vào y = (3m – 2)x + 5m ta được 2 = (3m – 2).(−1) + 5m
⇔ 2m = 0 ⇔ m = 0
Đáp án cần chọn là: A
Câu 23: Cho hàm số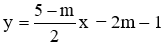 
. Tìm m để hàm số nhận giá trị là −5 khi x = 2.
A. m = 5
B. m = 3
C. m = 2
D. m = −3
Lời giải:
Thay x = 2; y = −5 vào 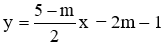ta được
Đáp án cần chọn là: B
Câu 24: Cho hàm số y = mx – 3m + 2. Tìm m để đồ thị hàm số đi qua điểm A (2; −3)
A. m = 3
B. m = 4
C. m = 5
D. m = 6
Lời giải:
Thay x = 2; y = −3 vào y = mx – 3m + 2 ta được
m.2 – 3m + 2 = −3 ⇔ −m = −5 ⇔ m = 5
Đáp án cần chọn là: C
Câu 25: Cho hàm số y = (2 – 3m)x – 6. Tìm m để đồ thị hàm số đi qua điểm A (−3; 6)
A. m = 3
B. m = 4
C. m = 9
D. m = 2
Lời giải:
Thay x = −3; y = 6 vào y = (2 – 3m)x – 6 ta được 6 = (2 – 3m).(−3) – 6
⇔ 9m = 18 ⇔ m = 2
Đáp án cần chọn là: D
Câu 26: Cho hàm số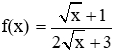 
. Tính f(a2) với a < 0.
Lời giải:
Đáp án cần chọn là: D
Câu 27: Cho hàm số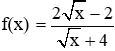 
. Tính f(4a2) với a ≥ 0
Lời giải:
Đáp án cần chọn là: A
Câu 28: Cho hàm số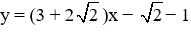 
. Tìm x để y = 0.
Lời giải:
Đáp án cần chọn là: D
Câu 29: Cho hàm số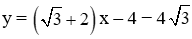 
. Tìm x để y = 3.
Lời giải:
Đáp án cần chọn là: C
Bài giảng Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
