Tailieumoi.vn giới thiệu Giải bài tập Toán 9 Bài 3: Bảng lượng giác chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Bảng lượng giác 9.
Giải bài tập Toán 9 Bài 3: Bảng lượng giác
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 80 SGK Toán 9 Tập 1:Sử dụng bảng, tìm cot47o24’
Lời giải:
cot47o24’ = 0,9195
Phương pháp giải:
Sử dụng bảng lượng giác
Lời giải:
tg82013'≈7,316
Trả lời câu hỏi 3 trang 81 SGK Toán 9 Tập 1 :Sử dụng bảng tìm góc nhọn , biết
Lời giải:
Phương pháp giải:
Sử dụng bảng lượng giác
Lời giải:
.
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
+) Sử dụng bảng lượng giác hoặc dùng máy tính bỏ túi để bấm các tỉ số lượng giác.
+) Dùng quy tắc làm tròn để làm tròn đến chữ số thập phân thứ tư.
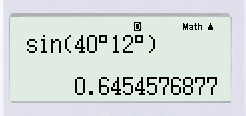
b) ;
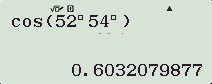
c) ;
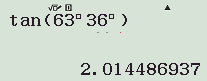
d) .
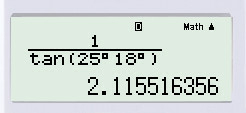
Nhận xét: Vì trong máy tính không có phím cotg nên để tìm ta phải tìm rồi lấy nghịch đảo của kết quả hay ta bấm luôn như trên.
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
a) . Dùng máy tính lần lượt bấm các phím:

d) ) Từ công thức Biết , tính được . Dùng máy tính tính được góc . Dùng máy tính bấm lần lượt các phím sau:

Lời giải:
a) ;
Cách bấm máy:
![]()
b) ;
Cách bấm máy:
![]()
c) ;
Cách bấm máy:
![]()
d) .
Cách bấm máy:
![]()
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
+) Thực hiện bấm máy tính và dùng quy tắc làm tròn số.
+) Sử dụng công thức .
Do đó để tính , ta tính sau đó nghịch đảo kết quả.
Lời giải:
a) ;
Cách bấm máy:
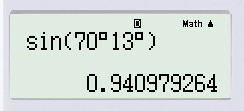
b) ;
Cách bấm máy:

c) ;
Cách bấm máy:

d) .
Cách bấm máy:
a)
b) ;
c) ;
d) .
Phương pháp giải:
a) b) c) Dùng máy tính bỏ túi
d) Sử dụng công thức .
Biết tính được từ đó tìm được góc .
Lời giải:
a) ;
Cách bấm máy:
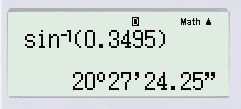
b) ;
Cách bấm máy:
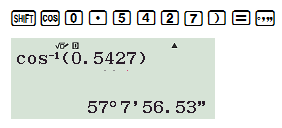
c) ;
Cách bấm máy:

d) .
Cách bấm máy:
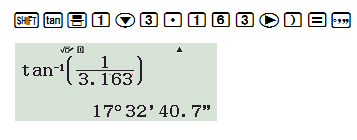
a) và
b) và
c) và
d) và
Phương pháp giải:
Nếu thì:
+)
+) .
+) .
+) .
Lời giải:
a) Vì nên (góc tăng, sin tăng)
b) Vì nên (góc tăng, cos giảm)
c) Vì nên (góc tăng, tan tăng)
d) Vì nên (góc tăng, cot giảm )
Chú ý sai lầm: Một số bạn từ ở câu b suy ra là sai vì khi góc tăng từ đến thì giảm.
a)
b)
Phương pháp giải:
a) Dùng công thức hai góc phụ nhau: Nếu thì để đưa về cùng .
b) Dùng công thức hai góc phụ nhau: Nếu thì để đưa về cùng .
Lời giải:
a) Ta có: .
b) Ta có:
Nhận xét: Cách giải như trên là dựa vào định lý: nếu hai góc phụ nhau thì sin của góc này bằng côsin của góc kia, tang của góc này bằng côtang của góc kia.
a) ;
b) .
Phương pháp giải:
a) +) Sử dụng công thức để đưa hết về cùng là của một góc.
+) Nếu , với .
b) +) Sử dụng công thức để đưa hết về cùng là của một góc.
+) Nếu , với .
Lời giải:
a) Ta có: ;
Vì
.
b) Ta có:
.
Vì
;
a) và .
b) và ;
c) và ;
d) và .
Phương pháp giải:
+) Sử dụng các công thức định nghĩa tỉ số lượng giác. Chú ý rằng với .
+) Sử dụng công thức tỉ số lượng giác của hai góc phụ nhau: nếu thì:
; .
Lời giải:
a) Ta có ( do
b) Ta có: ( do
c)
Cách 1:
Ta có
Cách 2:
Ta có ( do
Mà
Vậy .
d) Cách 1:
Ta có
Cách 2:
Ta có: ( do
Mà
Do đó .
Chú ý:
Với các góc đặc biệt, ta có thể tính tỉ số lượng giác của chúng rồi so sánh
1. Cấu tạo của bảng lượng giác
- Bảng sin và côsin (Bảng VIII)
- Bảng tang và côtang (Bảng IX)
- Bảng tang của các góc gần 90° (Bảng X)
Nhận xét:
Khi góc α tăng từ 0° đến 90° (0°<α < 90°) thì sinα và tgα tăng còn cosα và cotgα giảm.
2. Cách dùng bảng, dùng máy tính:
a) Tìm tỉ số lượng giác của một góc nhọn cho trước.
b) Tìm số đo của góc nhọn khi biết một tỷ số lượng giác của góc đó.