Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 10 Bài 5: Phương trình đường tròn sách Cánh diều. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 10.
Trắc nghiệm Toán 10 Bài 5: Phương trình đường tròn
Câu 1. Đường tròn có tâm trùng với gốc tọa độ, bán kính R = 1 có phương trình là:
A.
B.
C.
D.
Đáp án đúng là: B
Đường tròn (C) phải thoả mãn hai điều kiện sau:
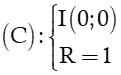
Câu 2. Đường tròn có tâm I (1; 2), bán kính R = 2 có phương trình là:
A. x2 + y2 – 2x – 4y + 1 = 0;
B. x2 + y2 + 2x – 4y – 4 = 0;
C. x2 + y2 – 2x + 4y – 4 = 0;
D. x2 + y2 – 2x – 4y – 4 = 0
Đáp án đúng là: A
Đường tròn có tâm I (1; 2), bán kính R = 2 có phương trình là:
(x – 1)2 + (y – 2)2 = 4
⇔ x2 + y2 – 2x – 4y + 1 = 0
Câu 3. Đường tròn (C)đi qua ba điểm A (– 1; – 2), B(0; 1) và C(1; 2) có phương trình là:
A. (x – 4)2 + (y – 2)2 = 52;
B. (x – 4)2 + (y + 2)2 = 52;
C. (x + 4)2 + (y + 2)2 = 52;
D. (x + 4)2 + (y – 2)2 = 52.
Đáp án đúng là: B
Gọi phương trình đường tròn cần tím có dạng (C): x2 + y2 + 2ax + 2by + c = 0.
Vì (C) đi qua các điểm A, B, C nên lần lượt thay tọa độ các điểm vào phương trình (C) ta được hệ phương trình:
Vậy phương trình đường tròn (C) là x2 + y2 – 8x + 4y – 5 = 0 ⇔ (x – 4)2 + (y + 2)2 = 52.
Câu 4. Đường tròn (C) có tâm I (– 2; 3) và đi qua M (2; – 3) có phương trình là:
A.
B.
C.
D.
Đáp án đúng là: D
Ta có: Bán kính của đường tròn:
R = IM =
Vậy phương trình đường tròn 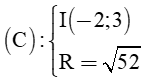
hay x2 + y2 + 4x – 6y – 39 = 0.
Câu 5. Đường tròn đường kính AB với A (3; – 1), B (1; – 5) có phương trình là:
A. (x + 2)2 + (y – 3)2 = 5;
B. (x + 1)2 + (y + 2)2 = 17;
C. (x – 2)2 + (y + 3)2 = ;
D. (x – 2)2 + (y + 3)2 = 5;
Đáp án đúng là: D
Ta có: Bán kính của đường tròn là:
R = = =
Khi đó phương trình đường tròn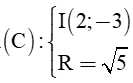
(C): (x – 2)2 + (y + 3)2 = 5.
Câu 6. Tọa độ tâm I và bán kính R của đường tròn là:
A. I (– 1; 3), R = 4;
B. I (1; – 3), R = 5;
C. I (1; – 3), R = 16;
D. I (– 1; 3), R = 16.
Đáp án đúng là: B
Ta có:
Tâm I (1; – 3), bán kính R == 5.
Câu 7.Cho đường tròn có tọa độ tâm I(a; b) và bán kính R = c. Nhận xét nào sau đây đúng về a, b và c:
A. a + b = c;
B. a + b = – 2c;
C. a – 2b = c;
D.a – 2b = – 2c.
Đáp án đúng là: B
Ta có:
I (0; – 4); = 2.
⇒ a = 0, b = – 4, c = 2
Khi đó ta có nhận xét: a + b = 0 + (– 4) = – 4 = – 2c.
Câu 8.Cho phương trình x2 + y2 – 2ax – 2by + c = 0. Điều kiện của a, b, c để phương trình đã cho là phương trình đường tròn:
A. a2 + b2 > c2;
B. c2 > a2 + b2;
C. a2 + b2 > c;
D. c > a2 + b2.
Đáp án đúng là: C
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn khi a2 + b2 > c.
Câu 9. Tọa độ tâm I và bán kính R của đường tròn (C): x2 + y2 = 16 là:
A. I (0; 0), R = 9;
B. I (0; 0), R = 81;
C. I (1; 1), R = 3;
D. I (0; 0), R = 4;
Đáp án đúng là: D
Ta có:(C): x2 + y2 = 16
I (0; 0); R = = 4.
Câu 10. Đường tròn (C): x2 + y2 – 8x + 2y + 6 = 0 có tâm I, bán kính R lần lượt là:
A. I (3; – 1), R = 4;
B. I (– 3; 1), R = 4;
C. I (4; – 1), R = ;
D. I (– 3; 1), R = 2.
Đáp án đúng là: C
Ta có:(C): x2 + y2 – 8x + 2y + 6 = 0⇔ x2 + y2 – 2.4x – 2.(– 1)y + 6 = 0
⇒a = 4; b = – 1 và c = 6
⇒I (4; – 1), .
Câu 11. Phương trình tiếp tuyến d của đường tròn (C): (x + 2)2 + (y + 2)2 = 9 tại điểm M (2; 1) là:
A. d: – y + 1 = 0;
B. d: 4x + 3y + 14 = 0;
C. d: 3x – 4y – 2 = 0;
D. d: 4x + 3y – 11 = 0.
Đáp án đúng là: D
Đường tròn (C) có tâm I (– 2; – 2) nên tiếp tuyến tại M có VTPT là nên có phương trình là: 4.(x – 2) + 3. (y – 1) = 04x + 3y –11 = 0.
Câu 12. Cho đường tròn (C): (x – 1)2 + (y + 2)2 = 2. Viết phương trình tiếp tuyến d của (C) biết đường d song song với đường thẳng d’: x + y + 3 = 0.
A. d: x + y + 1 = 0;
B. d: x –y –1 = 0;
C. d: x + y – 1 = 0;
D. d: x + y + 3 = 0.
Đáp án đúng là: C
Đường tròn (C) có tâm I (1; – 2) và bán kính R = .
Phương trình đường thẳng d // d’ nên có dạng x + y + m = 0 (m ≠ 3).
Vì d là tiếp tuyến của đường tròn (C) nên khoảng cách từ tâm I đến đường thẳng d bằng bán kính của đường tròn. Do đó ta có:
⇔ m – 1 = 2 hoặc m – 1 = – 2
⇔ m = 3 (không thỏa mãn) hoặc m = – 1 (thỏa mãn).
Vậy phương trình tiếp tuyến cần tìm là x + y – 1 = 0.
Câu 13. Phương trình tiếp tuyến d của đường tròn (C): x2 + y2 – 3x – y = 0 tại điểm N(1; – 1) là:
A. d: x + 3y – 2 = 0;
B. d: x – 3y + 4 = 0;
C. d: x – 3y – 4 = 0;
D. d: x + 3y + 2 = 0.
Đáp án đúng là: D
Xét phương trình (C): x2 + y2 – 3x – y = 0 ⇔ .
Khi đó đường tròn (C) có tâm nên tiếp tuyến tại N có VTPT là:
Nên có phương trình là: 1(x – 1) +3(y + 1) = 0x + 3y + 2 = 0.
Câu 14. Viết phương trình tiếp tuyến của đường tròn (C): (x – 3)2 + (y + 1)2 = 5, biết tiếp tuyến song song với đường thẳng d: 2x + y + 7 = 0.
A. 2x + y + 1 = 0 hoặc 2x + y – 1 = 0;
B. 2x + y = 0 hoặc 2x + y – 10 = 0;
C. 2x + y + 10 = 0 hoặc 2x + y – 10 = 0;
D. 2x + y = 0 hoặc 2x + y + 10 = 0.
Đáp án đúng là: B
Đường tròn (C) có tâmI(3; –1), R = và tiếp tuyến có dạng : 2x + y + c = 0 (c ≠ 7)
Ta có:
Bán kính của đường tròn
suy ra::2x + y = 0 hoặc :2x + y – 10 = 0.
Câu 15. Viết phương trình tiếp tuyến của đường tròn ,
biết tiếp tuyến vuông góc đường thẳng d: 3x – 4y – 2018 = 0.
A. 3x – 4y + 39 = 0 hoặc 3x – 4y – 11 = 0;
B. 4x + 3y + 39 = 0 hoặc 3x – 4y – 11 = 0;
C. 3x – 4y + 39 = 0 hoặc 4x + 3y – 11 = 0;
D. 4x + 3y + 39 = 0 hoặc 4x + 3y – 11 = 0.
Đáp án đúng là: D
Xét phương trình đường thẳng d có VTPT là (3; – 4) suy ra VTCP của đường thẳng d là (4; 3).
Vì phương trình tiếp tuyến vuông góc với đường thẳng d nên nhận (4; 3) làm VTPT khi đó phương trình tiếp tuyến có dạng: 4x + 3y + c = 0
Ta có: Đường tròn (C) có tâm I(– 2; – 2), R = 5
Bán kính đường tròn:
Suy ra có hai phương trình tiếp tuyến thỏa mãn: 4x + 3y + 39 = 0 hoặc :4x + 3y –11 = 0.
Xem thêm các bài trắc nghiệm Toán 10 Cánh diều hay, chi tiết khác:
Trắc nghiệm Toán 10 Bài 3: Phương trình đường thẳng
Trắc nghiệm Toán 10 Bài 5: Phương trình đường tròn