Với giải Bài 97 trang 105 Toán lớp 9 chi tiết trong Ôn tập chương 3 Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài Ôn tập chương 3 Hình học

Bài 97 trang 105 SGK Toán lớp 9 Tập 2: Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:

a) ABCD là một tứ giác nội tiếp;

b) $\widehat{ABD}=\widehat{ACD}$

c) CA là tia phân giác của góc SCB.

Lời giải:

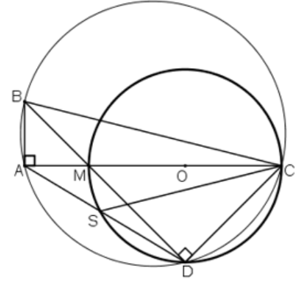
a)

Tam giác ABC vuông tại A (gt)$\Rightarrow \widehat{BAC}={90}^o$

Do đó, A thuộc đường tròn đường kính BC (1)

Mặt khác, D thuộc đường tròn đường kính MC

$\Rightarrow \widehat{BDC}=\widehat{MDC}={90}^o$

Do đó, D cũng thuộc đường tròn đường kính BC (2)

Từ (1) và (2), ta suy ra A, B, C, D cùng thuộc đường tròn đường kính BC

Do đó, tứ giác ABCD nội tiếp.

b)

Xét đường tròn đường kính BC:

Góc ABD và góc ACD đều là góc nội tiếp chắn cung AD

$\Rightarrow \widehat{ABD}=\widehat{ACD}$

c)

Xét đường tròn đường kính MC có:

Góc SCM và góc SDM đều là các góc nội tiếp cùng chắn cung SM

$$\begin{gathered} \Rightarrow \widehat{SCM}=\widehat{SDM} \\ \Rightarrow \widehat{SCM}=\widehat{ADB} \end{gathered}$$

Xét đường tròn đường kính BD có:

Góc ADB và góc ACB đều là các góc nội tiếp cùng chắn cung AB

$\Rightarrow \widehat{ADB}=\widehat{ACB}$ (2)

Từ (1) và (2) ta suy ra: $\widehat{SCM}=\widehat{ACB}$

Do đó, CA là tia phân giác của góc SCB.