Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập trắc nghiệm Góc với đường tròn Toán lớp 9, tuyển chọn 48 bài tập trắc nghiệm Góc với đường tròn, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi Tuyển sinh lớp 10 môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

CHUYÊN ĐỀ GÓC VỚI ĐƯỜNG TRÒN

A. Lý thuyết

1. Định nghĩa

- Góc có đỉnh trùng với tâm đường tròn gọi là góc ở tâm.

- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

- Số đo của cung lớn bằng trừ đi số đo của cung nhỏ.

- Số đo của nửa đường tròn bằng.

2. Trong một đường tròn hay trong hai đường tròn bằng nhau

- Hai cung bằng nhau căng hai dây bằng nhau.

- Hai dây bằng nhau căng hai cung bằng nhau.

3. Nếu C là một điểm nằm trên cung AB thì:

Sđ AB = Sđ AC + Sđ CB

4. Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Hai cung bằng nhau căng hai dây bằng nhau.

- Hai dây bằng nhau căng hai cung bằng nhau.

5. Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Cung lớn hơn căng dây lớn hơn.

- Dây lớn hơn căng cung lớn hơn.

B. Bài tập

Bài 1: Cho đường tròn (O, R) và điểm M nằm ngoài đường tròn đó. Gọi MA, MB là hai tiếp tuyến với đường tròn tại A và B. Tính số đo của góc ở tâm tạo bởi hai bán kính OA và OB nếu:

a) ∠AMB = 70^o

b) MA = R

c) MO = 2R

Hướng dẫn giải

Vì MA và MB là các tiếp tuyến của đường tròn (O) tại A và B nên: MA ⊥ OA, MB ⊥ OB

Suy ra: ∠MAO = ∠MBO = 90^o

a)

Xét tứ giác MAOB có:

∠AMB + ∠AOB + ∠MAO + ∠MBO = 360^o

⇔ ∠AOB = 360^o - (∠AMB + ∠MAO + ∠MBO)

= 360^o - (70^o+ 90^o + 90^o)

= 110^o

Vậy số đo góc ở tâm tạo bởi hai bán kính OA, OB bằng 110^o .

b)

Nếu MA = R

Xét ΔMAO có: MA = AO = R và ∠MAO = 90^o

=> Δ MAO vuông cân tại A

=> ang;MOA = 45^o

Vậy ∠AOB = 2.∠MOA = 90^o

c)

Nếu MO = 2R

Xét ΔMAO vuông tại A có: MO = 2.AO

=> ∠AMO = 30^o => ∠AOM = 60^o

Vậy: ∠AOB = 2.∠AOM = 120^o

Bài 2: Cho đường tròn (O; R) và dây AB không đi qua O. Trên dây AB lấy các điểm M, N sao cho AM = MN = NB. Tia OM, ON cắt (O) lần lượt tại C và D.

Hướng dẫn giải

Thât vậy, xét ΔAOM và ΔBON có:

OA = OB = R

∠OAM = ∠OBN (do ΔOAB cân tại O)

AM = BN (gt)

Suy ra ΔAOM = ΔBON(c-g-c)

Suy ra ∠AOM = ∠BON (hai góc tương ứng)

Gọi I là trung điểm của OB. Suy ra NI là đường trung bình của ΔOBM nên NI // OM => ∠MON = ∠ONI(so le trong) (1)

Mặt khác ta có: OB = OC = R, mà M ∈ OC => OM < OB hay NI < OI.

Xét ΔONI có NI < OI nên: ∠NOI < ∠ONI (2)

Từ (1) và (2) suy ra ∠NOI < ∠MON

Bài 3: Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại A và B. Kẻ dây AM của đường tròn (O) và dây BN của đường tròn (O’) sao cho AM // BN.

Hướng dẫn giải

Vì AM // BN (gt) => ∠MAB = ∠ABN (so le trong) (1)

Mặt khác: OA = OB = O'A = O'B nên tứ giác OAO’B là hình thoi, do đó ∠OAB = ∠ABO' (2)

Từ (1) và (2) suy ra: ∠MAO = ∠NBO'

Ta có: ΔMOA cân tại O và ΔNO'B cân tại O' có góc ở đáy bằng nhau nên ∠MOA = ∠NO'B

Do đó: ΔMOA = ΔNO'B(c.g.c) => AM = BN

Mặt khác hai đường tròn (O) và (O”) bằng nhau nên

Bài 4: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm A và B (R < R'). Kẻ đường kính BOC và BO’D.

a) Chứng minh rằng: Ba điểm C, A, D thẳng hàng.

b) So sánh số đo hai cung nhỏ AC và AD.

Hướng dẫn giải

a) Vì ΔABC nội tiếp đường tròn đường kính BC nên ΔABC vuông tại A hay ∠BAC = 90^o .

Tương tự ta có: ∠BAD = 90^o

Suy ra: ∠CAD = ∠BAD + ∠BAC = 180^o nên 3 điểm C, A, D thẳng hàng.

b) Xét đường tròn (O) có:

Xét đường tròn (O’) có:

Từ đó suy ra

Bài 5: Cho đường tròn (O) đường kính AB. Điểm C thuộc đường tròn (O) sao cho SđBC = 30^o, điểm M thuộc cung AC nhỏ. Gọi D và E là các điểm đối xứng với M qua AB và OC. Chứng minh rằng: ΔDOE đều.

Hướng dẫn giải

Vì SđBC = 30^o => ∠BOC = 30^o

Gọi I là giao điểm của MD và AB, J là giao điểm của ME và OC.

Theo giả thiết: M và D đối xứng với nhau qua AB, mà M thuộc đường tròn (O) nên D cũng thuộc đường tròn (O). Tương tự E thuộc đường tròn (O).

Tứ giác MIOJ có ∠I = ∠J = 90^o

=> ∠IMJ + ∠IOJ = 180^o

=> ∠IMJ = 180^o - ∠IOJ = ∠BOC = 30^o

Ta có ΔMOD và ΔMOE cân tại O nên:

∠MOD = 180^o - 2∠DMO

∠MOE = 180^o - 2∠EMO

=> ∠MOD + ∠MOE = 360^o - 2(∠DMO + ∠EMO)

⇔ 360^o - ∠DOE = 360^o - ∠IMJ

⇔ ∠DOE = 2∠IMJ = 60^o

Vậy ΔDOE đều.

Bài 6: Cho điểm M chuyển động trên nửa đường tròn (O) đường kính AB. Vẽ hai tiếp tuyến Ax và By với đường tròn (O). Tiếp tuyến tại M với (O) cắt Ax tại C và cắt By tại D; các đường thẳng CO và OD cắt (O) lần lượt tại E và F.

a) Tính Sđ EF.

b) Tìm tập hợp tâm I của đường tròn ngoại tiếp .

Hướng dẫn giải

a) Vì CA và BM là hai tiếp tuyến với (O) nên OC là tia phân giác của ∠AOM .

Tương tự ta có OD là tia phân giác của ∠BOM

Mà ∠AOM và ∠BOM là hai góc kề bù, suy ra OC ⊥ OD

Vậy ta có ∠COD = 90^o hay SđEF = 90^o .

b) * Phần thuận:

Vì ΔCOD vuông tại O nên tâm I của đường tròn ngoại tiếp tam giác ΔCOD là trung điểm của CD.

Dễ thấy tứ giác ABCD là hình thang có OI là đường trung bình nên OI//AC => OI ⊥ AB.

Vậy I chuyển động trên đường thẳng d vuông góc với AB tại O.

* Phần đảo và giới hạn: Học sinh tự chứng minh.

Bài 7: Cho AB là dây cung của đường tròn (O), I là trung điểm của AB. Trên cung nhỏ AB lấy điểm M tùy ý. Gọi giao điểm OI và MI với (O) lần lượt C và N. 

Hướng dẫn giải

Kẻ OH ⊥ MN

Ta có: ΔOHI vuông tại H nên OH < OI.

Mà OH, OI lần lượt là các khoảng cách từ O đến hai dây MN và AB nên suy ra AB < MN. Do đó

Bài 8: Cho ΔABC đều. Vẽ nửa đường tròn tâm O đường kính BC ra phía ngoài ΔABC. Gọi D và E là hai điểm thuộc nửa đường tròn sao cho cungBD = cungDE = cungEC . AD và AE cắt BC lần lượt tại M và N. Chứng minh rằng:

a) ΔABN ∼ ΔECN

b) BM = MN = NC

Hướng dẫn giải

b) Vì ΔABC và ΔOCE là hai tam giác đều có BC = 2OC nên suy ra AB = 2CE.

Lại có: ΔABN ∼ ΔECN (chứng minh a)

⇔ BN = 2NC do đó: BM = MN = NC.

Bài 9: Qua điểm M nằm ngoài đường tròn (O), vẽ hai cát tuyến MAB và MCD với đường tròn sao cho AB > CD. Gọi H và K lần lượt là trung điểm của AB và CD. Chứng minh rằng:

a) MH > MK

b) ∠MOH > ∠MOK

Hướng dẫn giải

a) Vì H, K lần lượt là trung điểm của AB, CD nên OH ⊥ AB, OK ⊥ CD (quan hệ giữa đường kính và dây cung).

Ta có: AB > CD => OH < OK (liên hệ giữa dây cung và khoảng cách đến tâm).

=> MH > MK

Vì ∠MHO = ∠MKO = 90^o nên H, K cùng thuộc đường tròn đường kính MO.

Trong đường tròn đường kính MO, ta có MH > MK

Mặt khác: ∠MOH = 1/2 SđMH

∠MOK = 1/2 SđMK

Từ đó suy ra: ∠MOH > ∠MOK .

Bài 10: Trên đường tròn (O; R), lấy lần lượt theo cùng một chiều các điểm A, B, C, D sao cho

Chứng minh rằng S_ΔAOB = S_ΔCOD .

Hướng dẫn giải

Kéo dài OC cắt đường tròn (O) tại E.

Do đó: ΔAOB = ΔEOD nên S_ΔAOD = S_ΔEOD (1)

Mặt khác: ΔEOD và ΔCOD có chung chiều cao kẻ từ D xuống EC và độ dài hai đáy EO = OC nên S_ΔEOD = S_ΔCOD (2)

Từ (1) và (2) suy ra: S_ΔAOB = S_ΔCOD .

Bài 11: Tâm đường tròn ngoại tiếp tam giác là:

A. Giao điểm 3 đường phân giác của tam giác       

B. Giao điểm 3 đường cao của tam giác

C. Giao điểm 3 đường trung tuyến của tam giác    

D. Giao điểm 3 đường trung trực của tam giác

Bài 12: Đường tròn tâm A có bán kính 3cm là tập hợp các điểm:

A. Có khoảng cách đến điểm A nhỏ hơn hoặc bằng 3cm.

B. Có khoảng cách đến A bằng 3cm.

C. Cách đều A.

D. Có hai câu đúng.

Bài 13: Cho DABC nội tiếp đường tròn tâm O. Biết $\hat{A}=50°$ ; $\hat{B}=65°$. Kẻ OH $\perp$ AB; OI $\perp$ AC ; OK $\perp$BC. So sánh OH, OI, OK ta có:

A. OH = OI = OK     

B. OH = OI > OK

C. OH = OI < OK     

D. Một kết quả khác

Bài 14: Trong hình bên, biết BC = 8cm; OB = 5cm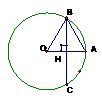

Độ dài AB bằng:

A. 20 cm     

B. $\sqrt{6}$ cm

C. $2\sqrt{5}$ cm   

D. Một kết quả khác

Bài 15: Cho đường tròn (O ; R) và dây AB = R$\sqrt{3}$, Ax là tia tiếp tuyến tại A của đường tròn (O). Số đo của $\widehat{xAB}$ là:

A. 90⁰   

B. 120⁰

C. 60⁰   

D. B và C đúng

Bài 16: Cho đường tròn (O ; R) và điểm A bên ngoài đường tròn. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) và cát tuyến AMN đến (O). Trong các kết luận sau kết luận nào đúng:

A. AM. AN = 2R²   

B. AB² = AM. MN

C. AO² = AM. AN 

D. AM. AN = AO²  R²

Bài 17: Cho tứ giác ABCD nội tiếp đường tròn (O). Biết $\widehat{BOD}=124°$thì số đo $\widehat{BAD}$ là:

A. 56⁰ 

B. 118⁰ 

C. 124⁰   

D. 64⁰

Bài 18: Cho hai đường tròn (O ; 4cm) và (O' ; 3cm) có OO' = 5cm. Hai đường tròn trên cắt nhau tại A và B. Độ dài AB bằng:

A. 2,4cm   

B. 4,8cm   

C. $\frac{5}{12}$cm 

D. 5cm

Bài 19: Cho đường tròn (O ; 2cm). Từ điểm A sao cho OA = 4cm vẽ hia tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Chu vi $△$ABC bằng:

A. $6\sqrt{3}$cm   

B. $5\sqrt{3}$cm

C. $4\sqrt{3}$cm   

D.$2\sqrt{3}$ cm