Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Góc và đường tròn Toán lớp 9, tài liệu bao gồm 4 trang, tuyển chọn 15 bài tập Góc và đường tròn đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi Tuyển sinh lớp 10 môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Lý thuyết, bài tập về Góc và đường tròn gồm các nội dung sau:
A. Lý thuyết Chương 3 Hình học: Góc với đường tròn
1. Góc ở tâm
Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.
+ Hai cạnh của góc ở tâm cắt đường tròn tại hai điểm, do đó chia đường tròn thành hai cung.
⋅ Với các góc α ( 0 < α < 180°) thì cung nằm bên trong góc được gọi là cung nhỏ.
⋅ Cung nằm bên ngoài góc được gọi là cung lớn.
2. Số đo góc.
+ Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu giữa 360° và số đo cung nhỏ (có chung hai mút với cung lớn).
+ Số đo của nửa đường tròn bằng 180°
+ Kí hiệu số đo của cung AB là sđ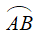 
.
3. Liện hệ giữa cung và dây
a) Định lí 1
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+ Hai cung bằng nhau căng hai dây bằng nhau.
+ Hai dây bằng nhau căng hai cung bằng nhau.
b) Định lí 2
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+ Cung lớn hơn căng dây lớn hơn.
+ Dây lớn hơn căng cung lớn hơn.
c) Mở rộng
+ Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
+ Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
4. Góc nội tiếp
a) Định nghĩa
+ Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
+ Cung nằm bên trong góc được gọi là cung bị chắn.
b) Định lý.
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
+ Ta có thể viết:
c) Hệ quả.
Trong một đường tròn:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+ Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
5. Góc tạo bởi tiếp tuyến và dây cung
a) Định nghĩa
+ Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.
+ Cung nằm bên trong là cung bị chắn.
b) Định lý.
Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
6. Góc có đỉnh ở bên trong đường tròn
+ Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.
+ Hình vẽ: Góc ∠BEC là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là 
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Hay 
7. Góc có đỉnh ở bên ngoài đường tròn
+ Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.
+ Hai cung bị chắn là hai cung nằm bên trong góc, hình vẽ trên: Góc ∠BEC là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Hay 
8. Tứ giác nội tiếp
a) Định nghĩa
Một tứ giác có bốn đỉnh nằm tên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)
b) Định lý.
+ Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
+ Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.
c) Dấu hiệu nhận biết tứ giác nội tiếp
+ Tứ giác có tổng hai góc đối bằng 180°.
+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
+ Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
+ Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
+ Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hìn chữ nhật, hình vuông, hình thang cân.
9. Đường tròn ngoại tiếp, đường tròn nội tiếp
a) Định nghĩa
+ Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn.
+ Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.
b) Định lý
+ Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
+ Tâm của hai đường tròn này trùng nhau và được gọi là tâm của đa giác đều.
+ Tâm này là giao điểm hai đường trung trực của hai cạnh hoặc là hai đường phân giác của hai góc.
10. Độ dài đường tròn
“ Độ dài đường tròn” hay còn được gọi là “ chu vi đường tròn” được kí hiệu là C.
Ta có: C = 2πR hoặc C = πd
Trong đó: C là độ dài đường tròn.
R là bán kính đường tròn.
d là đường kính của đường tròn
11. Độ dài của cung tròn
Độ dài cung tròn n° là I = πRn/180.
Trong đó: l là độ dài cung tròn n°.
R là bán kính đường tròn.
n là số đo độ của góc ở tâm.
12. Diện tích hình tròn
Công thức diện tích hình tròn là:
Trong đó: S là diện tích của đường tròn.
R là bán kính đường tròn.
d là đường kính của đường tròn
13. Diện tích của hình quạt tròn
Công thức diện tích hình quạt tròn là:
Trong đó: S là diện tích của hình quạt tròn.
R là bán kính đường tròn.
l là độ dài cung tròn n°.
Câu 1: Cho hình vẽ sau:
Tính số đo cung nhỏ AB,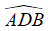 
từ đó so sánh cạnh AC và AD
Lời giải
Ta có:
Câu 2: Cho đường tròn (O; R) đường kính BC cố định. Điểm A di động trên đường tròn khác B và C. Vẽ đường kính AOD. Xác định vị trí điểm A để diện tích ΔABC đạt giá trị lớn nhất, khi đó 
Lời giải
Câu 3: Cho nửa đường tròn đường kính AB = 2m, dây CD // AB (C ∈ AD⌢). Tính độ dài các cạnh của hình thang ABCD biết chu vi hình thang bằng 5cm.
Lời giải
Ta có:
Câu 4: Cho đường tròn (O) và điểm M nằm ngoài đường tròn, từ M vẽ cát tuyến MAB đến đường tròn. C là điểm trên đường tròn khác A và B. Chứng minh rằng MC là tiếp tuyến của đường tròn (O) khi và chỉ khi MC2 = MA.MB .
Lời giải
Câu 5: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D.
Chứng minh AB2 = BD.BC
Lời giải
Câu 6: Cho cung AB cố định tạo bởi các bán kính OA, OB vuông góc với nhau, điểm I chuyển động trên cung AB. Trên tia OI lấy điểm M sao cho OM bằng tổng các khoảng cách từ I đến OA và OB. Tìm quỹ tích các điểm M.
Lời giải
Kết luận: Quỹ tích (tập hợp) điểm M là cung AmB, một phần của cung chứa góc 45° dựng trên OB nằm bên trong góc vuông AOB.
Câu 7: Cho nửa đường tròn (O) đường kính AC. C là một điểm trên nửa đường tròn. Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách từ C đến AB.
Lời giải
Kết luận: Quỹ tích (tập hợp) các điểm D khi C chạy trên nửa đường tròn đường kính AB là đường tròn đường kính OP với P là điểm chính giữa cung AB.
Câu 8: Giả sử A và B là hai điểm phân biệt trên đường tròn (O). Các tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại điểm M. Từ A kẻ đường thẳng song song với MB cắt đường tròn (O) tại C. MC cắt đường tròn (O) tại E. Các tia AE và MB cắt nhau tại K. Chứng minh rằng MK2 = AK.EK và MK = KB.
Lời giải
Câu 9: Cho tam giác cân ABC (AB = AC) . Gọi O là trung điểm của BC. Dựng đường tròn (O) tiếp xúc với các cạnh AB, AC tại D, E. M là điểm chuyển động trên cung nhỏ DE tiếp tuyến với đường tròn (O) tại M cắt AB, AC tại P, Q. Chứng minh BC2 = 4BP.CQ và tìm vị trí điểm M để diện tích tam giác APQ lớn nhất.
Lời giải
Câu 10: Trên đường tròn (O) cho các điểm A, B, C, D theo thứ tự đó. Gọi A1, B1, C1, D1 lần lượt là điểm chính giữa của các cung AB, BC, CD và DA. Chứng minh các đường thẳng A1C1 và B1D1 vuông góc với nhau
Lời giải
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
