Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9: Chương 3 Hình học nâng cao chọn lọc, có đáp án. Tài liệu có 19 trang gồm 37 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Chương 3 Hình học nâng cao đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.
Giới thiệu về tài liệu:
- Số trang: 19 trang
- Số câu hỏi trắc nghiệm: 37 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Chương 3 Hình học nâng cao có đáp án – Toán lớp 9:

Chương 3 Hình học nâng cao
Câu 1: Số đo cung lớn BnC trong hình bên là:
A. 280o
B. 290o
C. 300o
D. 310o
Lời giải:
Ta có tổng số đo cung nhỏ BmC và số đo cung lớn BnC là 360o
Mặt khác số đo cung nhỏ BmC = 80o. Từ đó ra suy ra số đo cung lớn BnC là:
360o – 80o = 280o
Đáp án cần chọn là: A
Câu 2: Cho hình vẽ ở bên. Khi đó mệnh đề đúng là:
Lời giải:
Góc 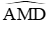
Đáp án cần chọn là: A
Câu 3: Cho hình vẽ (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C). Biết 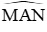
Khi đó 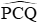
A. 60o
B. 70o
C. 80o
D. 90o
Lời giải:
Ta nhận thấy 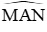
Ta lại có 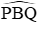
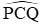
Đáp án cần chọn là: C
Câu 4: Cho hình vẽ bên. Mệnh đề nào sau đây là sai?
Lời giải:
Ta có 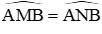
Ta lại có 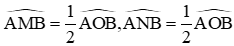
Đáp án cần chọn là: D
Câu 5: Cho đường tròn (O). Trên (O) lấy ba điểm A, B, D sao cho 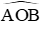
Khi đó ∆ABD là:
A. Tam giác đều
B. Tam giác vuông tại D
C. Tam giác vuông cân tại D
D. Tam giác vuông tại A
Lời giải:
Từ mối liên hệ về số đo góc ở tâm và số đo góc nội tiếp ta có:
∆ABD có AD = BD nên cân tại D, có một góc 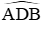
Đáp án cần chọn là: A
Câu 6: Cho tứ giác ABCD nội tiếp đường tròn (O). Biết
A. 50o
B. 130o
C. 15o
D. 65o
Lời giải:
Ta có:
Do đó 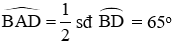
Đáp án cần chọn là: D
Câu 7: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Vẽ cát tuyến CAD vuông góc với AB (C ∈ (O), D ∈ (O’)). Tia CB cắt (O’) tại E, tia DB cắt (O) tại F. Khi đó
Lời giải:
Vậy ba điểm B, O, C thẳng hàng.
Chứng minh tương tự ta nhận được B, O’, D thẳng hàng
Trong (O), các góc 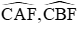
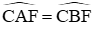
Trong (O’) các góc 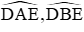
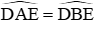
Mặt khác là các góc đối đỉnh, do đó 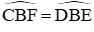
Từ (1), (2), (3) ta suy ra
Đáp án cần chọn là: C
Câu 8: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Khi đó tứ giác ABEC là:
A. Hình bình hành
B. Hình thang
C. Hình thang cân
D. Hình thoi
Lời giải:
Do DE là đường kính của (O; R) nên 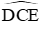
Do đó CD ⊥ CE. Mặt khác theo giả thiết ta có CD ⊥ AB
Do đó AB // CE. Vậy tứ giác ABEC là hình thang (1)
Mặt khác các dây CE, AB là hai dây song song của (O) chắn hai cung AC và BE nên cung AC = cung BE ⇒ AC = BE (2)
Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân
Đáp án cần chọn là: C
Câu 9: Cho hình vẽ dưới đây:
Khi đó mệnh đề đúng là:
Lời giải:
Ta áp dụng công thức về góc có đỉnh ở trong và ở ngoài đường tròn bị chắn bởi cung ta nhận được
Đáp án cần chọn là: B
Câu 10: Qua điểm A nằm ngoài đường tròn (O) kẻ hai cát tuyến ABC và ADE với đường tròn đó (B nằm giữa A và C, D nằm giữa A và E). Kẻ dây BF // DE. Khi đó kết luận đúng là:
A. AC. AE = DC. DF
B. AC. DF = DC. AE
C. AE. CE = DF. CF
D. AC. CE = DC. CF
Lời giải:
Mặt khác ta có 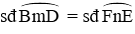
Theo tính chất về góc có đỉnh bên ngoài đường tròn ta có:
Theo tính chất của góc nội tiếp bị chắn bởi cung ta có:
Đáp án cần chọn là: B
Câu 11: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Trên (O) lấy điểm D thuộc cung AC. Gọi E = AC ∩ BD, F = AD ∩ BC. Khi đó mệnh đề đúng là:
Lời giải:
ABC cân tại A nên AB = AC suy ra
Áp dụng kết quả trên và theo tính chất của góc ngoài đường tròn ta có:
Đáp án cần chọn là: D
Câu 12: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi P, Q, R lần lượt là giao điểm của các tia phân giác trong góc A, B, C với đường tròn. Giả sử rằng S = AP ∩ RQ. Khi đó:
Lời giải:
Ta có tia phân giác AP chia đôi cung BC thành hai cung bằng nhau, hay
Khi đó theo tính chất của góc có đỉnh bên trong đường tròn ta có:
Đáp án cần chọn là: D
Câu 13: Cho tam giác nhọn ABC (AB > BC) nội tiếp đường tròn (O). D là điểm chính giữa cung AC. Giả sử {E} = AB ∩ CD, {F} = AD ∩ BC. Khi đó:
Lời giải:
Theo tính chất của góc ngoài đường tròn ta có:
Mặt khác ta có D là điểm chính giữa cung AC nên:
Đáp án cần chọn là: C
Câu 14: Cho hình vẽ, biết số đo cung BmD là 120o. Khi đó:
Lời giải:
Xét tam giác AOB vuông tại B (do AB là tiếp tuyến) nên:
Đáp án cần chọn là: D
*Chú ý: Các em có thể sử dụng tính chất góc có đỉnh nằm ngoài đường tròn để tính
Câu 15: Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với (O) tại A và B. Qua A vẽ đường thẳng song song với MB cắt đường tròn tại C
Nối C với M cắt đường tròn (O) tại D. Nối A với D cắt MB tại E. Chọn câu đúng
A. ME = 2EB
B. 2ME = EB
C. ME = EB
D. 3ME = 2EB
Lời giải:
Xét ∆ABE và ∆BDE có:
+ Ê chung
+ 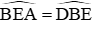
Mà 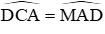
Đáp án cần chọn là: C
Câu 16: Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đoạn AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt tại E và F. Tiếp tuyến tại C với nửa đường tròn cắt EF tại M và cắt AB tại N. Khi đó:
A. ME = MF
B. 2ME = MF
C. ME = 2MF
D. 2ME = 3MF
Lời giải:
Ta có 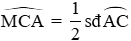
Từ (1) và (2) suy ra 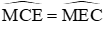
Chứng minh tương tự ta có MC = MF
Suy ra ME = MF
Đáp án cần chọn là: A
Câu 17: Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn sao cho 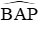
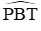
A. 30o
B. 45o
C. 60o
D. 90o
Lời giải:
Xét (O) có góc PAB là góc nội tiếp chắn cung BP, góc PBT là góc tạo bởi tia tiếp tuyến và dây cung BP nên 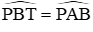
Đáp án cần chọn là: A
Câu 18: Cho hình vẽ ở bên. Biết 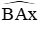
Hãy tính số đo của cung bị chắn AB
A. 100o
B. 60o
C. 80o
D. 40o
Lời giải:
Đáp án cần chọn là: D
Câu 19: Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Gọi M là giao điểm của AO và BC. Khi đó tam giác AMB là:
A. Tam giác vuông có một góc 30o
B. Tam giác vuông có một góc 60o
C. Tam giác vuông có cạnh góc vuông bằng nửa cạnh huyền
D. Các đáp án trên đều đúng
Lời giải:
Xét đường tròn (O) có dây BC = R = OC = OB nên ∆BOC là tam giác đều.
Lại có 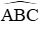
Do góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn nên:
Lại có AB = AC (tính chất hai tiếp tuyến cắt nhau) và OB = OC = R nên AO là đường trung trực của BC. Hay AO ⊥ BC tại M, suy ra
Như vậy tam giác AMB vuông tại M và có
Nên đáp án A, B đều đúng
Hay cạnh góc vuông AM bằng nửa cạnh huyền AB. Vì vậy đáp án C cũng đúng.
Đáp án cần chọn là: D
Câu 20: Cho hình vẽ. Khi đó đáp án đúng là:
Lời giải:
Đáp án cần chọn là: B
Câu 21: Cho ∆ABC nội tiếp đường tròn (O; R) có độ dài các cạnh là AB = c, BC = a; CA = b kẻ AH ⊥ BC, AO cắt (O) tại D. Diện tích S của ∆ABC là:
Lời giải:
Các góc 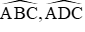
Đáp án cần chọn là: A
Câu 22: Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM. Gọi S1; S2 lần lượt là diện tích của tam giác CAN và tam giác BCM. (hình vẽ)
Chọn câu đúng.
Lời giải:
Xét ∆CAN và ∆BCM có:
+) AC = BC (vì C là điểm chính giữa của cung AB)
+) 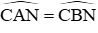
+) Theo giả thiết ta có AN = BM
Do đó ∆ACN và ∆BCM (c.g.c). Hai tam giác bằng nhau nên diện tích bằng nhau. Do đó S1 = S2
Đáp án cần chọn là: C
Vận dụng cao: Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM. Gọi S1; S2 lần lượt là diện tích của tam giác CAN và tam giác BCM. (hình vẽ)
Khi đó tam giác AMN là tam giác:
A. Đều
B. Cân
C. Vuông
D. Vuông cân
Lời giải:
Xét ∆CAN và ∆BCM có:
+) AC = BC (vì C là điểm chính giữa của cung AB)
+) 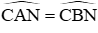
+) Theo giả thiết ta có AN = BM
Do đó ∆ACN và ∆BCM (c.g.c). Do đó CN = CM
Vì vậy ∆CMN là tam giác cân tại C (1)
+) 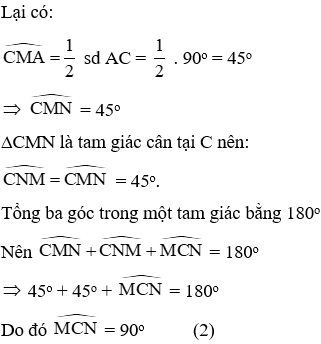
Từ (1) và (2) suy ra CMN vuông cân tại C
Đáp án cần chọn là: D
Câu 23: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Cho biết thêm rằng R = 1. Giá trị lớn nhất của biểu thức Q = MA + MB + MC + MD là:
A. 1
B. 2
C. 3
D. 4
Lời giải:
Do DE là đường kính của (O; R) nên 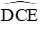
Do đó CD ⊥ CE. Mặt khác, theo giả thiết có CD ⊥ AB. Do đó AB // CE
Mặt khác các dây CE, AB là hai dây song song của (O) chắn hai cung AC và BE nên cung AC bằng cung BE hay cung AE bằng cung BC suy ra EA = BC
Mặt khác 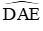
Do đó MA2 + MB2 + MC2 + MD2 = (MA2 + MD2) + (MB2 + MC2) = AD2 + BC2
= DE2 = 4R2 = 4
Áp dụng bất đẳng thức Cô-si cho MA2, MB2 ta có:
MA2 + MB2 ≥ 2MA.MB ⇒ 2(MA2 + MB2) ≥ 2MA2 + 2MB2 ≥ MA2 + MB2 + 2MA.MB = (MA + MB)2
Tương tự
2(MC2 + MD2) ≥ (MC + MD)2
Bằng cách tương tự trên ta chứng minh được:
2[(MA + MB)2 + (MC + MD)2] ≥ (MA + MB + MC + MD)2
Từ đó suy ra:
4(MA2 + MB2 + MC2 + MD2) ≥ (MA + MB + MC + MD)2.
Vì vậy (MA + MB + MC + MD)2 ≤ 4.4 = 42 ⇒ MA + MB + MC + MD ≤ 4
Dấu “=” xảy ra khi và chỉ khi MA = MB = MC = MD. Khi đó M ≡ O
Đáp án cần chọn là: D
Câu 24: Cho hình vẽ dưới đây. Giả sử số đo các cung AnC, CpD, DqB lần lượt có số đo là α, β (2α + β < 360°). Khi đó:
Lời giải:
Theo giả thiết ta có:
Theo tính chất góc có đỉnh nằm bên ngoài của đường tròn và áp dụng (1) ta có:
Ta cũng có 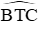
Đáp án cần chọn là: C
Câu 25: Cho tứ giác ABCD nội tiếp đường tròn tâm O bán kính bằng a. Biết rằng AC ⊥ BD. Khi đó để AB + CD đạt giá trị lớn nhất thì:
A. AC = AB
B. AC = BD
C. DB = AB
D. Không có đáp án nào đúng
Lời giải:
Vẽ đường kính CE của đường tròn (O)
Ta có 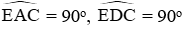
Từ đó ta có AE ⊥ AC. Mặt khác theo giả thiết AC ⊥ BD
Kéo theo AE // BD. Vậy AEDB là hình thang
Do hình thang AEDB nội tiếp (O) nên nó phải là hình thang cân
Kéo theo AB = DE (các cạnh bên hình thang cân)
Từ đó ta có AB2 + CD2 = DE2 + DC2 = EC2 = (2a)2 = 4a2 (do ∆EDC vuông tại D)
Áp dụng bất đẳng thức Cô-si cho cặp số (AB2 + BD2), ta có:
AB2 + BD2 ≥ 2AB. CD ⇒ 2(AB2 + CD2) ≥ AB2 + BD2 + 2. AB. CD
= (AB + CD)2
Kéo theo (AB + CD)2 ≤ 2.(4a2) = 8a2 ⇒ AB + CD ≤ 2a√2
Đẳng thức xảy ra khi và chỉ khi AB = CD
Xét tam giác ∆ABI, ∆DCI có AB = CD, 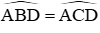
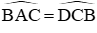
Do đó ∆ABI = ∆DCI (g.c.g)
Kéo theo AI = ID, IB = IC. Suy ra AC = AI + IC = ID + IB = BD
Đáp án cần chọn là: B
Câu 26: Cho tam giác ABC không cân, nội tiếp đường tròn (O), BD là đường phân giác của góc 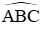
A. AN = NC.
B. AD = DN
C. AN = 2NC
D. 2AN = NƯỚC
Lời giải:
Gọi M là trung điểm của AC. Do E là điểm chính giữa cung AC nên EM ⊥ AC.
Do đó EM đi qua tâm của đường tròn (O). Giả sử rằng G = DF ∩ (O).
Do 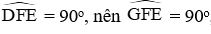
Do 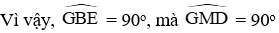
Kéo theo tứ giác BDMG là tứ giác nội tiếp đường tròn đường kính GD
Vì vậy 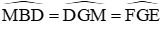
Lại có tứ giác BFEG là tứ giác nội tiếp nên 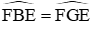
Từ (1) và (2) ta suy ra 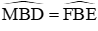
Vì vậy M ≡ N hay N là trung điểm của AC nên AN = NƯỚC
Đáp án cần chọn là: A
Câu 27: Đầu xóm em có đào 1 cái giếng, miệng giếng hình tròn có đường kính 2cm. Xung quanh miệng giếng ngta xây 1 cái thành rộng 0,4 (m). Tính tiện tích thành giếng là:
A. π (m2)
B. 0,44π (m2)
C. 1,76π (m2)
D. 0,96π (m2)
Lời giải:
Quan sát hình vẽ, ta cần tính phần diện tích giới hạn bởi hai đường tròn
Đường kính của giếng là 2 (m) nên bán kính của giếng là 1 (m)
Bán kính đường tròn ngoài là 1 + 0,4 = 1,4 (m). Gọi S1, S2 lần lượt là diện tích của hình tròn nhỏ và lớn.
Khi đó ta có:
S1 = π. 12 = π (m2), S2 = π.(1,4)2 = 1,96π (m2).
Diện tích của thành giếng là S2 – S1 = 1,96π − π = 0,96π (m2)
Đáp án cần chọn là: D
Câu 28: Cho biết diện tích của hình quạt OAB bằng 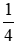
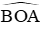
A. 90o
B. 60o
C. 45o
D. 120o
Lời giải:
Đặt α = 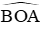
Đáp án cần chọn là: A
Câu 29: Gọi M, N lần lượt là trung điểm của các cạnh AB, CD của hình chữ nhật ABCD. Biết rằng đường tròn ngoại tiếp hình chữ nhật ABCD có đường kính 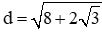
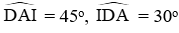
Lời giải:
Do M, N là trung điểm của các cạnh hình chữ nhật nên MN ⊥ AB.
Đáp án cần chọn là: D
Câu 30: Cho đường tròn (O; R) và một điểm M nằm ở ngoài đường tròn sao cho MO = 2R. Đường thẳng d đi qua M, tiếp xúc với đường tròn (O; R) tại A. Giả sử N = MO ∩ (O; R). Kẻ hai đường kính AB, CD khác nhau của (O; R). Các đường thẳng BC, BD cắt đường thẳng d lần lượt tại P, Q. Khi đó:
A. 3BQ – 2AQ > 4R
B. 3BQ – 2AQ < 4R
C. 3BQ – 2AQ = 4R
D. A, B, C đều sai
Lời giải:
Xét ∆QAB vuông ở A ta có AD ⊥ QB. Suy ra QB. DB = AB2 = 4R2 và
QB.QD = AG2
Cộng từng vế của (3) và (4) ta nhận được:
1QB + DB + QD > 4R + 2AQ ⇒ 3QB – 2AQ > 4R
Đáp án cần chọn là: A
Câu 31: Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax và By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt tại C và D. Khi đó độ dài AC + BD nhỏ nhất khi:
A. cung MA = cung MB
B. AM = MB
C. AC = BD = R
D. A, B, C đều đúng
Lời giải:
Do CM, DM là các tiếp tuyến nên ta có MD = BD, CM = CA
Từ đó CA + BD = CM + MD = CD
Từ C hạ đường cao CH xuống BD
Khi đó ∆HCD vuông tại H, có CD là cạnh huyền và CH là cạnh góc vuông nên CD ≥ CH. Mặt khác CH // BA và CA ⊥ CH, BH ⊥ CH nên CHBA là hình chữ nhật.
Do đó CH = BA. Vì vậy CD ≥ AB
Do đó CA + BD nhỏ nhất khi và chỉ khi CA + BD = AB ⇔ CD = AB
⇔ CD = CH ⇔ CD // AB. Khi đó ta có ABDC là hình chữ nhật và do đó AC = BD. Mặt khác O là trung điểm AB nên M là trung điểm CD. Kéo theo CA = CM = MD = BD = R
Đáp án cần chọn là: D
Câu 32: Cho hai đường tròn (O1) và (O2) có bán kính bằng R cắt nhau tại hai điểm A, B. Qua A vẽ cát tuyến cắt hai đường tròn (O1) và (O2) thứ tự tại E và F. 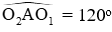
Lời giải:
Gọi S1, S2, S3 lần lượt là diện tích của hình quạt AO2B, AO1B và của tứ giác AO1BO2.
Áp dụng định lý Pytago trong tam giác vuông AHO2 ta nhận được:
Ta có thể kiểm tra được các tam giác ∆AHO2, ∆BHO2, ∆AHO1 là các tam giác bằng nhau. Do đó diện tích của tứ giác AO2BO1 bằng 4 lần diện tích tam giác AHO2.
Đáp án cần chọn là: C
Câu 33: Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Trên Ax lấy điểm M rồi kẻ tiếp tuyến MP cắt By tại N. Khi đó tỉ số 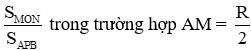
Lời giải:
Theo tính chất hai tiếp tuyến cắt nhau ta có:
Ta lại có 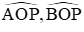
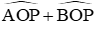
Nên tam giác MON là tam giác vuông tại O có OP ⊥ MN (OP là tiếp tuyến)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông MON ta có:
OP2 = PN. PM
Ta lại có OP = R; AM = PM; BN = N (tính chất hai tiếp tuyến cắt nhau)
Do đó AM. BN = R2 hay PN.PM = R2
Ta có 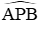
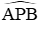
Từ (4); (5) và 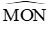
Đáp án cần chọn là: C
Câu 34: Cho tam giác ABC cân tại A, nội tiếp đường tròn (O; R). Gọi D là trung điểm của AC; tia BD cắt tiếp tuyến tại A với đường tròn (O) tại điểm E; EC cắt (O) tại F. Giả sử rằng DF // BC. Khi đó cos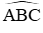
Lời giải:
Giả sử rằng tia FD cắt AB tại M, cắt (O) tại N. Theo giả thiết DF // BC, và AH là trục đối xứng của BC và của đường tròn (O) nên F, D theo thứ tự là điểm đối xứng với N, M qua AH
Xét ∆NDA, ∆CDF có 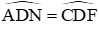
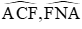
Đáp án cần chọn là: A
Câu 35: Cho A là điểm cố định trên đường tròn (O; R). Gọi A và AC là hai dây cung thay đổi trên đường tròn (O) thỏa mãn 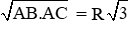
A. ∆ABC cân
B. ∆ABC đều
C. ∆ABC vuông cân
D. ∆ABC vuông
Lời giải:
Kẻ AH ⊥ BC, OI ⊥ BC, đường kính AD
Ta chứng minh được ∆AHC ~ ∆ABD (g – g)
Do AH = 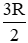
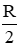
Đáp án cần chọn là: B
* Chú ý: Học sinh thường làm sai như sau:
Diện tích tam giác ABC lớn nhất khi BC = 2R, AH = R mà không chú ý đến điều kiện
Câu 36: Cho đường tròn (O; R), đường kính AB cố định, đường kính CD thay đổi (CD ≠ AB). Các tia BC, BD cắt tiếp tuyến của đường tròn (O) tại A lần lượt tại E, F. Khi CD thay đổi. Giá trị nhỏ nhất của EF theo R là:
A. 4R
B. 2R
C. 6R
D. R
Lời giải:
Vậy giá trị nhỏ nhất của EF là 4R đạt được khi CD ⊥ AB
Đáp án cần chọn là: A
Câu 37: Cho tam giác đều ABC có cạnh bằng 1, nội tiếp trong đường tròn tâm O. Đường cao AD của tam giác ABC cắt đường tròn tại điểm H. Diện tích phần giới hạn bởi cung nhỏ BC và hình BOCH là:
Lời giải:
Ta có: AD là đường cao của ABC đều nên nó cũng là trung tuyến ⇒ BD = DC)
Tứ giác OBHC có 4 cạnh bằng nhau nên là hình thoi
Đáp án cần chọn là: C