Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài tập ôn chương 3: Góc với đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài tập ôn chương 3: Góc với đường tròn
Chứng minh rằng
Chứng minh rằng
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu hai tam giác đồng dạng ta suy ra các cạnh tương ứng tỉ lệ.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải:
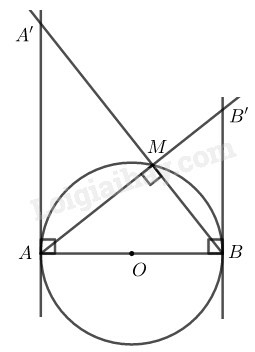
Xét và
(vì cùng phụ với )
Suy ra: đồng dạng
(góc nội tiếp chắn nửa đường tròn)
vuông tại Theo hệ thức lượng trong tam giác vuông ta có:
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu là một điểm trên cung thì:
+) Số đo của nửa đường tròn bằng
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải:
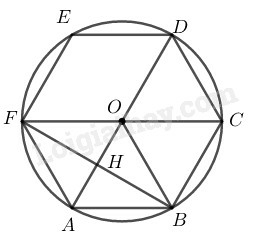
Lục giác đều nội tiếp trong đường tròn
Nên là đường kính của đường tròn
Ta có:
Nên tứ giác là hình thoi
Gọi giao điểm của và là
Ta có: (tính chất hình thoi)
Suy ra:
Phương pháp giải:
* Phân tích:
+) Giả sử đã có một hình thỏa mãn điều kiện bài toán
+) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)
+) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)
* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
Lời giải:
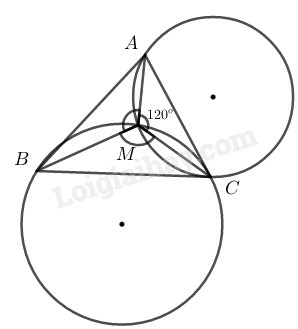
Phân tích:
Giả sử là điểm nằm trong sao cho
Vì
Nên
Khi đó, điểm nhìn các cạnh của dưới góc bằng
Cách dựng:
- Dựng cung chứa góc vẽ trên đoạn
- Dựng cung chứa góc vẽ trên đoạn
- Giao điểm thứ hai ngoài của hai cung này là điểm phải dựng.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với cotang góc kề.
+) Trong đường tròn độ dài của một cung được tính theo công thức:
Lời giải:
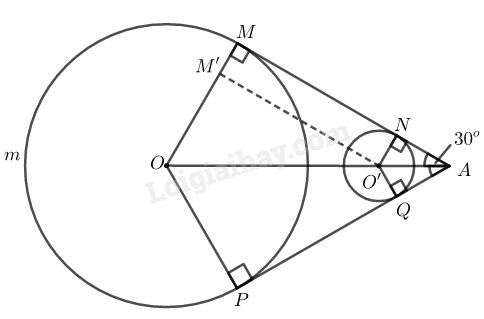
+) Vì hai tiếp tuyến chung của đường tròn và cắt nhau tại nên thẳng hàng.
(tính chất hai tiếp tuyến cắt nhau)
+) Trong tam giác vuông có
+) Trong tam giác vuông có
Từ đó:
+) Trong tứ giác có ;
Suy ra: (tổng bốn góc trong tứ giác bằng
Độ dài cung nhỏ là:
+) Trong tứ giác có ;
Suy ra: (tổng bốn góc trong tứ giác bằng nên số đo cung nhỏ bằng
Độ dài cung lớn là
Chiều dài của dây cua – roa mắc qua hai ròng rọc là:
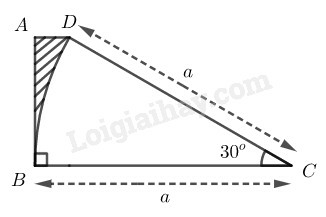
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng cạnh huyền nhân với góc đối hoặc góc kề.
+) Diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao.
+) Diện tích hình quạt tròn bán kính cung được tính theo công thức:
Lời giải:
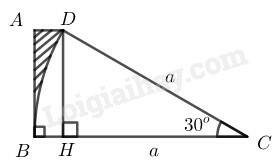
Diện tích phần gạch sọc là hiệu giữa diện tích hình thang và diện tích hình quạt tròn có góc ở tâm của đường tròn bán kính bằng a.
Từ kẻ , suy ra là hình chữ nhật.
Trong tam giác vuông có
(do là hình chữ nhật)
Diện tích của hình thang bằng:
Diện tích hình quạt tròn bằng:
Diện tích phần gạch sọc:
Chứng minh đường tròn tiếp xúc với cạnh
Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Tính chất tia phân giác của một góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với góc đối.
+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh huyền nhân với góc kề.
+) Diện tích của một hình tròn bán kính được tính theo công thức: .
Lời giải:
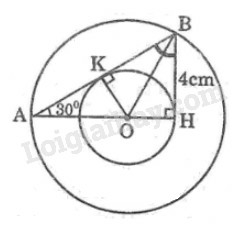
Kẻ tại
Vì là đường phân giác của (gt)
(tính chất đường phân giác)
Suy ra: cũng là bán kính của đường tròn
Vậy đường tròn tiếp xúc với tại
có ;
Suy ra:
Suy ra: cân tại nên
Vậy
có ;
Diện tích đường tròn nhỏ:
Diện tích đường tròn lớn:
Diện tích hình vành khăn:
Tìm quỹ tích điểm
Tính diện tích phần chung của hai nửa hình tròn đường kính và
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Hình thoi có một góc vuông là hình vuông.
+) Diện tích hình quạt tròn bán kính cung được tính theo công thức:
+) Trong đường tròn độ dài của một cung được tính theo công thức:
Lời giải:
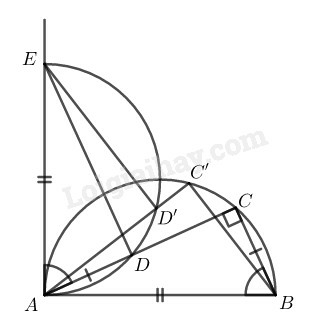
Chứng minh thuận
Nối Xét và
(hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra:
Mà (góc nội tiếp chắn nửa đường tròn)
Điểm chuyển động trên nửa đường tròn đường kính thì điểm luôn nhìn đoạn cố định dưới một góc bằng nên điểm nằm trên nửa đường tròn đường kính nằm trong nửa mặt phẳng bờ chứa nửa đường tròn đường kính
Chứng minh đảo:
Trên nửa đường tròn đường kính lấy điểm bất kỳ, đường thẳng cắt nửa đường tròn đường kính tại Nối
Xét và
(các góc nội tiếp chắn nửa đường tròn)
( góc cùng phụ )
Suy ra: (cạnh huyền, góc nhọn)
Vậy khi điểm chạy trên nửa đường tròn đường kính thì quỹ tích điểm là nửa đường tròn đường kính
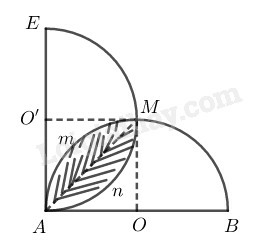
Gọi tâm hai nửa đường tròn đường kính và lần lượt là và giao điểm thứ hai của hai đường tròn là
Ta có: (vì )
Suy ra tứ giác là hình thoi.
Ta lại có: nên tứ giác là hình vuông
Vậy tứ giác là hình vuông
Diện tích phần chung của hai nửa hình tròn bằng diện tích hai quạt tròn có cung trừ đi diện tích hình vuông
Diện tích hình quạt tròn bằng:
Diện tích của hình vuông bằng:
Diện tích phần chung bằng:
(đơn vị diện tích)
Bài tập bổ sung (trang 114,115,116 SBT Toán 9)
là tam giác đều.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải:
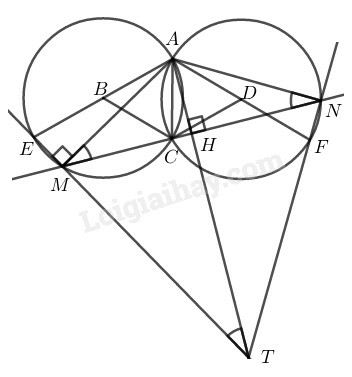
Trong đường tròn ta có:
(hệ quả góc nội tiếp) mà (vì đều)
(góc nội tiếp chắn nửa đường tròn )
Trong đường tròn ta có:
(Hệ quả góc nội tiếp) mà (vì đều)
(góc nội tiếp chắn nửa đường tròn )
hay
Vậy đều.
(theo câu a)
cân tại nên nằm trên đường trung trực
Vì đều nên nằm trên đường trung trực
Suy ra là đường trung trực của nên
có
Vì đều có nên cũng là đường phân giác của nên
có
Từ và suy ra:
Vậy
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong một đường tròn, đường kính đi trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Các đỉnh của một đa giác cùng nhìn một cạnh dưới một góc vuông thì đa giác đó nội tiếp.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải:
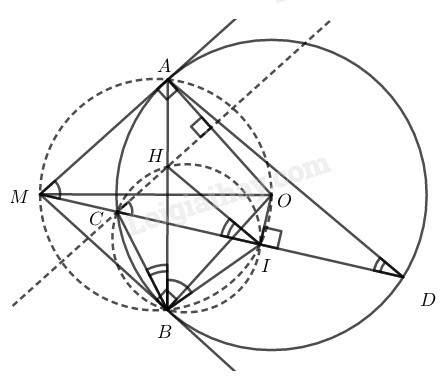
Xét đường tròn có (tính chất tiếp tuyến)
(tính chất tiếp tuyến)
Lại có I là trung điểm dây CD (gt) nên
(đường kính đi qua điểm chính giữa của dây không đi qua tâm thì vuông góc với dây đó)
Từ đó: nhìn cố định dưới một góc bằng nên nằm trên đường tròn bán kính
(Hai góc nội tiếp cùng chắn cung nhỏ )
Lại có mà (chứng minh trên)
Suy ra:
Do đó: (hai góc đồng vị)
Suy ra: hay
Do đó và cùng nằm trên một nửa mặt phẳng bờ chứa đường tạo với một góc bằng nhau nên tứ giác nội tiếp.
(hai góc nội tiếp cùng chắn cung nhỏ ) hay
Trong đường tròn ta có:
( góc nội tiếp cùng chắn cung nhỏ
Từ và suy ra: nên (vì có cặp góc ở vị trí đồng vị bằng nhau)
(Trường hợp cát tuyến đi qua tâm thì ngũ giác suy biến thành tứ giác chứng minh tương tự ta có ).
có đỉnh nằm trên đường tròn.
có hai cạnh là hai dây của đường tròn.
có hai đỉnh là tâm đường tròn và có hai cạnh là hai bán kính.
có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.
Phương pháp giải:
Sử dụng định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải:
Chọn Góc nội tiếp là góc có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.
đi qua các đỉnh của một tam giác.
tiếp xúc với các đường thẳng chứa các cạnh của một tam giác.
tiếp xúc với các cạnh của một tam giác.
nằm trong một tam giác.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
Lời giải:
Chọn Một đường tròn là đường tròn nội tiếp nếu nó tiếp xúc với các cạnh của một tam giác.
có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
có góc bằng nhau.
có cạnh bằng nhau.
có các cạnh tiếp xúc với đường tròn.
Phương pháp giải:
Ta sử dụng kiếnt thức: Tứ giác có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau thì tứ giác đó nội tiếp.
Lời giải:
Chọn Một tứ giác là tứ giác nội tiếp nếu có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
một đường tròn đi qua hai điểm
một đường thẳng song song với
một cung chứa góc dựng trên hai điểm
hai cung chứa góc (đối xứng nhau) dựng trên hai điểm
Phương pháp giải:
Ta sử dụng kiến thức:
+) Với đoạn thẳng và góc cho trước thì quỹ tích các điểm thỏa mãn là hai cung chứa góc dựng trên đoạn
+) Hai cung chứa góc là hai cung tròn đối xứng với nhau qua
Lời giải:
Chọn Quỹ tích các điểm nhìn đoạn thẳng dưới một góc là hai cung chứa góc (đối xứng nhau) dựng trên hai điểm
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài của một đường tròn có đường kính là
Lời giải:
Độ dài đường tròn đường kính là:
Suy ra độ dài nửa đường tròn đường kính là
Vây chọn
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích của một hình tròn bán kính được tính theo công thức:
Lời giải:
Bán kính hình tròn có đường kính là
Diện tích của một hình tròn bán kính là:
Suy ra diện tích của nửa hình tròn có đường kính là:
Vậy chọn
Không tính được.
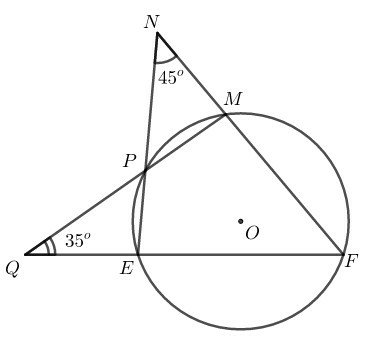
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu là một điểm trên cung thì:
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
Xé đường tròn ta có: (góc nội tiếp)
Ta có:
+) (góc có đỉnh bên ngoài đường tròn)
+) (góc có đỉnh bên ngoài đường tròn)
Mà
Do đó:
Vậy chọn
Không tính được.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
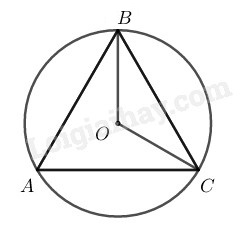
Xét đường tròn ta có: (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Nên
Vậy chọn
Không tính được.
Phương pháp giải:
Ta sử dụng kiến thức: Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
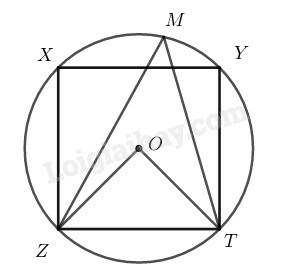
Vì là hình vuông nên , suy ra
Xét đường tròn ta có: (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Vậy chọn