Với giải Bài 95 trang 105 Toán lớp 9 chi tiết trong Ôn tập chương 3 Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài Ôn tập chương 3 Hình học

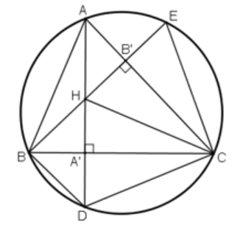
Bài 95 trang 105 SGK Toán lớp 9 Tập 2: Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác ${90}^0$) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng:

a) CD = CE ;    

b) Tam giác BHD cân ;    

c) CD = CH.

Lời giải:

a)

AD vuông góc với BC tại A’ nên $\widehat{AA\text{'}B}={90}^o$

Vì $\widehat{AA\text{'}B}$ là góc có đỉnh ở trong đường tròn chắn hai cung AB và DC nên ta có: 

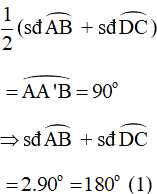
Mặt khác, BE vuông góc với AC tại B’ nên $\widehat{AB\text{'}B}={90}^o$

Vì $\widehat{AB\text{'}B}$ là góc có đỉnh ở trong đường tròn chắn hai cung AB và CE nên ta có:

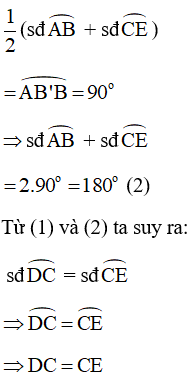
b)

Góc EBC là góc nội tiếp chắn cung BC

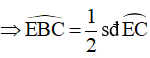
Góc CBD là góc nội tiếp chắn cung DC

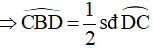
Mà:

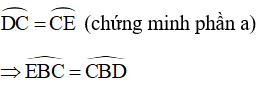
Xét tam giác BHD có:

BA’ vuông góc với HD tại A’  nên BA’ là đường cao

Mà: $\widehat{EBC}=\widehat{CBD}$ (chứng minh trên) nên BA’ cũng là đường phân giác

Do đó, tam giác BHD cân tại B.

c)

Tam giác BHD cân tại B nên BA’ vừa là đường cao vừa là đường trung tuyến và cũng là đường trung trực của đoạn thẳng HD

Điểm C nằm trên đường thẳng BA’

$\Rightarrow CH=CD$