Với giải Hoạt động 1 trang 44 Toán lớp 10 Cánh diều chi tiết trong Bài 3: Dấu của tam thức bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 3: Dấu của tam thức bậc hai.
Hoạt động 1 trang 44 Toán lớp 10: a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai
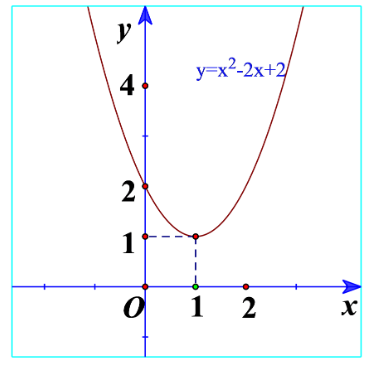
b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai
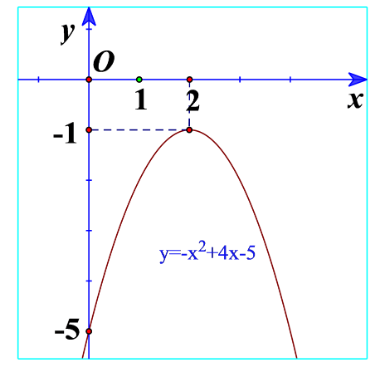
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai với dấu của hệ số a trong trường hợp .
Phương pháp giải:
a) ứng với phần parabol nằm phía trên trục hoành.
b) ứng với phần parabol nằm phía dưới trục hoành.
c) Rút ra nhận xét.
Lời giải:
a) Ta thấy đồ thị nằm trên trục hoành nên .
b) Ta thấy đồ thị nằm dưới trục hoành nên .
c) Ta thấy có hệ số a=1>0 và
có hệ số a=-1
Như thế, khi thì tam thức bậc hai cùng dấu với hệ số a.
Lý thuyết Dấu của tam thức bậc hai
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0), ∆ = b2 – 4ac.
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ \
+ Nếu ∆ > 0 thì f(x) có hai nghiệm x1, x2 (x1 < x2). Khi đó:
– f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng (–∞; x1); (x2; +∞)
– f(x) trái dấu với hệ số a với mọi x thuộc khoảng (x1; x2).
Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:
Câu hỏi khởi động trang 44 Toán lớp 10: Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệm tính toán lợi nhuận y (đồng) theo công thức sau:...
Hoạt động 2 trang 45 Toán lớp 10: a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai....
Hoạt động 3 trang 45 Toán lớp 10: a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai...
Luyện tập vận dụng 1 trang 46 Toán lớp 10: Xét dấu của mỗi tam thức bậc hai sau:...
Luyện tập vận dụng 2 trang 46 Toán lớp 10: Lập bảng xét dấu của tam thức bậc hai:...
Bài 1 trang 48 Toán lớp 10: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?...
Bài 3 trang 48 Toán lớp 10: Xét dấu của mỗi tam thức bậc hai sau:...
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Bài 3: Dấu của tam thức bậc hai
Bài 4: Bất phương trình bậc hai một ẩn
Bài 5: Hai dạng phương trình quy về phương trình bậc hai