Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp

hoa Ngày: 11-10-2022 Lớp 8

4 K

Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp, chi tiết nhất giúp học sinh dễ dàng làm bài tập Chia đa thức một biến đã sắp xếp lớp 8.

Giải bài tập Toán lớp 8 Bài 12: Chia đa thức một biến đã sắp xếp

Trả lời câu hỏi giữa bài

Trả lời câu hỏi trang 30 sgk Toán 8 Tập 1: Kiểm tra lại tích $(x^{2} - 4 x - 3) (2 x^{2} - 5 x + 1)$ có bằng $(2 x^{4} - 13 x^{3} + 15 x^{2} + 11 x - 3)$ hay không.

Phương pháp giải: Áp dụng quy tắc nhân đa thức với đa thức.

Lời giải:

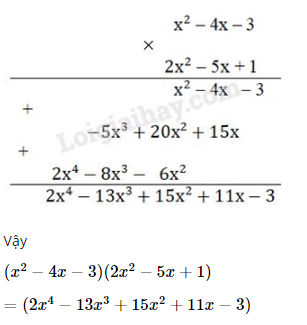
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 1)

Câu hỏi và bài tập (trang 31, 32 sgk Toán 8 Tập 1)

Bài 67 trang 31 sgk Toán 8 Tập 1: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:

a) $(x^{3} - 7 x + 3 - x^{2}) : (x - 3)$ ;

b) $(2 x^{4} - 3 x^{3} - 3 x^{2} - 2 + 6 x) : (x^{2} - 2)$ .

Phương pháp giải: - Sắp xếp đa thức theo lũy thừa giảm dần của biến.

- Áp dụng qui tắc chia hai đa thức một biến đã sắp xếp.

Lời giải:

a) $(x^{3} - 7 x + 3 - x^{2}) : (x - 3)$ ;

Ta có: $x^{3} - 7 x + 3 - x^{2}$ $= x^{3} - x^{2} - 7 x + 3$

Thực hiện phép chia:

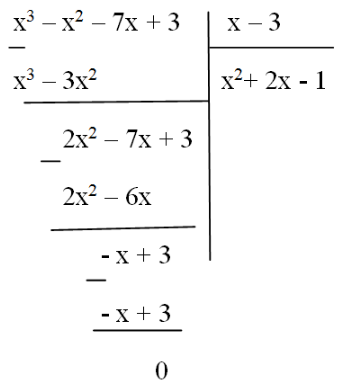
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 3)

Vậy: $(x^{3} - 7 x + 3 - x^{2}) : (x - 3)$ $= x^{2} + 2 x - 1$ .

b) $(2 x^{4} - 3 x^{3} - 3 x^{2} - 2 + 6 x) : (x^{2} - 2)$ .

Ta có: $2 x^{4} - 3 x^{3} - 3 x^{2} - 2 + 6 x$ $= 2 x^{4} - 3 x^{3} - 3 x^{2} + 6 x - 2$

Thực hiện phép chia:

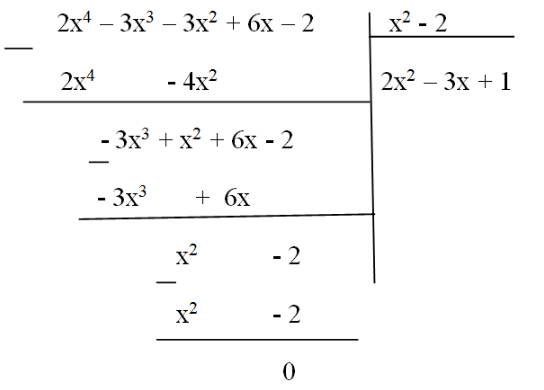
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 2)

Vậy $(2 x^{4} - 3 x^{3} - 3 x^{2} - 2 + 6 x) : (x^{2} - 2)$ $= 2 x^{3} - 3 x + 1$

Bài 68 trang 31 sgk Toán 8 Tập 1: Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:

a) $(x^{2} + 2 x y + y^{2}) : (x + y)$ ;

Phương pháp giải: - Áp dụng hằng đẳng thức đáng nhớ phân tích đa thức bị chia thành nhân tử, sau đó thực hiện phép chia.

- Áp dụng hằng đẳng thức: ${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

$(x^{2} + 2 x y + y^{2}) : (x + y)$

$= {(x + y)}^{2} : (x + y)$

$= x + y$ .

b) $(125 x^{3} + 1) : (5 x + 1)$ ;

Phương pháp giải: - Áp dụng hằng đẳng thức đáng nhớ phân tích đa thức bị chia thành nhân tử, sau đó thực hiện phép chia.

- Áp dụng hằng đẳng thức: $A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$

Lời giải:

$(125 x^{3} + 1) : (5 x + 1)$

$= [{(5 x)}^{3} + 1^{3}] : (5 x + 1)$

$= (5 x + 1) [(5 x)^{2} - 5 x .1 + 1^{2}] : (5 x + 1)$

$= (5 x + 1) (25 x^{2} - 5 x + 1) : (5 x + 1)$

$= 25 x^{2} - 5 x + 1$

c) $(x^{2} - 2 x y + y^{2}) : (y - x)$ .

Phương pháp giải: - Áp dụng hằng đẳng thức đáng nhớ phân tích đa thức bị chia thành nhân tử, sau đó thực hiện phép chia.

- Áp dụng hằng đẳng thức: ${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Lời giải:

$(x^{2} - 2 x y + y^{2}) : (y - x)$

$= {(x - y)}^{2} : [- (x - y)]$

$= - (x - y) = y - x$

Hoặc ta làm như sau:

$\begin{array}{l} (x^{2} - 2 x y + y^{2}) : (y - x) \\ = (y^{2} - 2 x y + x^{2}) : (y - x) \\ = {(y - x)}^{2} : (y - x) \\ = y - x \end{array}$

Bài 69 trang 31 sgk Toán 8 Tập 1: Cho hai đa thức $A = 3 x^{4} + x^{3} + 6 x - 5$ và $B = x^{2} + 1$ . Tìm dư $R$ trong phép chia $A$ cho $B$ rồi viết $A$ dưới dạng $A = B . Q + R$ .

Phương pháp giải: Áp dụng qui tắc chia hai đa thức một biến đã sắp xếp.

Lời giải: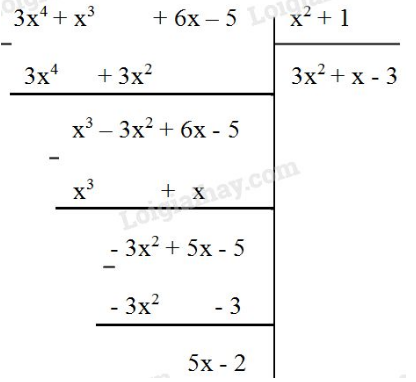
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 4)

Vậy $3 x^{4} + x^{3} + 6 x - 5$ $= (x^{2} + 1) (3 x^{2} + x - 3) + 5 x - 2$

Bài 70 trang 32 sgk Toán 8 Tập 1: Làm tính chia:

a) $(25 x^{5} - 5 x^{4} + 10 x^{2}) : 5 x^{2}$ ;

b) $(15 x^{3} y^{2} - 6 x^{2} y - 3 x^{2} y^{2}) : 6 x^{2} y$ .

Phương pháp giải: Muốn chia đa thức $A$ cho đơn thức $B$ (trường hợp các hạng tử của đa thức $A$ đều chia hết cho đơn thức $B$ ), ta chia mỗi hạng tử của $A$ cho $B$ rồi cộng các kết quả với nhau.

Lời giải:

a) $(25 x^{5} - 5 x^{4} + 10 x^{2}) : 5 x^{2}$

$= (25 x^{5} : 5 x^{2}) + (- 5 x^{4} : 5 x^{2})$ $+ (10 x^{2} : 5 x^{2})$

$= 5 x^{3} - x^{2} + 2$

b) $(15 x^{3} y^{2} - 6 x^{2} y - 3 x^{2} y^{2}) : 6 x^{2} y$

$= (15 x^{3} y^{2} : 6 x^{2} y) + (- 6 x^{2} y : 6 x^{2} y)$ $+ (- 3 x^{2} y^{2} : 6 x^{2} y)$

$= \frac{15}{6} x y - 1 - \frac{3}{6} y = \frac{5}{2} x y - \frac{1}{2} y - 1$ .

Bài 71 trang 32 sgk Toán 8 Tập 1: Không thực hiện phép chia, hãy xét xem đa thức $A$ có chia hết cho đa thức $B$ hay không.

a) $A = 15 x^{4} - 8 x^{3} + x^{2}$

$B = \frac{1}{2} x^{2}$

b) $A = x^{2} - 2 x + 1$

$B = 1 - x$

Phương pháp giải: Đa thức $A$ chia hết cho đa thức $B$ khi và chỉ khi từng hạng tử của $A$ chia hết cho $B$ .

Lời giải:

a) $A = 15 x^{4} - 8 x^{3} + x^{2}$

$B = \frac{1}{2} x^{2}$

Ta có: $A, B$ là các đa thức một biến.

Thực hiện $A$ chia $B$ thì ta lấy từng hạng tử của đa thức $A$ chia cho đa thức $B$ .

$15 x^{4}$ chia hết cho $\frac{1}{2} x^{2}$

$- 8 x^{3}$ chia hết cho $\frac{1}{2} x^{2}$

$x^{2}$ chia hết cho $\frac{1}{2} x^{2}$

Do đó $A$ chia hết cho $B$

b) $A = x^{2} - 2 x + 1$

$B = 1 - x$

$A = x^{2} - 2 x + 1 = (1 - x)^{2}$

Do đó $A$ chia hết cho $B$ .

Bài 72 trang 32 sgk Toán 8 Tập 1: Làm tính chia: $(2 x^{4} + x^{3} - 3 x^{2} + 5 x - 2)$ $: (x^{2} - x + 1)$

Phương pháp giải: Áp dụng qui tắc chia hai đa thức một biến đã sắp xếp.
Lời giải:

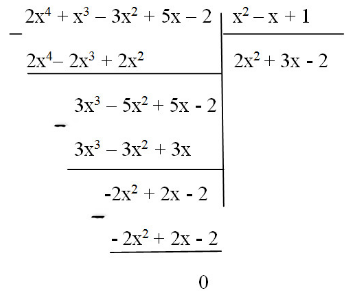
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 5)

Vậy $(2 x^{4} + x^{3} - 3 x^{2} + 5 x - 2) : (x^{2} - x + 1)$ $= 2 x^{2} + 3 x - 2$

Bài 73 trang 32 sgk Toán 8 Tập 1: Tính nhanh:

a) $(4 x^{2} - 9 y^{2}) : (2 x - 3 y)$ ;

b) $(27 x^{3} - 1) : (3 x - 1)$ ;

c) $(8 x^{3} + 1) : (4 x^{2} - 2 x + 1)$ ;

d) $(x^{2} - 3 x + x y - 3 y) : (x + y)$

Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ để phân tích đa thức bị chia thành nhân tử, sau đó thực hiện phép chia.

Lời giải:

a) $(4 x^{2} - 9 y^{2}) : (2 x - 3 y)$

$= [{(2 x)}^{2} - {(3 y)}^{2}] : (2 x - 3 y)$

$= (2 x - 3 y) . (2 x + 3 y) : (2 x - 3 y)$

$= 2 x + 3 y$ ;

b) $(27 x^{3} - 1) : (3 x - 1)$

$= [{(3 x)}^{3} - 1^{3}] : (3 x - 1)$

$= (3 x - 1) . [{(3 x)}^{2} + 3 x .1 + 1^{2}] : (3 x - 1)$

$= (3 x - 1) . (9 x^{2} + 3 x + 1) : (3 x - 1)$

$= 9 x^{2} + 3 x + 1$

c) $(8 x^{3} + 1) : (4 x^{2} - 2 x + 1)$

$= [{(2 x)}^{3} + 1^{3}] : (4 x^{2} - 2 x + 1)$

$= (2 x + 1) [{(2 x)}^{2} - 2 x .1 + 1^{2}] : (4 x^{2} - 2 x + 1)$

$= (2 x + 1) (4 x^{2} - 2 x + 1) : (4 x^{2} - 2 x + 1)$

$= 2 x + 1$

d) $(x^{2} - 3 x + x y - 3 y) : (x + y)$

$\begin{aligned} = [(x^{2} + x y) - (3 x + 3 y)] : (x + y) \\ = [x (x + y) - 3 (x + y)] : (x + y) \\ = (x + y) (x - 3) : (x + y) \\ = x - 3 \end{aligned}$

Bài 74 trang 32 sgk Toán 8 Tập 1: Tìm số $a$ để đa thức $2 x^{3} - 3 x^{2} + x + a$ chia hết cho đa thức $x + 2$ .

Phương pháp giải: Áp dụng định lí: Một phép chia là phép chia hết thì số dư của phép chia phải bằng $0$ .
Lời giải:

Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 6)

Ta có: $2 x^{3} - 3 x^{2} + x + a$ $= (2 x^{2} - 7 x + 15) . (x + 2) + a - 30$

Dư trong phép chia là $(a - 30)$ nên để phép chia là phép chia hết thì dư của phép chia phải bằng $0$ tức là:

$a - 30 = 0 \Rightarrow a = 30$

Vậy $a = 30$ .

Cách khác:

Phân tích $2 x^{3} - 3 x^{2} + x + a$ thành nhân tử có chứa $x + 2.$

Ta có:

$\begin{array}{l} 2 x^{3} - 3 x^{2} + x + a \\ = 2 x^{3} + 4 x^{2} - 7 x^{2} - 14 x + 15 x + 30 - 30 + a \\ = 2 x^{2} (x + 2) - 7 x (x + 2) + 15 (x + 2) + a - 30 \\ = (2 x^{2} - 7 x + 15) (x + 2) + a - 30 \end{array}$

Vì $(2 x^{2} - 7 x + 15) . (x + 2)$ chia hết cho $(x + 2)$ nên để $2 x^{3} - 3 x^{2} + x + a = (2 x^{2} - 7 x + 15) . (x + 2) + a - 30$ chia hết cho $(x + 2)$ thì $a - 30 = 0 \Rightarrow a = 30$

Lý thuyết Chia đa thức một biến đã sắp xếp

1. Các kiến thức cần nhớ: Chia đa thức một biến đã sắp xếp

- Muốn chia đa thức một biến $A$ cho đa thức một biến $B \neq 0$ , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên.

- Với hai đa thức tùy ý $A$ và $B$ của một biến $(B \neq 0)$ , tồn tại duy nhất hai đa thức $Q$ và $R$ sao cho $A = B . Q + R$

Trong đó $R = 0$ hoặc bậc của $R$ thấp hơn bậc của $B .$

+ Nếu $R = 0$ thì phép chia $A$ cho $B$ là phép chia hết.

+ Nếu $R \neq 0$ thì phép chia $A$ cho $B$ là phép chia có dư.

Ví dụ 1:

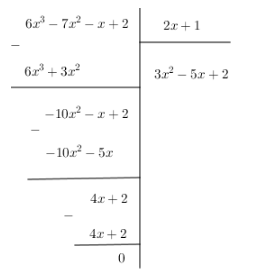
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 7)

Ta viết lại $(6 x^{3} - 7 x^{2} - x + 2) : (2 x + 1) = 3 x^{2} - 5 x + 2$ . Nhận thấy số dư $R = 0$ nên đây là phép chia hết.
Ví dụ 2:

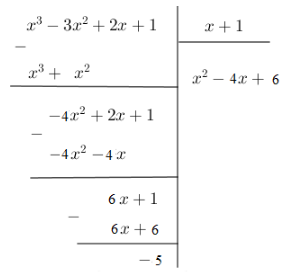
Giải Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp (ảnh 8)

Ta viết lại $x^{3} - 3 x^{2} + 2 x + 1 = (x + 1) (x^{2} - 4 x + 6) - 5$ . Vì $R = - 5 \neq 0$ nên đây là phép chia có dư.

2. Các dạng toán thường gặp:

Dạng 1: Tìm thương, số dư của phép chia đa thức một biến đã sắp xếp

Phương pháp: Muốn chia đa thức một biến $A$ cho đa thức một biến $B \neq 0$ , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên.

Dạng 2: Xác định hằng số $a, b$ sao cho phép chia cho trước là phép chia hết.

Phương pháp: Sử dụng tính chất phép chia hết có số dư $R = 0$ để tìm $a, b$ .

Chú ý:

$A x + B = 0$ với $\forall x \Leftrightarrow {\begin{cases} A = 0 \\ B = 0 \end{cases}$