HĐ3 trang 13 Toán 10 Tập 1 | Kết nối tri thức Giải Toán lớp 10

Thảo Ngày: 23-08-2024 Lớp 10

1.8 K

Với giải HĐ3 trang 13 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 2: Tập hợp và các phép toán trên tập hợp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 2: Tập hợp và các phép toán trên tập hợp

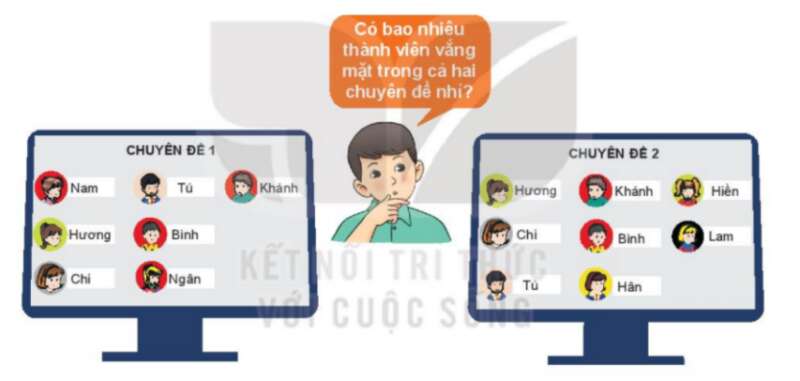
HĐ3 trang 13 Toán lớp 10: Gọi H là tập hợp các bạn tham gia Chuyên đề 2 trong tình huống mở đầu có tên bắt đầu bằng chữ chữ H. Các phần tử của tập hợp H có là phần tử của tập hợp B trong HĐ1 không?

Luyện tập 1 trang 13 Toán lớp 10 Tập 1 | Kết nối tri thức (ảnh 1)

Lời giải:

Ta có: $B =$ {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}

và H = {Hương; Hiền; Hân}

Vậy các phần tử của H đều là phần tử của tập hợp B.

Lý thuyết Các khái niệm cơ bản về tập hợp

1.1. Tập hợp

• Có thể mô tả một tập hợp bằng một trong hai cách sau:

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

a ∈ S: phần tử a thuộc tập hợp S.
a ∉ S: phần tử a không thuộc tập hợp S.

Chú ý: Số phần tử của tập hợp S được kí hiệu là n(S).

Ví dụ:

- Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2, lớn hơn 5 và nhỏ hơn 15.

+ Ta mô tả tập hợp A bằng hai cách như sau:

Cách 1: Liệt kê các phần tử của tập hợp: A = {6; 8; 10; 12; 14};

Cách 2: Chỉ ra tính chất đặc trưng của các phẩn tử: A = { | n ⁝ 2, 5 < n < 15}.

+ Tập hợp A có 5 phần tử, ta viết: n(A) = 5.

+ 10 thuộc tập hợp A, ta viết 10 ∈ A.

+ 15 không thuộc tập hợp A, ta viết 15 ∉ A.

• Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là .

Ví dụ:

+ Tập hợp các nghiệm của phương trình x² + 1 = 0 là tập rỗng;

+ Tập hợp những người sống trên Mặt Trời là tập rỗng.

1.2. Tập hợp con

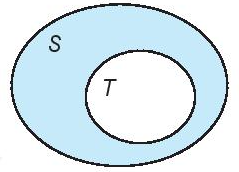
• Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và viết là T ⊂ S (đọc là T chứa trong S hoặc T là tập con của S).

- Thay cho T ⊂ S, ta còn viết S ⊃ T (đọc là S chứa T).

- Kí hiệu T ⊄ S để chỉ T không là tập con của S.

Nhận xét:

- Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng:

∀ x, x ∈ T ⇒ x ∈ S.

- Quy ước tập rỗng là tập con của mọi tập hợp.

• Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.

Tài liệu VietJack