Với giải Bài 31 trang 59 Toán lớp 9 chi tiết trong Bài 5: Hệ số góc của đường thẳng y = ax + b (a # 0) giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 5: Hệ số góc của đường thẳng y = ax + b ( a # 0)
a) Vẽ đồ thị của hàm số :
b) Gọi lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.
Chứng minh rằng
Tính số đo các góc
Phương pháp giải:
a) Cách vẽ đồ thị hàm số : Đồ thị hàm số là đường thẳng:
+) Cắt trục hoành tại điểm
+) Cắt trục tung tại điểm
Xác định tọa độ hai điểm và sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số
b) Góc tạo bởi đường thẳng là góc ta có:
+) Với , góc là góc tù.
+) Với , góc là góc nhọn.
Hoặc sử dụng công thức lượng giác trong tam giác vuông:
vuông tại khi đó:
a)
+ Hàm số
Cho
Cho
Đồ thị hàm số là đường thẳng đi qua hai điểm và
+ Hàm số
Cho
Cho
Đồ thị hàm là đường thẳng đi qua hai điểm và
+ Hàm số
Cho
Cho
Đồ thị hàm số là đường thẳng đi qua hai điểm và
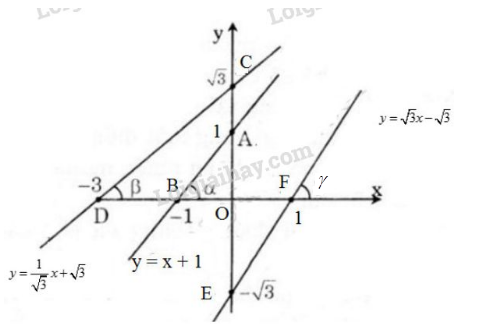
b)
Cách 1:
+ Đường thẳng có hệ số góc là
Suy ra
+ Đường thẳng có hệ số góc là
Suy ra
+ Đường thẳng có hệ số góc là
Suy ra
Cách 2:
+ Ta có:
, , .
+ Xét vuông tại
Thực hiện bấm máy tính:
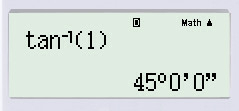
+ Xét vuông tại
+ Xét vuông tại
Lại có và là hai góc đối đỉnh .
Vậy .