Với tóm tắt lý thuyết Toán lớp 9 Hệ số góc của đường thẳng y = ax + b hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 9.

Toán 9 Bài 5: Hệ số góc của đường thẳng y = ax + b

A. Lý thuyết Hệ số góc của đường thẳng y = ax + b

I. Khái niệm

1. Góc tạo bởi đường thằng y = ax + b (a ≠ 0) với trục Ox.

Gọi A là giao điểm của đường thẳng y = ax + b với trục Ox và M là một điểm thuộc đường thẳng và có tung độ dương. Khi đó ∠MAx là góc tạo bởi đường thẳng y = ax + b với trục Ox.

2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0).

* Các đường thẳng có cùng hệ số a ( a là hệ số của x) thì tạo với trục Ox các góc bằng nhau.

Khi a > 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn 90°.

Khi a < 0 góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù và nếu a càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn 180°.

Như vậy, góc tạo bởi đường thẳng y = ax + b và trục Ox phụ thuộc vào a.

Người ta gọi a là hệ số góc của đường thẳng y = ax + b.

Chú ý:

Đường thẳng y = ax + b cắt 2 trục tọa độ tại 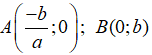 nên

    + Khi a > 0, ta có:

Từ đó dùng bảng lượng giác hoặc máy tính bỏ túi suy ra số đo của ∠MAx.

    + Khi a < 0 ta có:

Từ đó tìm số đo của góc (180° - ∠MAx), sau đó suy ra ∠MAx.

    + Các đường thẳng có cùng hệ số a (a là hệ số của x) thì tạo với trục Ox các góc bằng nhau.

    + Khi b = 0, ta có hàm số y = ax. Trong trường hợp này, ta có thể nói a là hệ số góc của đường thẳng y = ax

II. Ví dụ cụ thể

Câu 1: Cho hàm số y = x + 2. Tính góc tạo bởi đường thẳng y = x + 2 với trục Ox (làm tròn đến phút)

Hướng dẫn:

Vẽ đồ thị hàm số y = x + 2

Cho x = 0 thì y = 2 ta được điểm A (0; 2)

Cho y = 0 thì x = -2 ta được điểm B (-2; 0).

Đồ thị hàm số đã cho đi qua hai điểm A(0; 2); B(-2; 0).

Gọi góc tạo bởi đường thẳng y = x + 2 với trục Ox là α, ta có ∠ABO = α Xét tam giác vuông OAB , ta có 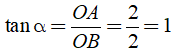 (1 chính là hệ số góc của đường thẳng y = x + 2)

Khi đó số đo góc α là α = 45°

Câu 2: Cho (d): y = ax + b . Tìm a, b biết (d) đi qua gốc tọa độ và song song với (d') trong đó (d') có hệ số góc bằng 1.

Giải:

Theo bài ta, (d) đi qua gốc tọa độ nên ta có b = 0

(d) song song với (d') và (d') có hệ số góc bằng 1 nên a = 1

Vậy a = 1, b = 0.

B. Bài tập tự luận

Câu 1: Cho các điểm và nằm trên đường thẳng có hệ số góc là . Tìm giá trị của m

Lời giải

Đường thẳng d có hệ số góc là m có nên có dạng: (d): y = mx + n A và B là hai điểm thuộc đường thẳng d nên ta có: 

Câu 2: Chứng minh rằng nếu một đường thẳng đi qua điểm A(x₁; y₁) và có hệ số góc bằng a thì đường thẳng đó có phương trình là y - y₁ = a(x - x₁)

Lời giải

Đường thẳng d có hệ số góc là a nên có dạng là (d):y = ax + b (d) đi qua điểm A(x₁; y₁) nên y₁ = ax₁ + b ⇒ b = y₁ - ax₁ Do đó: (d):y = ax + (y₁ - ax₁ ) hay (d): y - y₁ = a(x - x₁ ) (đpcm)