Cho hai hàm số y = 2x và y = −2x. Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho

Thanh Trà Ngày: 13-10-2022 Lớp 9

1.8 K

Với giải Bài 3 trang 45 Toán lớp 9 chi tiết trong Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số

Bài 3 trang 45 SGK Toán 9 Tập 1: Cho hai hàm số

y = 2 x

và

y = - 2 x

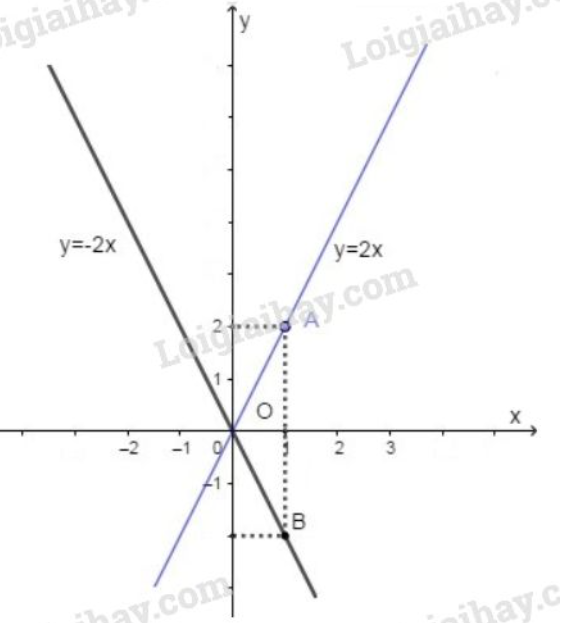
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.

b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?

Phương pháp giải:

a) Cách vẽ đồ thị hàm số $y = a x, (a \neq 0)$ : Cho $x = x_{0} \Rightarrow y_{0} = a x_{0}$

Đồ thị hàm số $y = a x (a \neq 0)$ là đường thẳng đi qua gốc tọa độ và điểm $A (x_{0}; y_{0})$

b) Với $x_{1}, x_{2} \in R$ :

Nếu $x_{1} < x_{2}$ và $f (x_{1}) < f (x_{2})$ thì hàm số $y = f (x)$ đồng biến trên $R$ .

Nếu $x_{1} < x_{2}$ và $f (x_{1}) > f (x_{2})$ thì hàm số $y = f (x)$ nghịch biến trên $R$ .

Lời giải:

+) Hàm số:

Cho $x = 0 \Rightarrow y = 2.0 = 0 \Rightarrow O (0; 0)$ .

Cho $x = 1 \Rightarrow y = 2.1 = 2 \Rightarrow A (1; 2)$ . $y = 2 x$

Đồ thị của hàm số $y = 2 x$ là đường thẳng đi qua $O (0; 0)$ và điểm $A (1; 2)$ .

+) Hàm số: $y = - 2 x$

Cho $x = 0 \Rightarrow y = - 2.0 = 0 \Rightarrow O (0; 0)$ .

Cho $x = 1 \Rightarrow y = - 2.1 = - 2 \Rightarrow B (1; - 2)$ .

Đồ thị của hàm số $y = - 2 x$ là đường thẳng đi qua $O (0; 0)$ và điểm $B (1; - 2)$ .

Giải Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số (ảnh 6)

b) Cách 1: Dùng định nghĩa

+) Xét hàm số: $y = f (x) = 2 x$

Với mọi $x_{1}, x_{2} \in R$

Giả sử $x_{1} < x_{2} \Rightarrow 2 x_{1} < 2 x_{2} \Rightarrow f (x_{1}) < f (x_{2})$

Do đó hàm số $y = 2 x$ là hàm số đồng biến trên $R$ .

+) Xét hàm số $y = g (x) = - 2 x$

Với mọi $x_{1}, x_{2} \in R$

Giả sử $x_{1} < x_{2} \Rightarrow - 2 x_{1} > - 2 x_{2} \Rightarrow g (x_{1}) > g (x_{2})$

Do đó hàm số $y = - 2 x$ là hàm số nghịch biến trên $R$ .

Cách 2:

Lập bảng giá trị cho $x$ nhận các giá trị $- 2; - 1; 0; 1; 2$ ta được bảng sau:

Giải Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số (ảnh 7)

Quan sát bảng trên ta thấy: Khi $x$ càng tăng thì giá trị của hàm số $y = 2 x$ càng tăng và giá trị của hàm số $y = - 2 x$ càng giảm. Do đó:

Hàm số $y = - 2 x$ nghịch biến, hàm số $y = 2 x$ đồng biến.

Từ khóa :

toán 9 Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

170

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

117

Tìm kiếm