Với lời giải SBT Toán 10 trang 80 Tập 2 chi tiết trong Bài tập cuối chương 9 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 9

Bài 11 trang 80 SBT Toán 10 Tập 2: Viết phương trình chính tắc của elip thoả mãn các điều kiện sau:

a) Độ đài trục lớn 26; độ dài trục nhỏ 10;

b) Độ dài trục lớn 10; tiêu cự 6.

Lời giải:

a) Ta có 2a = 26 ⇒ a = 13; 2b = 10 ⇒ b = 5.

Suy ra phương trình chính tắc của Elip là: $\frac{x^2}{{13}^2}+\frac{y^2}{5^2}=1\iff \frac{x^2}{169}+\frac{y^2}{25}=1$ .

Vậy phương trình chính tắc của Elip là: $\frac{x^2}{169}+\frac{y^2}{25}=1$ .

b) Ta có 2a = 10 ⇒ a = 5; 2c = 6 ⇒ c = 3 và b =  $\sqrt{a^2-c^2}=\sqrt{5^2-3^2}=4$

Suy ra phương trình chính tắc của Elip là: $\frac{x^2}{5^2}+\frac{y^2}{4^2}=1\iff \frac{x^2}{25}+\frac{y^2}{16}=1$ .

Vậyphương trình chính tắc của Elip là: $\frac{x^2}{25}+\frac{y^2}{16}=1$ .

Bài 12 trang 80 SBT Toán 10 Tập 2: Tìm toạ độ các tiêu điểm; toạ độ các đỉnh; độ đài trục thực và trục ảo của các hypebol sau:

a) $\frac{x^2}{25}-\frac{y^2}{144}=1$ ;

b) $\frac{x^2}{16}-\frac{y^2}{9}=1$

Lời giải:

a)$\frac{x^2}{25}-\frac{y^2}{144}=1\iff \frac{x^2}{5^2}-\frac{y^2}{{12}^2}=1$

Suy ra a = 5; b = 12 và $c=\sqrt{a^2+b^2}=\sqrt{5^2+{12}^2}=13$ .

Toạ độ các đỉnh A₁(- 5; 0); A₂(5; 0)

Tiêu điểm F₁(- 13; 0); F₂(13; 0)

Độ dài trục thực 2a = 10; độ dài trục ảo 2b = 24.

b)$\frac{x^2}{16}-\frac{y^2}{9}=1\iff \frac{x^2}{4^2}-\frac{y^2}{3^2}=1$

Suy ra a = 4; b = 3 và  $c=\sqrt{a^2+b^2}=\sqrt{4^2+3^2}=5$

Khi đó:

Toạ độ các đỉnh A₁(- 4; 0); A₂(4; 0);

Tiêu điểm F₁(- 5; 0); F₂(5; 0).

Độ dài trục thực 2a = 8; độ dài trục ảo 2b = 6.

Bài 13 trang 80 SBT Toán 10 Tập 2: Viết phương trình chính tắc của hypebol thoả mãn các điều kiện sau:

a) Đỉnh (-6; 0) và (6; 0); tiêu điểm (-10; 0) và (10; 0);

b) Độ dài trục thực là 10; độ dài trục ảo là 20.

Lời giải:

a) Ta có các đỉnh A₁(- 6; 0); A₂(6; 0) $\Rightarrow$  a = 6

Các tiêu điểm F₁(- 10; 0); F₂(10; 0) $\Rightarrow$  c = 10

$\Rightarrow$ b =  $\sqrt{c^2-a^2}=\sqrt{{10}^2-6^2}=8$

Khi đó phương trình chính tắc của Hypebol là: $\frac{x^2}{6^2}-\frac{y^2}{8^2}=1\iff \frac{x^2}{36}-\frac{y^2}{64}=1$ .

Vậy phương trình chính tắc của Hypebol là: $\frac{x^2}{36}-\frac{y^2}{64}=1$ .

b) Ta có:

Độ dài trục thực 2a = 10 $\Rightarrow$  a = 5;

Độ dài trục ảo 2b = 20 $\Rightarrow$  b = 10.

Khi đó phương trình chính tắc của Hypebol là: $\frac{x^2}{5^2}-\frac{y^2}{{10}^2}=1\iff \frac{x^2}{25}-\frac{y^2}{100}=1$ .

Vậy phương trình chính tắc của Hypebol là: $\frac{x^2}{25}-\frac{y^2}{100}=1$ .

Bài 14 trang 80 SBT Toán 10 Tập 2: Tìm toạ độ tiêu điểm, phương trình đường chuẩn của các parabol sau:

a) y² = 4x;

b) y² = 2x;

c) y² = – 6x.

Lời giải:

a) Xét parabol y² = 4x

Ta có 2p = 4 ⇔ p = 2 suy ra tiêu điểm F(1; 0) và đường chuẩn ∆: x + 1 = 0.

b) Xét parabol y² = 2x

Ta có 2p = 2 ⇔ p = 1 suy ra tiêu điểm $F\left(\frac{1}{2};0\right)$  và đường chuẩn ∆: $x+\frac{1}{2}=0$ .

c) Xét parabol y² = – 6x

Ta có 2p = – 6 ⇔ p = – 3 suy ra tiêu điểm $F\left(-\frac{3}{2};0\right)$  và đường chuẩn ∆: $x-\frac{3}{2}=0$ .

Bài 15 trang 80 SBT Toán 10 Tập 2: Viết phương trình chính tắc của parabol thoả mãn các điều kiện:

a) Tiêu điểm (8; 0);

b) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 4.

Lời giải:

a) Ta có tiêu điểm F(8; 0) nên $\frac{p}{2}=8$  ⇒ p = 16

Vì vậy phương trình chính tắc của Parabol: y² = 32x.

b) Ta có khoảng cách từ tiêu điểm đến đường chuẩn bằng 4 nên p = 4

Vì vậy phương trình chính tắc của Parabol: y² = 8x.

Bài 16 trang 80 SBT Toán 10 Tập 2: Một nhà mái vòm có mặt cắt hình nửa elip cao 6 m rộng l6 m.

a) Hãy chọn hệ toạ độ thích hợp và viết phương trình của elip nói trên;

b) Tính khoảng cách thẳng đứng từ một điểm cách chân vách 4 m lên đến mái vòm.

Lời giải:

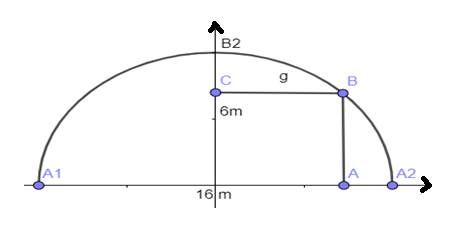
a) Giả sử mái nhà vòm có dạng như hình vẽ, ta có:

2a = 16 $\Rightarrow$  a = 8 và b = 6

Phương trình chính tắc của Elip là: $\frac{x^2}{8^2}+\frac{y^2}{6^2}=1\iff \frac{x^2}{64}+\frac{y^2}{36}=1$ .

b) Gọi điểm A là điểm có khoảng cách 4m từ chân vách nên OA = 8 – 4 = 4 m. Từ điểm A dõng lên cắt mái vòm tại B khi đó B(4; y).

Suy ra độ dài AB là khoảng cách từ chân vách đến mái vòm và bằng y.

Vì B thuộc Elip nên ta có $\frac{4^2}{64}+\frac{y^2}{36}=1\iff y=\sqrt{36\left(1-\frac{4^2}{64}\right)}=3\sqrt{3}$ .

Vậy khoảng cách từ điểm cách chân vách 4m lên đến mái vòm là $3\sqrt{3}$  ≈ 5,2 m.

Bài 17 trang 80 SBT Toán 10 Tập 2: Cho biết Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là elip (E) với Trái Đất là một tiêu điểm. Cho biết độ dài hai trục của (E) là 768800 km và 767619 km. Viết phương trình chính tắc của elip (E).

Lời giải:

Ta có:

2a = 768800 $\Rightarrow$  a = 384400;

2b = 767619 $\Rightarrow$  b = $\frac{767619}{2}$ .

Khi đó phương trình chính tắc của Elip là: $\frac{x^2}{{384400}^2}+\frac{4y^2}{{767619}^2}=1$ .

Bài 18 trang 80 SBT Toán 10 Tập 2: Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là 50 cm; chiều sâu của gương là 40 cm. Viết phương trình chính tắc của (P).

Lời giải:

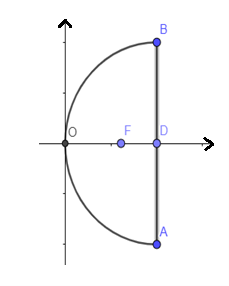
Ta có OD = 40 cm; AB = 50 cm

Gọi phương trình chính tắc của parabol là y² = 2px

Dựa vào hình vẽ ta có khi x = 40 thì y = 25

$\Rightarrow$ 25² = 2.p.40 $\Rightarrow$  p =  $\frac{125}{16}$

Phương trình chính tắc của parabol là: y² = $\frac{125}{8}$ x.

Bài 19 trang 80 SBT Toán 10 Tập 2: Màn hình của rađa tại trạm điều khiển không lưu được thiết lập hệ toạ độ Oxy với vị trí trạm có toạ độ O(0; 0) và rađa có bán kính hoạt động là 600 km. Một máy bay khởi hành tử sân bay lúc 8 giờ. Cho biết sau t giờ máy bay có toạ độ: $\left\{\begin{array}{c}x=l+180t\\ y=1-180t\end{array}\right.$ .

a) Tìm toạ độ máy bay lúc 9 giờ;

b) Tính khoảng cách giữa máy bay và trạm điều khiển không lưu;

c) Lúc mây giờ máy bay ra khỏi tầm hoạt động của rađa?

Lời giải:

a) Máy bay khởi hành lúc 8 giờ vậy lúc 9 giờ máy bay bay được 1 giờ hay t = 1 nên toạ độ của máy báy là:

 $\left\{\begin{array}{l}x=1+180\\ y=1-180\end{array}\right.\iff \left\{\begin{array}{l}x=181\\ y=-179\end{array}\right.$

Vậy toạ độ máy bay lúc 9 giờ là: A(181; – 179).

b) Khoảng cách giữa máy bay và trạm không điều khiển bằng OA

Ta có OA = $\sqrt{{(x_A-x_O)}^2+{(y_A-y_O)}^2}=\sqrt{{(181-0)}^2+{(-179-0)}^2}=\sqrt{64802}$  $\approx$  255 km.

Vậy khoảng cách giữa máy bay và trạm không điều khiển khoảng 255 km.

c) Sau t giờ máy bay có toạ độ:$\left\{\begin{array}{c}x=l+180t\\ y=1-180t\end{array}\right.$

Hay toạ độ máy bay sau t giờ là: B(1 + 180t; 1 – 180t).

Để máy bay ra khỏi tầm hoạt động của rađa thì OB > 600 km ⇔ OB² > 600²

Ta có OB² =  (x_B – x_O)² + (y_B – y_O)² = (1 + 180t)² + (1 – 180t)² > 600²

⇔ 32400t² + 360t +1 + 32400t² – 360t +1 > 600²

⇔ 64800t² – 359998 > 0

⇒ |t| > 2,36

Mà t > 0 nên t > 2,36

Ta lại có 2,36 giờ ≈ 2 giờ 22 phút.

Vậy lúc khoảng 10 giờ 22 phút trở đi máy bay ra khỏi tầm hoạt động của rađa.

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 77 Tập 2

Giải SBT Toán 10 trang 78 Tập 2

Giải SBT Toán 10 trang 79 Tập 2

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài tập cuối chương 10