Với giải sách bài tập Toán 10 Bài tập cuối chương 8 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 8

Giải SBT Toán 10 trang 48 Tập 2

A. TRẮC NGHIỆM

Câu 1 trang 48 SBT Toán 10 Tập 2: Một nhóm có 4 học sinh, mỗi học sinh chọn một trong ba lớp môn thể thao: bóng đá, bóng rổ và cầu lông. Có bao nhiêu kết quả khác nhau về sự chọn của các học sinh trong nhóm?

A. 3⁴;

B. 4³;

C. 3!;

D. 4!.

Lời giải:

Đáp án đúng là A

Một học sinh có 3 cách chọn lớp thể thao. Áp dụng quy tắc nhân ta có 4 học sinh có 3.3.3.3 = 3⁴ kết quả khác nhau về sự chọn của các học sinh trong nhóm

Câu 2 trang 48 SBT Toán 10 Tập 2: 90.91..... 100 bằng:

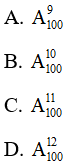
Lời giải:

Đáp án đúng là C

M = 90.91..... 100 = 100. ( 100 – 1 ) . ( 100 – 2 )... ( 100 – 11 + 1 )

M = $A_{100}^{11}$

Vậy đáp án đúng là C.

Câu 3 trang 48 SBT Toán 10 Tập 2: Một tập hợp có 10 phần tử. Tập hợp này có bao nhiêu tập hợp con có 3 phần tử?

A.3!;

B.10.9.8,

C. 10³,

D. $\frac{10!}{3!7!}$.

Lời giải:

Đáp án đúng là D

Số tập hợp con có 3 phần tử trong số 10 phần tử là tổ hợp chập 3 của 10 phần tử hay

Câu 4 trang 48 SBT Toán 10 Tập 2: Một tập hợp có 5 phần tử. Tập hợp này có bao nhiêu tập hợp con có nhiều nhất 2 phần tử?

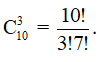
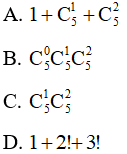
Lời giải:

Đáp án đúng là A

Trường hợp 1: Có 1 tập hợp con có 0 phần tử.

Trường hợp 2: Số tập hợp con có 1 phần tử là tổ hợp chập 1 của 5 phần tử hay $C_5^1$.

Trường hợp 3: Số tập hợp con có 2 phần tử là tổ hợp chập 2 của 5 phần tử hay $C_5^2$.

Theo quy tắc cộng ta có $1+C_5^1+C_5^2$ tập hợp con có nhiều nhất 2 phần tử.

Câu 5 trang 48 SBT Toán 10 Tập 2: Trong khai triển ${\left(\sqrt{x}-2\right)}^5$, hệ số của ($\sqrt{x}$)⁴ bằng:

A. -5;

B. 5;

C. -10;

D. 10.

Lời giải:

Đáp án đúng là C

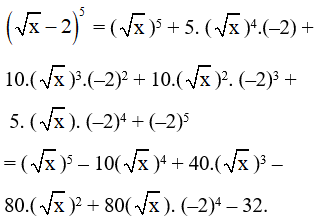
Vậy hệ số của ($\sqrt{\text{x}}$)⁴ trong khai triển đã cho là – 10.

B. TỰ LUẬN

Bài 1 trang 48 SBT Toán 10 Tập 2: Một bài kiểm tra có 6 câu hỏi trắc nghiệm, mỗi câu có 4 phương án chọn. Nếu chọn một cách tuỳ ý một phương án cho mỗi câu hỏi thì có bao nhiêu cách hoàn thành bài kiểm tra?

Lời giải:

Mỗi câu có 4 phương án chọn. Áp dụng quy tắc nhân ta có 6 câu hỏi có 4⁶  = 4096 cách hoàn thành bài kiểm tra.

Bài 2 trang 48 SBT Toán 10 Tập 2: Chợ Bến Thành có 4 cổng ra vào. Một người đi chợ ở chợ này thì,

a) có bao nhiêu cách vào và ra chợ?

b) có bao nhiêu cách vào và ra chợ bằng hai cổng khác nhau?

Lời giải:

a) Có 4 cách chọn cổng để vào chợ và có 4 cách chọn cổng để ra chợ. Áp dụng quy tắc nhân ta có 4.4 = 16 cách vào và ra chợ.

b) Có 4 cách chọn cổng để vào chợ và có 3 cách chọn cổng để ra chợ khác với cổng vào. Áp dụng quy tắc nhân ta có 4.3 = 12 cách vào và ra chợ bằng hai cổng khác nhau.

Bài 3 trang 48 SBT Toán 10 Tập 2: Chọn 3 cuốn từ 6 cuốn sách khác nhau và đưa cho 3 bạn cùng lớp, mỗi bạn l cuốn. Có bao nhiêu cách thực hiện việc này?

Lời giải:

Chọn 3 cuốn từ 6 cuốn sách khác nhau và đưa cho 3 bạn cùng lớp, mỗi bạn l cuốn là chỉnh hợp chập 3 của 6 cuốn sách hay ${\text{A}}_{\text{6}}^{\text{3}}$ = 120 cách.

Bài 4 trang 48 SBT Toán 10 Tập 2: Từ một danh sách gồm 9 người, người ta bầu ra một uỷ ban gồm một chủ tịch, một phó chủ tịch và 3 uỷ viên. Có bao nhiêu khả năng có thể về kết quả bầu uỷ ban này?

Lời giải:

Có 9 cách bầu ra 1 chủ tịch trong 9 người.

Có 8 cách bầu ra 1 phó chủ tịch trong 8 người còn lại (trừ người đã được bầu làm chủ tịch ).

Có ${\text{C}}_{\text{7}}^{\text{3}}$ cách bầu ra 3 ủy viên trong 7 người còn lại ( trừ chủ tịch và phó chủ tịch ).

Áp dụng quy tắc nhân ta có 9.8. ${\text{C}}_{\text{7}}^{\text{3}}$ = 9.8.35 = 2520.

Vậy có tất cả 2 520 khả năng về kết quả bầu ủy ban này.

Giải SBT Toán 10 trang 49 Tập 2

Bài 5 trang 49 SBT Toán 10 Tập 2: Trên một trạm quan sát, có sẵn 4 lá cờ màu khác nhau (đỏ, xanh, vàng, cam). Mỗi khi muốn báo một tín hiệu, chiến sĩ thông tin lấy 2 hoặc 3 trong số 4 lá cờ đó và cắm thành một hàng trên nóc của trạm. Bao nhiêu tín hiệu khác nhau có thể được tạo ra?

Lời giải:

Trường hợp 1: Có 2 lá cờ được cắm. Cách chọn 2 màu cờ và sắp xếp 2 lá cờ là chỉnh hợp chập 2 của 4 lá cờ. Có ${\text{A}}_{\text{4}}^{\text{2}}$ tín hiệu được tạo ra.

Trường hợp 2: Có 3 lá cờ được cắm. Cách chọn 3 màu cờ và sắp xếp 3 lá cờ là chỉnh hợp chập 3 của 4 lá cờ. Có ${\text{A}}_{\text{4}}^{\text{3}}$ tín hiệu được tạo ra.

Áp dụng quy tắc cộng ta có ${\text{A}}_{\text{4}}^{\text{2}}$ + ${\text{A}}_{\text{4}}^{\text{3}}$ = 12 + 24 = 36 tín hiệu khác nhau có thể được tạo ra.

Bài 6 trang 49 SBT Toán 10 Tập 2: Giả sử (2x + 1)⁴ = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴. Hãy tính:

a) a₀ + a₁ + a₂ + a₃ + a₄;

b) a₁ + a₂ + a₃ + a₄.

Lời giải:

a) Ta có: (2x + 1)⁴ = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴.

Chọn x = 1, ta được:

(2.1 + 1)⁴ = a₀ + a₁.1 + a₂.1² + a₃.1³ + a₄.1⁴

⇔ 3⁴ = a₀ + a₁ + a₂ + a₃ + a₄

⇔ a₀ + a₁ + a₂ + a₃ + a₄ = 81

Vậy a₀ + a₁ + a₂ + a₃ + a₄ = 81.

b) Ta có: (2x + 1)⁴ = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴.

Chọn x = 0, ta được:

(2.0 + 1)⁴ = a₀ + a₁.0 + a₂.0² + a₃.0³ + a₄.0⁴

⇔ 1⁴ = a₀

⇔ a₀ = 1

Mà a₀ + a₁ + a₂ + a₃ + a₄ = 81

⇒ a₁ + a₂ + a₃ + a₄ = 81 – a₀ = 81 – 1 = 80.

Vậy a₁ + a₂ + a₃ + a₄ = 80.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Nhị thức Newton

Bài 1: Tọa độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng tọa độ

Bài 3: Đường tròn trong mặt phẳng tọa độ

Lý thuyết Chương 8: Đại số tổ hợp

1. Quy tắc cộng

– Giả sử một công việc có thể được thực hiện theo phương án A hoặc B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.

Ví dụ: Lớp 10A có 20 học sinh, lớp 10C có 24 học sinh. Có bao nhiêu cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường?

Hướng dẫn giải

Công việc cử 1 học sinh đi có 2 phương án thực hiện:

Phương án 1: Cử 1 học sinh của lớp 10A, ta có 20 cách.

Phương án 2: Cử 1 học sinh của lớp 10C, ta có 24 cách.

Ta thấy mỗi cách thực hiện của phương án B đều không trùng với cách của phương án A. Do đó theo quy tắc cộng, có 20 + 24 = 44 cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường.

2. Quy tắc nhân

– Giả sử một công việc được chia thành hai công đoạn. Công đoạn thứ nhất có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó công việc có thể thực hiện theo m. n cách.

Ví dụ: Từ nhà An đến trường đi qua 3 điểm A, B, C. Từ nhà An đến điểm A có 3 cách đi, từ điểm A đến điểm B có 4 cách đi, từ điểm B đến điểm C có 2 cách đi. Từ điểm C đến trường học có 2 cách đi. Hỏi có bao nhiêu cách từ nhà An đến trường?

Hướng dẫn giải

Từ nhà An đến trường đi qua 3 điểm A, B, C, như vậy có 4 công đoạn:

+ Công đoạn 1: Từ nhà An đến điểm A có 3 cách đi.

+ Công đoạn 2: Từ điểm A đến điểm B có 4 cách đi

+ Công đoạn 3: Từ điểm B đến điểm C có 2 cách đi.

+ Công đoạn 4: Từ điểm C đến trường học có 2 cách đi.

Do đó, theo quy tắc nhân, có 3. 4. 2. 2 = 48 cách đi từ nhà An đến trường.

3. Hoán vị

– Cho tập hợp A có n phần tử (n ≥ 1).

Mỗi cách sắp xếp n phần tử của A theo một thứ tự gọi là một hoán vị các phần tử đó (gọi tắt là hoán vị của A hay của n phần tử).

Kí hiệu P_n là số hoán vị của n phần tử.

– Số các hoán vị của n phần tử (n ≥ 1) bằng:

P_n = n(n – 1)(n – 2)….2. 1.

Chú ý:

+ Ta đưa vào kí hiệu n! = n(n – 1)(n – 2)…. 2. 1 và đọc là n giai thừa hoặc giai thừa của n.

Khi đó  = n!.

+ Quy ước: 0! = 1.

Ví dụ: Có thể lập được bao nhiêu số có 6 chữ số khác nhau từ các chữ số 1; 2; 3; 5; 6; 7? Trong những số đó có bao nhiêu số lẻ?

Hướng dẫn giải

• Mỗi số tự nhiên có 6 chữ số khác nhau được lập từ 6 chữ số 1; 2; 3; 5; 6; 7 là một hoán vị của 6 chữ số này. Do đó, số số tự nhiên có 6 chữ số khác nhau lập được là:

$P_6$ = 6! = 6. 5. 4. 3. 2. 1 = 720 (số).

Vậy lập được 720 số.

Ta lập số tự nhiên lẻ có 6 chữ số khác nhau từ các chữ số 1; 2; 3; 5; 6; 7.

• Bước 1: Chọn chữ số hàng đơn vị là chữ số lẻ.

 Có 4 cách chọn (chọn một trong các chữ số 1; 3; 5; 7).

Bước 2: Chọn năm chữ số còn lại.

Có P₅ = 5! cách chọn.

Từ đó, theo quy tắc nhân, số số tự nhiên lẻ có sáu chữ số khác nhau lập từ các chữ số đã cho là:

4.5! = 480 (số).

4. Chỉnh hợp

– Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k với 1 ≤ k ≤ n.

Mỗi cách lấy k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.

Kí hiệu $A_n^k$  là số chỉnh hợp chập k của n phần tử.

– Số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) bằng:

$A_n^k$ = n(n – 1)(n – 2) ….(n – k + 1) = $\frac{n!}{\left(n-k\right)!}$ .

Nhận xét: Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó.

Ta có $P_n=A_n^n$ , n ≥ 1.

Ví dụ: Trên bàn có 10 quả cam to nhỏ khác nhau. Chọn 3 quả cam trong 10 quả đó, và đặt mỗi quả vào một giỏ nhựa khác nhau. Hỏi có bao nhiêu cách chọn 3 quả cam đó.

Hướng dẫn giải

Mỗi cách chọn 3 quả cam trong 10 quả cam đó và đặt vào 3 giỏ nhựa được gọi là một chỉnh hợp chập 3 của 10 quả cam. Ta thấy số các chỉnh hợp này bằng:

$A_{10}^3$ = 10. 9. 8 = 720.

Vậy có 720 cách chọn 3 quả cam đó.

5. Tổ hợp

– Cho tập hợp A có n phần tử (n ≥ 1).

Mỗi tập con gồm k phần tử (1 ≤ k ≤ n) của A được gọi là một tổ hợp chập k của n phần tử.

Kí hiệu $C_n^k$  là số tổ hợp chập k của n phần tử (1 ≤ k ≤ n).

– Số các tổ hợp chập k của n phần tử (1 ≤ k ≤ n) bằng:

 $C_n^k$ = $\frac{n!}{k!\left(n-k\right)!}$ .

Chú ý: Người ta quy ước $C_n^0=1$ .

Nhận xét: $C_n^k=C_n^{n-k}$  (0 ≤ k ≤ n).

Ví dụ: Lớp 10A có 20 học sinh. Trong tuần sau có 5 bạn được cử đi dự đại hội Đoàn Thanh niên. Hỏi có bao nhiêu cách chọn 5 bạn học sinh trong lớp đi dự đại hội Đoàn Thanh niên?

Hướng dẫn giải

Mỗi cách chọn 5 bạn học sinh trong lớp từ 20 bạn học sinh là một tổ hợp chập 5 của 20 học sinh. Do đó số cách chọn 5 bạn học sinh trong lớp đi dự đại hội Đoàn Thanh niên là:

$C_{20}^5=\frac{20!}{5!.15!}$ = 15 504 (cách).

Vậy có 15 504 cách chọn 5 bạn học sinh trong lớp đi dự đại hội Đoàn Thanh niên.

Ví dụ: Tính:

a) $C_{14}^{11};$

b) $C_{24}^{22}+C_{24}^2;$

c) $C_{27}^2-C_{26}^2.$

Hướng dẫn giải

a) $C_{14}^{11}=\frac{14!}{11!.3!}=\frac{\mathrm{14.13.12.11}!}{11!\mathrm{.3.2.1}}=\frac{\mathrm{14.13.12}}{\mathrm{3.2.1}}=364.$

b) $C_{24}^{22}+C_{24}^2=C_{24}^{24-2}+C_{24}^2=C_{24}^2+C_{24}^2=2C_{24}^2$

$=2.\frac{24!}{2!.22!}=2.\frac{\mathrm{24.23.22}!}{\mathrm{2.1.22}!}=24.23=552.$

c) $C_{27}^2-C_{26}^2=\frac{27!}{2!.25!}-\frac{26!}{2!.24!}=\frac{\mathrm{27.26.25}!}{\mathrm{2.1.25}!}-\frac{\mathrm{26.25.24}!}{\mathrm{2.1.24}!}$

$=\frac{27.26}{2.1}-\frac{26.25}{2.1}=\frac{26}{2}.\left(27-25\right)=13.2=26.$

6. Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay

Với một số máy tính cầm tay, ta có thể tính toán nhanh các số các hoán vị, chỉnh hợp và tổ hợp.

Ví dụ:

• Để tính $P_{10}$  ta ấn liên tiếp các phím:

$\boxed{10}\boxed{SHIFT}\boxed{x^{-1}}\left(x!\right)\boxed{=}$

Ta nhận được kết quả là 3 628 800.

• Để tính $A_6^4$  ta ấn liên tiếp các phím:

$\boxed{6}\boxed{SHIFT}\boxed{\times }\left(n\mathrm{Pr}\right)\boxed{4}\boxed{=}$

Ta nhận được kết quả là 360.

• Để tính $C_8^4$  ta ấn liên tiếp các phím:

$\boxed{8}\boxed{SHIFT}\boxed{÷}\left(nCr\right)\boxed{4}\boxed{=}$

Ta nhận được kết quả là 70.

7. Nhị thức Newton

Hai công thức khai triển:

• ${\left(a+b\right)}^4=C_4^0{a}^4+C_4^1{a}^{3}b+C_4^2{a}^2{b}^2+C_4^{3}a{b}^3+C_4^4{b}^4$

$=a^4+4a^{3}b+6a^2{b}^2+4a{b}^3+b^4;$

•  ${\left(a+b\right)}^5=C_5^0{a}^5+C_5^1{a}^{4}b+C_5^2{a}^3{b}^2+C_5^3{a}^2{b}^3+C_5^{4}a{b}^4+C_5^5{b}^5$

$=a^5+5a^{4}b+10a^3{b}^2+10a^2{b}^3+5a{b}^4+b^5.$

Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ${\left(a+b\right)}^n$  ứng với n = 4 và n = 5.

Chú ý:

– Các hệ số trong khai triển nhị thức Newton (a + b)ⁿ với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.

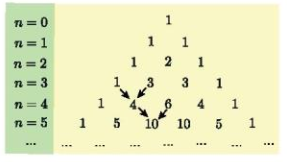
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).

Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).

Ví dụ: Sử dụng công thức nhị thức Newton khai triển biểu thức (a + 2)⁴.

Hướng dẫn giải

Theo công thức nhị thức Newton ta có:

(a + 2)⁴ = 1.a⁴ + 4a³.2 + 6a².2² + 4a.2³ + 2⁴

= a⁴ + 8a³ + 24a² + 32a + 16.

Ví dụ: Khai triển và rút gọn biểu thức: ${\left(1+\sqrt{5}\right)}^5+{\left(1-\sqrt{5}\right)}^5.$

Hướng dẫn giải

Theo công thức nhị thức Newton ta có:

•${\left(1+\sqrt{5}\right)}^5=1+5\sqrt{5}+10.{\left(\sqrt{5}\right)}^2+10.{\left(\sqrt{5}\right)}^3+5.{\left(\sqrt{5}\right)}^4+1.{\left(\sqrt{5}\right)}^5$

$=1+5\sqrt{5}+50+50\sqrt{5}+125+25\sqrt{5}$

$=176+80\sqrt{5}.$

•${\left(1+\sqrt{5}\right)}^5=1+5\left(-\sqrt{5}\right)+10.{\left(-\sqrt{5}\right)}^2+10.{\left(-\sqrt{5}\right)}^3+5.{\left(-\sqrt{5}\right)}^4+1.{\left(-\sqrt{5}\right)}^5$

$=1-5\sqrt{5}+50-50\sqrt{5}+125-25\sqrt{5}$

$=176-80\sqrt{5}.$

Do đó ta có: ${\left(1+\sqrt{5}\right)}^5+{\left(1-\sqrt{5}\right)}^5=176+80\sqrt{5}+176-80\sqrt{5}=352.$