Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 3: Bất phương trình một ẩn hay, chi tiết giúp học sinh dễ dàng làm bài tập Bất phương trình một ẩn lớp 8.

Giải bài tập Toán lớp 8 Bài 3: Bất phương trình một ẩn

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 41 Toán 8 Tập 2: a) Hãy cho biết vế trái, vế phải của bất phương trình x² ≤ 6x – 5;

b) Chứng tỏ các số 3; 4 và 5 đều là nghiệm, còn số 6 không phải là nghiệm của bất phương trình vừa nêu.

Lời giải

a) Vế trái của bất phương trình là x²;

Vế phải của bất phương trình là 6x – 5.

b)

+ Với x = 3, BPT trở thành 3² ≤ 6.3 – 5 hay 9 ≤ 13 (đúng)

Do đó x = 3 là nghiệm của bất phương trình.

+ Với x = 4, BPT trở thành: 4² ≤ 6.4 – 5 hay 16 ≤ 19 (Đúng)

Do đó x = 4 là nghiệm của bất phương trình.

+ Với x = 5, BPT trở thành 5² ≤ 6.5 – 5 hay 25 ≤ 25 (Đúng)

Do đó x = 5 là nghiệm của bất phương trình

+ Với x = 6 , BPT trở thành: 6² ≤ 6.6 –5 hay 36 ≤ 31 (vô lí)

Do đó x = 6 không là nghiệm của bất phương trình.

Câu hỏi 2 trang 42 Toán 8 Tập 2: Hãy cho biết vế trái, vế phải và tập nghiệm của bất phương trình x > 3, bất phương trình 3 < x và phương trình x = 3.

Lời giải:

- Bất phương trình x > 3 có VT = x; VP = 3

Nghiệm của bất phương trình x > 3 là tập hợp A gồm các số lớn hơn 3, hay tập A gồm các phần tử x sao cho A = {x | x > 3}.

- Bất phương trình 3 < x có VT = 3; VP = x

Nghiệm của bất phương trình 3 < x là tập hợp A gồm các số lớn hơn 3, hay tập A gồm các phần tử x sao cho A = {x | x > 3}.

- Phương trình x = 3 có VT = x; VP = 3

Nghiệm của phương trình x = 3 là 3.

Câu hỏi 3 trang 42 Toán 8 Tập 2: Viết và biểu diễn tập nghiệm của bất phương trình x ≥ -2 trên trục số.

Hướng dẫn: Trên trục số, gạch bỏ các điểm bên trái điểm -2 bằng các dấu “/” và giữu lại điểm – 2 bằng dấu “[“.

Lời giải:

Tập nghiệm của bất phương trình x ≥ -2 là S = {x | x ≥ -2}

Biểu diễn trên trục số:

Câu hỏi 4 trang 42 Toán 8 Tập 2: Viết và biểu diễn tập nghiệm của bất phương trình x < 4 trên trục số.

Hướng dẫn: Trên trục số, gạch bỏ các điểm bên phải điểm 4 bằng các dấu “/” và gạch bỏ điểm 4 bằng dấu “)”.

Lời giải:

Tập nghiệm của bất phương trình x < 4 là S = {x| x < 4}

Biểu diễn trên trục số:

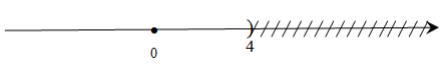
Bài tập (trang 43)

Bài 15 trang 43 Toán 8 Tập 2: Kiểm tra xem giá trị x = 3 là nghiệm của bất phương trình nào trong các bất phương trình sau:

a) 2x + 3 < 9;

b) -4x > 2x + 5;

c) 5 - x > 3x – 12.

Lời giải:

Thay x = 3 lần lượt vào từng vế của mỗi bất phương trình, ta được:

a) Vế trái = 2x + 3 = 2.3 + 3 = 9

Ta thấy 9 < 9 (vô lí)

Vậy x = 3 không là nghiệm của bất phương trình 2x + 3 < 9.

b)

Vế trái =  -4x = -4.3 = -12

Vế phải = 2x + 5 = 2.3 + 5 = 11

Vì -12 < 11 nên x = 3 không phải nghiệm của bất phương trình -4x > 2x + 5.

c)

Vế trái = 5 – x = 5 – 3 = 2

Vế phải = 3x – 12 = 3.3 – 12 = -3.

Vì 2 > -3 nên x = 3 là nghiệm của bất phương trình 5 – x > 3x – 12.

Bài 16 trang 43 Toán 8 Tập 2: Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:

a) x < 4 ;    

b) x ≤ -2;

c) x > -3 ;    

d) x ≥ 1.

Lời giải:

a) Tập nghiệm của bất phương trình x < 4 là S = {x| x < 4}.

Biểu diễn tập nghiệm trên trục số:

b) Tập nghiệm của bất phương trình x ≤ -2 là S = {x| x ≤ -2}.

Biểu diễn tập nghiệm trên trục số:

c) Tập nghiệm của bất phương trình x > -3 là S = {x | x > -3}

Biểu diễn tập nghiệm trên trục số:

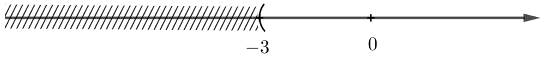
d) Tập nghiệm của bất phương trình x ≥ 1 là S = {x | x ≥ 1}.

Biểu diễn tập nghiệm trên trục số:

Bài 17 trang 43 Toán 8 Tập 2: Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).

Lời giải:

a) Ta thấy các điểm lớn hơn 6 trên hình a bị gạch bỏ và tại điểm 6 ta thấy kí hiệu “[“ nên hình a biểu diễn tập nghiệm của bất phương trình x ≤ 6.

b) Ta thấy các điểm nhỏ hơn 2 trên hình b bị gạch bỏ và tại điểm 2 ta thấy kí hiệu “(“ nên hình b biểu diễn tập nghiệm của bất phương trình x > 2.

c) Ta thấy các điểm nhỏ hơn 5 trên hình c bị gạch bỏ và tại điểm 5 ta thấy kí hiệu “[“  nên hình c biểu diễn tập nghiệm của bất phương trình x ≥ 5.

d) Ta thấy các điểm lớn hơn -1 trên hình d bị gạch bỏ và tại điểm -1 ta thấy kí hiệu “)” nên hình d biểu diễn tập nghiệm của bất phương trình x < -1.

Bài 18 trang 43 Toán 8 Tập 2: Hãy lập bất phương trình cho bài toán sau:

Quãng đường từ A đến B dài 50km. Một ô tô đi từ A đến B, khởi hành lúc 7h. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước 9 giờ cùng ngày?

Lời giải:

Gọi x là vận tốc của ô tô (x > 0, km/h)

Thời gian ô tô đi từ A đến B là:  $\frac{50}{x}$ (giờ).        

Để ô tô đến trước 9h thì ô tô phải đi với thời gian ít hơn: 9 - 7 = 2h hay  $\frac{50}{x}\text{\hspace{0.17em}}<2$

⇔ 50 < 2x (nhân cả hai vế với x > 0)

⇔ 25 < x (chia cả hai vế cho 2).

Vậy để ô tô đến B trước 9 giờ thì ô tô phải chạy với vận tốc x thỏa mãn: x > 25(km/h)