Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập Bất phương trình một ẩn Toán lớp 8, tài liệu bao gồm 4 trang đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Lý thuyết và bài tập Bất phương trình một ẩn gồm các nội dung chính sau:

I. Tóm tắt lý thuyết

- tóm tắt lý thuyết ngắn gọn.

II. Bài tập và các dạng bài toán

- gồm 3 dạng bài tập Lý thuyết và bài tập Bất phương trình một ẩn.

III. Bài tập tự luyện

- gồm 6 bài tập tự luyện giúp học sinh tự rèn luyện cách giải các dạng Lý thuyết và bài tập Bất phương trình một ẩn.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BẤT PHƯƠNG TRÌNH MỘT ẨN

I. TÓM TẮT LÝ THUYẾT

1. Bất phương trình một ẩn

Bất phương trình một ẩn x là bất phương trình có dạng:

$A\left(x\right)<B\left(x\right)$ hoặc  $A\left(x\right)>B\left(x\right)$

hoặc $A\left(x\right)\le B\left(x\right)$ hoặc  $A\left(x\right)\ge B\left(x\right)$

Trong đó A(x) là vế trái và B(x) là vế phải.

Ví dụ: $2x^2-5x+3\ge 0$ là một bất phương trình ẩn x

$\frac{1}{2}t-4<2t+3$ là một bất phương trình bậc nhất ẩn t.

2. Nghiệm của bất phương trình một ẩn

Giá trị x₀ được gọi là nghiệm của bất phương trình A(x) < B(x) nếu bất đẳng thức A(x₀) < B(x₀) đúng.

Tương tự đối với các dạng bất phương trình còn lại.

3. Giải bất phương trình một ẩn

Giải bất phương trình là đi tìm tập nghiệm  của bất phương trình đó.

4. Hai bất phương trình tương đương

Hai bất phương trình gọi là tương đương nếu chúng có cùng tập nghiệm

Chú ý: hai bất phương trình cùng vô nghiệm tương đương nhau.

II. BÀI TẬP VÀ CÁC DẠNG TOÁN

Dạng 1. Xét xem một số có là nghiệm của bất phương trình hay không?

Phương pháp giải: Để xem x₀ có là nghiệm của bất phương trình A(x) < B(x) hay không, ta thay x₀ vào bất phương trình để kiểm tra:

- Nếu bất đẳng thức thu được luôn đúng, ta nói x₀ là nghiệm của bất phương trình đã cho.

- Nếu bất đẳng thức thu được không đúng, ta nói x₀ không là nghiệm của bất phương trình đã cho.

1A. Hãy xét xem số x = 1 có là nghiệm của mỗi bất phương trình sau hay không?

a)  $\frac{2x}{3}+1\le x-2$                b)  $x^2-x+3>\frac{1}{3}{x}^3+2$

1B. Trong các giá trị y = 0 và y = -2, đâu là nghiệm của bất phương trình  $\frac{3}{(y-1)}+\left|y-3\right|\ge \sqrt{1+2y^2}+3y?$

2A. Cho bất phương trình $\sqrt{x+6}+m>\frac{x}{6}-3$. Tìm m để bất phương trình có nghiệm x = 3.

2B. Tìm a để bất phương trình $\frac{1}{6}\sqrt{2t^2+4}+a<\frac{3}{2(t+1)}-2t^2+1$ nhận là nghiệm.

Dạng 2. Viết bằng kí hiệu tập hợp và biểu diễn tập nghiệm của bất phương trình trên trục số.

Phương pháp giải; Thực hiện theo các bước sau:

Bước 1. Vẽ trục số và điền các giá trị 0, giá trị nghiệm của bất phương tình trên trục số.

Bước 2.  Gạch bỏ phần không thuộc tập nghiệm, chỉ rõ cho học sinh cách dùng dấu ); (; [;].

3A. Viết bằng kí hiệu tập hợp và biểu diễn tập nghiệm các bất phương trình sau trên trục số:

a) $x>4;$                 b) $x<-5;$               c) $x\ge 7;$                  d)  $x\le \frac{3}{4}$.

3B. Viết bằng kí hiệu tập hợp và biểu diễn tập nghiệm các bất phương trình sau trên trục số.

a) $x\le -3;$               b) $x<\frac{7}{5};$                c) $x\ge -9;$               d) $x>5.$.

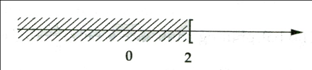
4A. Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào?

a) 

b)