Ta có:

+ 5 - x < 1 ⇔ 4 < x

+ 3x + 1 < 4 ⇔ 3x < 3 ⇔ x > 1

+ 4x - 11 > x ⇔ 3x > 11 ⇔ x > $\frac{11}{3}$

+ 2x - 1 > 3 ⇔ 2x > 4 ⇔ x > 2

Vậy x = 3 là nghiệm của bất phương trình 2x - 1 > 3

Chọn đáp án D.

Tập nghiệm của bất phương trình: x ≤ 2 là S = { x| x ≤ 2 }.

Chọn đáp án B.

Ta có:

+ 2x - 4 < 0 ⇔ x < 2

+ 2x - 4 > 0 ⇔ x > 2

+ 2x - 4 ≤ 0 ⇔ x ≤ 2

+ 2x - 4 ≥ 0 ⇔ x ≥ 2

Chọn đáp án B.

Ta có: 3x - 6 > 0 ⇔ 3x > 6 ⇔ x > 2

Vậy bất phương trình x > 2 tương đương với bất phương trình đã cho.

Chọn đáp án C.

   * Thay x = 2 vào bất phương trình x + 2 > 4 ta được: 2 + 2 > 4 là khẳng định sai nên x = 2 không là nghiệm của bất phương trình.

   * Thay x = 2 vào bất phương trình 4 -2x < 4 ta được: 4 – 2.2 < 4 là khẳng định đúng nên x = 2 là nghiệm của bất phương trình.

   * Thay x = 2 vào bất phương trình 4x - 2 < 2 ta được: 4.2 - 2 < 2 là khẳng định sai nên x = 2 không là nghiệm của bất phương trình.

   * Thay x = 2 vào bất phương trình x -10 > 2 ta được: 2 - 10 > 2 là khẳng định sai nên x = 2 không là nghiệm của bất phương trình.

Chọn đáp án B

Trong hình vẽ trên tất cả các điểm bên trái điểm 3 bị gạch bỏ nên hình vẽ đã cho biểu diễn tập nghiệm {x | x ≥ 3}

Chọn đáp án D

Trong hình vẽ trên các điểm bên phải điểm 4 và số 4 bị gạch nên hình vẽ biểu diễn tập nghiệm: {x | x < 4}

Chọn đáp án A

Các điểm bên phải điểm -2 bị gạch nên hình vẽ trên biểu diễn tập nghiệm : {x | x ≤ -2}

Chọn đáp án C

Gọi số kẹo mỗi bạn nhận được là x ( cái kẹo)

Khi đó, 4 bạn sẽ có tất cả: 4x ( cái kẹo)

Để sau khi chia xong, cô Lan vẫn còn kẹo thì 4x < 20

Chọn đáp án A

Giá của x quyển vở là: 3000.x đồng

Tổng số tiền mua 1 cái bút và x quyển vở là: 8000 + 3 000x (đồng)

Vì số tiền bạn Huyền có là 30000 đồng nên ta có:

Chọn đáp án B

Bài 11: Biểu diễn tập nghiệm của bất phương trình x ≥ 8 trên trục số, ta được?

Lời giải:

Ta biểu diễn x ≥ 8 trên trục số như sau:

Chọn đáp án C

Bài 12: Biểu diễn tập nghiệm của bất phương trình x > 8 trên trục số, ta được?

Lời giải:

Ta biểu diễn x > 8 trên trục số như sau:

Chọn đáp án D

Bài 13: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? Hãy chọn câu đúng?

Lời giải:

Bất phương trình dạng ax + b > 0 (hoặc ax + b < 0, ax + b ≥ 0, ax + b ≤ 0) trong đó a và b là hai số đã cho, a ≠ 0, gọi là bất phương trình bậc nhất một ẩn.

Nên y < 10 - 2y là bất phương trình bậc nhất một ẩn.

Chọn đáp án B

II. Bài tập tự luận có giải

Lời giải

1 - 3x ≥ 2 - x

⇔ 1 - 3x + x - 2 ≥ 0

⇔ -2x - 1 ≥ 0

⇔ -2x - 1

⇔ x ≤ - 

Vậy nghiệm của bất phương trình S = 

Lời giải

Vậy bất phương trình có nghiệm x ≥ -.

Lời giải

+ Thay x = -3 vào bất phương trình 2x + 1 > 5 ta được

2. (-3) + 1 > 5 ⇔ -5 > 5 (vô lý) nên x = -3 không là nghiệm của bất phương trình 2x + 1 > 5.

+ Thay x = -3 vào bất phương trình 7 - 2x < 10 - x ta được

7 - 2. (-3) < 10 - (-3) ⇔ 13 < 13 (vô lý) nên x = -3 không là nghiệm của bất phương trình 7 - 2x < 10 - x.

+ Thay x = -3 vào bất phương trình 2 + x < 2 + 2x ta được

2 + (-3) < 2 + 2. (-3) ⇔ -1 < -4 (vô lý) nên x = -3 không là nghiệm của bất phương trình 2 + x < 2 + 2x.

+ Thay x = -3 vào bất phương trình -3x > 4x + 3 ta được

-3. (-3) > 4. (-3) + 3 ⇔ 9 > -9 (luôn đúng) nên x = -3 là nghiệm của bất phương trình -3x > 4x + 3.

Lời giải

Thay x = -3 vào từng bất phương trình ta được:

Đáp án A: 2. (-3) + 1 = -5 > -5 (vô lí) nên x = -3 không là nghiệm của bất phương trình.

Đáp án B: VT = 7 - 2. (-3) = 14, Vp = 10 - (-3) = 13 nên 13 ≤ 13 (đúng) nên x = -3 là nghiệm của bất phương trình.

Đáp án C: VT = 3. (-3) - 2 = -11, VP = 6 - 2. (-3) = 12 nên -11 ≤ 12 (đúng) nên x = -3 là nghiệm của bất phương trình.

Đáp án D: VT = -3. (-3) = 9, VP = 4. (-3) + 3 = -9 nên 9 > -9 (đúng) nên x = -3 là nghiệm của bất phương trình.

Lời giải

Giải từng bất phương trình ta được

+) 2(x - 1) < x ⇔ 2x - 2 < x ⇔ 2x - x < 2 ⇔ x < 2

+) 2(x - 1) ≤ x - 4 ⇔ 2x - 2 ≤ x - 4 ⇔ 2x - x < -4 + 2 ⇔ x ≤ -2

+) 2x < x - 4 ⇔ 2x - x < -4 ⇔ x < -4

+) 2(x - 1) < x - 4 ⇔ 2x - 2 < x - 4 ⇔ 2x - x < -4 + 2 ⇔ x < -2

* Hình vẽ biểu diễn tập nghiệm S = {x < -2}.

Nên bất phương trình 2(x - 1) < x - 4 thỏa mãn.

Bài 6 Mỗi khẳng định sau đúng hay sai? Vì sao

a) (-6).5 < (-5).5 ;

b) (-6).(-3) < (-5).(-3);

c) (-2003).(-2005) ≤ (-2005).2004;

d) -3x²≤ 0.

Lời giải:

a) Ta có: -6 < -5

⇒ (-6).5 < (-5).5 (Nhân cả hai vế với 5 > 0 được BĐT cùng chiều).

⇒ Khẳng định a) đúng.

b) -6 < -5

⇒ (-6).(-3) > (-5).(-3) (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).

⇒ Khẳng định b) sai.

c) -2003 < 2004

⇒ (-2003).(-2005) > (-2005).2004 (Nhân cả hai vế với -2005 < 0, BĐT đổi chiều)

⇒ Khẳng định c) sai.

d) x²≥ 0 với mọi x ∈

⇒ (-3).x² ≤ (-3).0 (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).

hay -3x² ≤ 0.

⇒ Khẳng định d) đúng với mọi số thực x.

Bài 7 Cho a < b, hãy so sánh:

2a và 2b; 2a và a + b; -a + b; -a và -b.

Lời giải:

+ a < b ⇒ 2a < 2b (nhân cả 2 vế với 2 > 0, BĐT không đổi chiều).

+ a < b ⇒ a + a < b + a (Cộng cả 2 vế với a)

hay 2a < a + b.

+ a < b ⇒ (-1).a > (-1).b (Nhân cả 2 vế với -1 < 0, BĐT đổi chiều).

hay –a < -b.

Bài 8 Số a là số âm hay dương nếu:

12a < 15 a ?     4a < 3a ?     -3a > -5a?

Lời giải:

a) Ta có: 12 < 15 (*). Để có bất đẳng thức cùng chiều là 12a < 15a ta phải nhân cả 2 vế của (*) với số dương. Vậy a là số dương.

b) Ta có: 4 > 3 (**). Để có bất đẳng thức trái chiều là 4a < 3a ta phải nhân cả 2 vế của (**) với số âm. Vậy a là số âm.

c) Ta có: -3 > -5 (***). Để có bất đẳng thức cùng chiều là -3a > -5a ta phải nhân cả 2 vế của (*) với số dương. Vậy a là số dương.

Bài 9 Cho a < b, chứng tỏ:

a) 2a - 3 < 2b - 3;     b) 2a - 3 < 2b + 5.

Lời giải:

a) Ta có: a < b

⇒ 2a < 2b (Nhân cả hai vế với 2 > 0, BĐT không đổi chiều).

⇒ 2a – 3 < 2b – 3 (Cộng cả hai vế với -3, BĐT không đổi chiều).

Vậy 2a – 3 < 2b – 3.

b) Ta có: -3 < 5

⇒ 2b - 3 < 2b + 5 (cộng vào 2 vế với 2b)

mà 2a - 3 < 2b - 3 (chứng minh ở câu a))

Vậy: 2a - 3 < 2b + 5 (Tính chất bắc cầu).

Bài 10

a) Nhân cả hai vế của bất đẳng thức -2 < 3 với 5091 thì được bất đẳng thức nào ?

b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức nào ?

a) - 2. 5091 = - 10 182 và 3. 5091 = 15 273

⇒ - 10 182 < 15 273

b) Nhân cả 2 vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức: -2c < 3c

III. Bài tập vận dụng

Bài 1

a) Hãy cho biết vế trái, vế phải của bất phương trình x² ≤ 6x –5

b) Chứng tỏ các số 3; 4 và 5 đều là nghiệm, còn số 6 không phải là nghiệm của bất phương trình vừa nêu.

Bài 2 Hãy cho biết vế trái, vế phải và tập nghiệm của bất phương trình x > 3, bất phương trình 3 < x và phương trình x = 3.

Bài 3 Viết và biểu diễn tập nghiệm của bất phương trình x ≥ -2 trên trục số.

Bài 4 Viết và biểu diễn tập nghiệm của bất phương trình x < 4 trên trục số.

Bài 5 Kiểm tra xem giá trị x = 3 là nghiệm của bất phương trình nào trong các bất phương trình sau:

a) 2x + 3 < 9

b) -4x > 2x + 5

c) 5 - x > 3x - 12

Bài 6 Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:

a) x < 4 ; b) x ≤ -2

c) x > -3 ; d) x ≥ 1

Bài 7 Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).

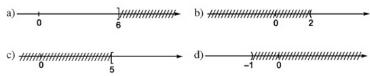
Bài 8 Hãy lập bất phương trình cho bài toán sau:

Bài 9 Quãng đường từ A đến B dài 50km. Một ô tô đi từ A đến B, khởi hành lúc 7h. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước 9 giờ cùng ngày?

Bài 10 Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:

a) $x<4$

b) $x\le -2$

c) $x>-3$

d) $x\ge 1$

Bài 11 Hãy lập bất phương trình cho bài toán sau:

Quãng đường đi từ A đến B dài 50km. Một ô tô đi từ A đến B, khởi hành lúc 7 giờ. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước 9 giờ cùng ngày?

B. Lý thuyết Bất phương trình một ẩn

1. Bất phương trình một ẩn

Bất phương trình một ẩn x là bất phương trình có dạng:

$A\left(x\right)<B\left(x\right)$ hoặc  $A\left(x\right)>B\left(x\right)$

hoặc $A\left(x\right)\le B\left(x\right)$ hoặc  $A\left(x\right)\ge B\left(x\right)$

Trong đó A(x) là vế trái và B(x) là vế phải.

Ví dụ: $2x^2-5x+3\ge 0$ là một bất phương trình ẩn x

$\frac{1}{2}t-4<2t+3$ là một bất phương trình bậc nhất ẩn t.

2. Nghiệm của bất phương trình một ẩn

Giá trị x₀ được gọi là nghiệm của bất phương trình A(x) < B(x) nếu bất đẳng thức A(x₀) < B(x₀) đúng.

Tương tự đối với các dạng bất phương trình còn lại.

3. Giải bất phương trình một ẩn

Giải bất phương trình là đi tìm tập nghiệm  của bất phương trình đó.

4. Hai bất phương trình tương đương

Hai bất phương trình gọi là tương đương nếu chúng có cùng tập nghiệm

Chú ý: hai bất phương trình cùng vô nghiệm tương đương nhau.