Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 6: Trường hợp đồng dạng thứ hai hay, chi tiết giúp học sinh dễ dàng làm bài tập Trường hợp đồng dạng thứ hai lớp 8.

Giải bài tập Toán lớp 8 Bài 6: Trường hợp đồng dạng thứ hai

Trả lời câu hỏi giữa bài

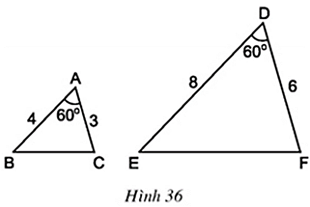
Câu hỏi 1 trang 75 Toán 8 Tập 2: Cho hai tam giác ABC và DEF có kích thước như trong hình 36.

- So sánh các tỉ số $\frac{AB}{DE};\frac{AC}{DF}$ .

- Đo các đoạn thẳng BC, EF. Tính tỉ số  $\frac{BC}{EF}$, so sánh với các tỉ số trên và dự đoán sự đồng dạng của hai tam giác ABC và DEF.

Lời giải:

Ta có:

$$\begin{gathered} \frac{AB}{DE}=\frac{4}{8}=\frac{1}{2}; \\ \frac{AC}{DF}=\frac{3}{6}=\frac{1}{2} \\ \Rightarrow \frac{AB}{DE}=\frac{AC}{DF}=\frac{1}{2} \end{gathered}$$

Đo các cạnh ta có: BC = 3,6 cm; EF = 7,2 cm

Suy ra: $\frac{BC}{EF}=\frac{1}{2}$.

Vậy

 $\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{1}{2}$

Dự đoán : ΔABC $~$ ΔDEF.

Câu hỏi 2 trang 76 Toán 8 Tập 2: Hãy chỉ ra các cặp tam giác đồng dạng với nhau từ các tam giác sau đây (h.38):

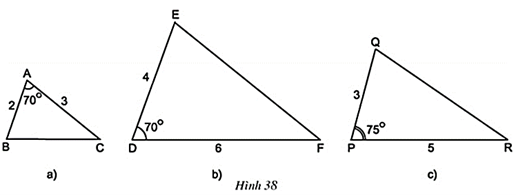
Lời giải:

Xét ΔABC và ΔDEF có

$\widehat{A}=\widehat{D}$ = 70^o

$\frac{AB}{DE}=\frac{AC}{DF}\left(=\frac{1}{2}\right)$

⇒ ΔABC $~$ ΔDEF (c.g.c)

Câu hỏi 3 trang 77 Toán 8 Tập 2: a) Vẽ tam giác ABC có $\widehat{BAC}$= 50^o, AB = 5cm, AC = 7,5cm (h.39)

b) Lấy trên các cạnh AB, AC lần lượt hai điểm D, E sao cho AD = 3cm, AE = 2cm. Hai tam giác AED và ABC có đồng dạng với nhau không ? Vì sao ?

Lời giải:

a)

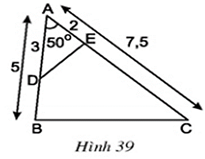
b) Ta có:

 $\frac{AD}{AC}=\frac{3}{7,5}=\frac{2}{5}$

Xét tam giác AED và ABC có:

$\widehat{A}$chung

$\frac{AD}{AC}=\frac{AE}{AB}\left(=\frac{2}{5}\right)$

Suy ra: ∆AED  $~$ ∆ABC ( c.g.c).

Bài tập (trang 77)

Bài 32 trang 77 Toán 8 Tập 2: Trên một cạnh của góc xOy ( $\widehat{xOy}$≠ 180^o), đặt các đoạn thẳng OA = 5cm, OB = 16cm. Trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC = 8cm, OD = 10cm.

a) Chứng minh hai tam giác OCB và OAD đồng dạng.

b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có các góc bằng nhau từng đôi một.

Lời giải:

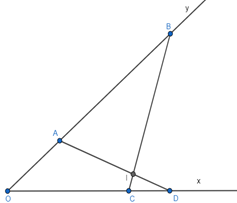
a) Ta có:

$$\begin{gathered} \frac{OA}{OC}=\frac{5}{8};\frac{OD}{OB}=\frac{10}{16}=\frac{5}{8} \\ \Rightarrow \frac{OA}{OC}=\frac{OD}{OB} \end{gathered}$$

Xét ∆OCB và ∆OAD có:

 $\widehat{O}$chung

$\frac{OA}{OC}=\frac{OD}{OB}$

Suy ra: ∆OCB $~$ ∆OAD (c – g – c).

b) Xét ∆ICD  và ∆IAB có:

$\widehat{CID}=\widehat{AIB}$( đối đỉnh)

$\widehat{CDI}=\widehat{IBA}$ (hai góc tương ứng của hai tam giác đồng dạng ∆OCB ∆OAD).

$\Rightarrow \widehat{BAI}=\widehat{ICD}$ (tính chất tổng ba góc trong một tam giác)

Vậy hai tam giác ICD và IAB có các góc bằng nhau từng đôi một.

Bài 33 trang 77 Toán 8 Tập 2: Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k, thì tỉ số của hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.

Lời giải:

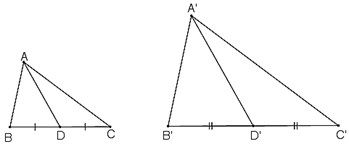
Giả sử ΔA’B’C’ $~$  ΔABC theo tỉ số k.

Suy ra: 

$\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}C\text{'}}{BC}=k;\widehat{B}=\widehat{B\text{'}}$

Gọi D, D’ lần lượt là trung điểm BC và B’C’.

Ta có:

 $$\begin{gathered} \frac{A\text{'}B\text{'}}{AB}=k; \\ \frac{B\text{'}D\text{'}}{BD}=\frac{2B\text{'}D\text{'}}{2BD} \\ =\frac{B\text{'}C\text{'}}{BC}=k \end{gathered}$$

Suy ra: $\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}D\text{'}}{BD}$.

Xét ∆A’B’D’ và ∆ ABD có:

$\widehat{B\text{'}}=\widehat{B}$

$\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}D\text{'}}{BD}$ ( chứng minh trên).

⇒ ΔA’B’D’ $~$  ∆ABD (c – g – c) theo tỉ số k.

Suy ra: $\frac{A\text{'}D\text{'}}{AD}=k$  ( đpcm).

Bài 34 trang 77 Toán 8 Tập 2: Dựng tam giác ABC, biết  $\widehat{A}$= 60º; tỉ số  $\frac{AB}{AC}=\frac{4}{5}$ và đường cao AH = 6cm

Lời giải:

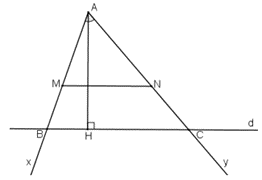
* Cách dựng:

+ Dựng góc $\widehat{xAy}={60}^0$

+ Trên tia Ax lấy điểm M sao cho AM = 4; trên tia Ay lấy điểm N sao cho AN = 5.

+ Kẻ tia At vuông góc với MN

+ Trên tia At lấy điểm H sao cho AH = 6cm.

+ Kẻ đường thẳng d qua H và vuông góc với At cắt Ax và Ay lần lượt tại B và C.

Ta được tam giác ABC cần dựng.

* Chứng minh :

ΔABC dựng được có AH ⊥ BC ; AH = 6 và  $\widehat{A}$= 60º;

Lại có AH ⊥ BC, MN ⊥ AH ⇒ MN // BC

⇒ ΔAMN  $~$ ΔABC

Suy ra: $\frac{AM}{AB}=\frac{AN}{AC}$.

Suy ra: $\frac{AB}{AC}=\frac{AM}{AN}=\frac{4}{5}$

Vậy tam giác ABC dựng được thỏa mãn yêu cầu đề bài.