Với giải Hoạt động khám phá 1 trang 21 Toán 12 Tập 2 Chân trời sáng tạo chi tiết trong Bài 3: Ứng dụng hình học của tích phân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 3: Ứng dụng hình học của tích phân

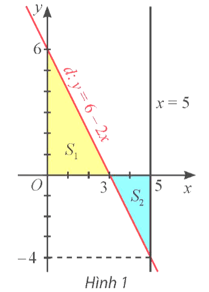
Hoạt động khám phá 1 trang 21 Toán 12 Tập 2: Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S₁ là diện tích hình phẳng giới hạn bởi d, trục hoành và trục tung, S₂ là diện tích hình phẳng giới hạn bởi d, trục hoành và đường thẳng x = 5 (Hình 1).

a) Tính S₁ và so sánh với $\underset{0}{\overset{3}{\int }}f\left(x\right)dx$.

b) Tính S₂ và so sánh với $\underset{3}{\overset{5}{\int }}f\left(x\right)dx$.

c) So sánh $\underset{0}{\overset{5}{\int }}\left|f\left(x\right)\right|dx$ với S₁ + S₂.

Lời giải:

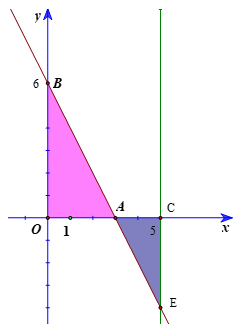
a) Gọi A(3; 0), B(0; 6), C(5; 0), E(5; −4).

Ta có S₁ chính là diện tích của tam giác vuông OAB với OA = 3, OB = 6.

Do đó $S_1=S_{\Delta OAB}=\frac{1}{2}OA.OB=\frac{1}{2}\mathrm{.3.6}=9$.

Ta có $\underset{0}{\overset{3}{\int }}f\left(x\right)dx=\underset{0}{\overset{3}{\int }}\left(6-2x\right)dx$ $={\left.\left(6x-x^2\right)\right|}_0^3$= 9.

Vậy $S_1=\underset{0}{\overset{3}{\int }}f\left(x\right)dx$.

b) Ta có S₂ chính là diện tích của tam giác vuông ACE với AC = 2, CE = 4.

Do đó $S_2=S_{\Delta ACE}=\frac{1}{2}AC.CE=\frac{1}{2}\mathrm{.2.4}=4$.

Ta có $\underset{3}{\overset{5}{\int }}f\left(x\right)dx=\underset{3}{\overset{5}{\int }}\left(6-2x\right)dx$$={\left.\left(6x-x^2\right)\right|}_3^5$= 5 – 9 = −4.

Do đó $S_2=-\underset{3}{\overset{5}{\int }}f\left(x\right)dx$.

c) Ta có $\underset{0}{\overset{5}{\int }}\left|f\left(x\right)\right|dx\underset{0}{\overset{5}{\int }}\left|6-2x\right|dx$$=\underset{0}{\overset{3}{\int }}\left|6-2x\right|dx+\underset{3}{\overset{5}{\int }}\left|6-2x\right|dx$

$=\underset{0}{\overset{3}{\int }}\left(6-2x\right)dx+\underset{3}{\overset{5}{\int }}\left(2x-6\right)dx$$={\left.{\left.\left(6x-x^2\right)\right|}_0^3+\left(x^2-6x\right)\right|}_3^5$

= 9 − 5 + 9 = 13.

Có S₁ + S₂ = 9 + 4 = 13 = $\underset{0}{\overset{5}{\int }}\left|f\left(x\right)\right|dx$.