Với tóm tắt lý thuyết Toán lớp 12 Bài 10: Phương sai và độ lệch chuẩn sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán 12 Bài 10: Phương sai và độ lệch chuẩn

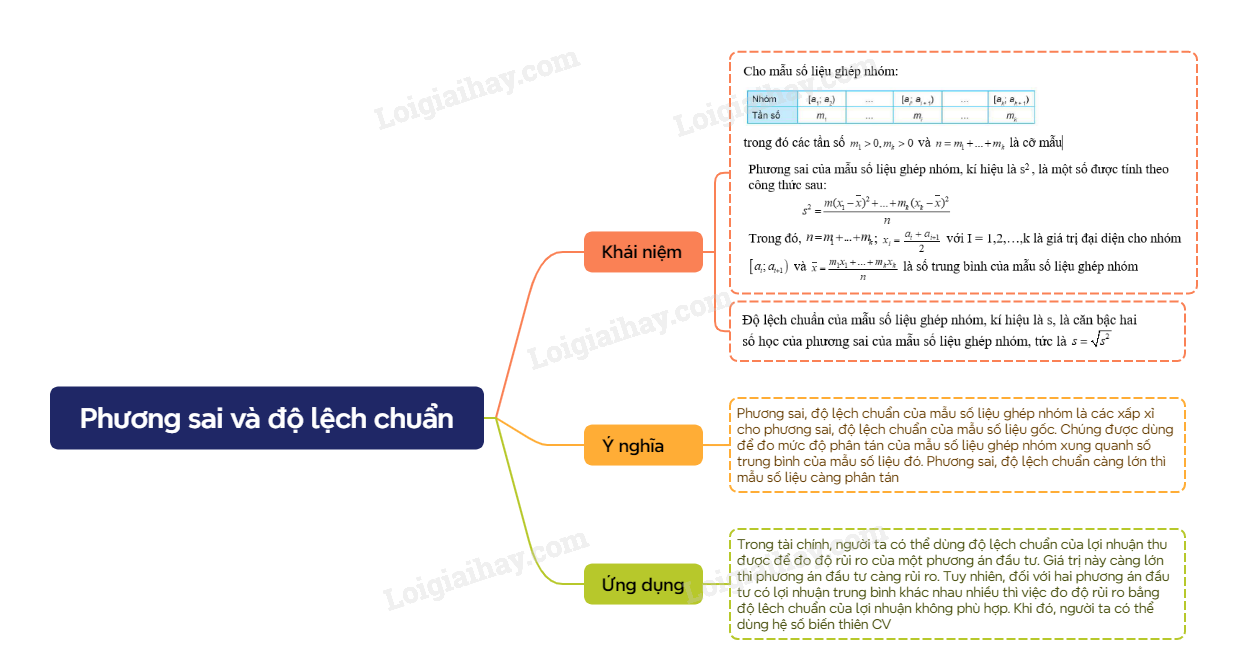
A. Lý thuyết Phương sai và độ lệch chuẩn

1. Phương sai và độ lệch chuẩn

Cho mẫu số liệu ghép nhóm:

trong đó các tần số $m_1>0,m_k>0$ và $n=m_1+...+m_k$ là cỡ mẫu

Ý nghĩa: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán

2. Sử dụng phương sai, độ lệch chuẩn đo độ rủi ro

Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?

Giải:

Chọn giá trị đại diện cho các nhóm số liệu ta có:

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:

$\overline{x_A}=\frac{1}{60}(5.7,5+...+5.27,5)=17,5$ (triệu đồng)

$\overline{x_B}=\frac{1}{60}(20.7,5+...+20.27,5)=17,5$ (triệu đồng)

Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau

Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:

$s_A=\sqrt{\frac{1}{60}(5.7,5^2+...+5.27,5^2-17,5^2}=5$

$s_B=\sqrt{\frac{1}{60}(20.7,5^2+...+20.27,5^2-17,5^2}\approx 8,42$

Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn

Sơ đồ tư duy Phương sai và độ lệch chuẩn

B. Bài tập Phương sai và độ lệch chuẩn

Bài 1. Phương sai của mẫu số liệu ghép nhóm, được tính bởi công thức:

A. $s=\frac{1}{n}\left(m_1{x}_1^2+m_2{x}_2^2+\mathrm{...}+m_k{x}_k^2\right)$.

B. $s=\frac{1}{n}\left(m_1{x}_1^2+m_2{x}_2^2+\mathrm{...}+m_k{x}_k^2\right)-{\overline{x}}^2$.

C. $s^2=\frac{1}{n}\left(m_1{x}_1^2+m_2{x}_2^2+\mathrm{...}+m_k{x}_k^2\right)-{\overline{x}}^2$.

D. $s^2=\frac{1}{n}\left(m_1{x}_1^2+m_2{x}_2^2+\mathrm{...}+m_k{x}_k^2\right)$.

Hướng dẫn giải

Đáp án đúng là: C

Phương sai của mẫu số liệu ghép nhóm, được tính bởi công thức:

$s^2=\frac{1}{n}\left(m_1{x}_1^2+m_2{x}_2^2+\mathrm{...}+m_k{x}_k^2\right)-{\overline{x}}^2$.

Bài 2. Độ lệch chuẩn của mẫu số liệu ghép nhóm được tính bằng:

A. Căn bậc hai số học của phương sai.

B. Một nửa căn bậc hai số học của phương sai.

C. Căn bậc ba của phương sai.

D. Căn bậc hai số học của phương sai trừ 1.

Hướng dẫn giải

Đáp án đúng là: A

Độ lệch chuẩn của mẫu số liệu ghép nhóm được tính bằng căn bậc hai số học của phương sai.

Bài 3. An tìm hiểu hàm lượng chất béo (đơn vị: g) có trong 100 g mỗi loại thực phẩm. Sau khi thu thập dữ liệu về 60 loại thực phẩm, An lập được bảng thống kê

Tìm phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Ta có bảng thống kê hàm lượng chất béo theo giá trị đại diện

Giá trị trung bình là:

$\overline{x}=\frac{2.4+6.8+10.12+13.16+16.20+13.24}{60}\approx 16,9$.

Phương sai của mẫu số liệu là

$s^2=\frac{{2.4}^2+{6.8}^2+{10.12}^2+{13.16}^2+{16.20}^2+{13.24}^2}{60}-{\left(16,9\right)}^2\approx 32,25$.

Độ lệch chuẩn của mẫu số liệu là

$s=\sqrt{32,25}\approx 5,68$.

Bài 4. Khảo sát cân nặng của 30 bạn học sinh (đơn vị: kilogam), ta có mẫu số liệu sau

Xác định cân nặng trung bình, độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Ta có mẫu số liệu theo giá trị đại diện như sau

Cân nặng trung bình là

$\overline{x}=\frac{1.17,5+1.32,5+10.37,5+17.42,5+1.52,5}{30}=40$.

Phương sai của mẫu số liệu là

$s^2=\frac{1.17,5^2+1.32,5^2+10.37,5^2+17.42,5^2+1.52,5^2}{30}-{40}^2\approx 29,58$.

Độ lệch chuẩn của mẫu số liệu là

$s=\sqrt{29,58}\approx 5,44$.

Bài 5. Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng A và B được cho ở bảng sau:

Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên và so sánh cân nặng cam ở lô hàng nào đồng đều hơn?

Hướng dẫn giải

Ta có mẫu số liệu số lượng cam theo giá trị đại diện

Xét lô hàng A.

Cân nặng trung bình của mỗi quả là

$\overline{x_1}=\frac{2.152,5+6.157,5+12.162,5+4.167,5+1.172,5}{25}=161,7$.

Phương sai của mẫu số liệu là

$s_1^2=\frac{2.152,5^2+6.157,5^2+12.162,5^2+4.167,5^2+1.172,5^2}{25}-{\left(161,7\right)}^2=21,36$.

Độ lệch chuẩn của mẫu số liệu là

$s_1=\sqrt{21,36}\approx 4,62$.

Xét lô hàng B.

Cân nặng trung bình của mỗi quả là

$\overline{x_2}=\frac{1.152,5+3.157,5+7.162,5+10.167,5+4.172,5}{25}=165,1$.

Phương sai của mẫu số liệu là

$s_2^2=\frac{1.152,5^2+3.157,5^2+7.162,5^2+10.167,5^2+4.172,5^2}{25}-{\left(165,1\right)}^2=26,24$.

Độ lệch chuẩn của mẫu số liệu là

$s_2=\sqrt{26,24}\approx 5,12$.

Dựa vào phương sai và độ lệch chuẩn ta thấy lô hàng A khối lượng các quả cam đồng đều hơn.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Kết nối tri thức hay, chi tiết khác: