Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 10: Phương sai và độ lệch chuẩn chi tiết sách Toán 12 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 10: Phương sai và độ lệch chuẩn

Mở đầu trang 80 Toán 12 Tập 1: Để xác định độ ổn định của một máy đo độ ẩm không khí, người ta dùng máy này để đo 20 lần. Nếu độ lệch chuẩn của mẫu số liệu đo lớn hơn 0,15 thì người ta sẽ đưa máy đo đi sửa chữa. Trong một lần lấy mẫu, kĩ thuật viên có được mẫu số liệu ghép nhóm như sau:

Liệu có cần đưa máy đo này đi sửa chữa hay không?

Lời giải:

Sau khi học xong bài này, ta giải quyết bài toán này như sau:

Chọn giá trị đại diện cho mẫu số liệu ta có:z

Độ ẩm trung bình là: $\frac{\mathrm{52,05.1}+\mathrm{52,15.5}+\mathrm{52,25.8}+\mathrm{52,35.4}+\mathrm{52,45.2}}{20}=\mathrm{52,255}$ .

Phương sai:

$s^2=\frac{{\mathrm{52,05}}^2.1+{\mathrm{52,15}}^2.5+{\mathrm{52,25}}^2.8+{\mathrm{52,35}}^2.4+{\mathrm{52,45}}^2.2}{20}-{\mathrm{52,255}}^2=\mathrm{0,010475}$.

Độ lệch chuẩn là: $s=\sqrt{\mathrm{0,010475}}\approx \mathrm{0,102}$.

Vì s = 0,102 < 0,15 do đó không cần đưa máy đo này đi sửa chữa.

1. Phương sai và độ lệch chuẩn

HĐ1 trang 80 Toán 12 Tập 1: Trở lại bài toán trong tình huống mở đầu. Gọi x1, …, x¬20 là các kết quả đo (mẫu số liệu gốc).

a) Có thể tính được chính xác phương sai và độ lệch chuẩn của mẫu số liệu gốc hay không?

b) Thảo luận và đề xuất ước lượng cho phương sai và độ lệch chuẩn của mẫu số liệu gốc.

Lời giải:

Gọi x₁, …, x­₂₀ là các kết quả đo (mẫu số liệu gốc).

a) Ta không thể tính chính xác được phương sai và độ lệch chuẩn của mẫu số liệu gốc.

b) Gọi x₁; x₂; x₃; x₄; x₅ lần lượt là giá trị đại diện của 5 nhóm [52; 52,1), [52,1; 52,2), [52,2; 52,3), [52,3; 52,4), [52,4; 52,5).

Gọi số trung bình của mẫu số liệu.

Phương sai: $s^2=\frac{{\left(x_1-\overline{x}\right)}^2+5{\left(x_2-\overline{x}\right)}^2+8{\left(x_3-\overline{x}\right)}^2+4{\left(x_4-\overline{x}\right)}^2+2{\left(x_5-\overline{x}\right)}^2}{20}$ .

Độ lệch chuẩn $s=\sqrt{s^2}$.

Luyện tập 1 trang 82 Toán 12 Tập 1: Một vận động viên luyện tập chạy cự li 100 m đã ghi lại kết quả luyện tập như sau:

Tìm phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm này. Phương sai và độ lệch chuẩn cho biết điều gì?

Lời giải:

Chọn giá trị đại diện cho mẫu số liệu ta có:

Tổng số vận động viên là: 3 + 7 + 8 + 2 = 20.

Thời gian chạy trung bình là: $\frac{\mathrm{10,3.3}+\mathrm{10,5.7}+\mathrm{10,7.8}+\mathrm{10,9.2}}{20}=\mathrm{10,59}$ .

Phương sai của mẫu số liệu là

$s^2=\frac{{\mathrm{10,3}}^2.3+{\mathrm{10,5}}^2.7+{\mathrm{10,7}}^2.8+{\mathrm{10,9}}^2.2}{20}-{\mathrm{10,59}}^2=\mathrm{0,0299}$.

Độ lệch chuẩn của mẫu số liệu là: $s=\sqrt{\mathrm{0,0299}}\approx \mathrm{0,17}$.

Dựa vào phương sai và độ lệch chuẩn ta có kết luận rằng mẫu số liệu kết quả luyện tập có tính đồng đều, dữ liệu có xu hướng gần giá trị trung bình và ít bị phân tán.

Vận dụng trang 82 Toán 12 Tập 1: Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm cho bài toán trong tình huống mở đầu và cho biết có cần đưa máy đi sửa chữa hay không?

Lời giải:

Chọn giá trị đại diện cho mẫu số liệu ta có:

Độ ẩm trung bình là: $\frac{\mathrm{52,05.1}+\mathrm{52,15.5}+\mathrm{52,25.8}+\mathrm{52,35.4}+\mathrm{52,45.2}}{20}=\mathrm{52,255}$.

Phương sai:

$s^2=\frac{{\mathrm{52,05}}^2.1+{\mathrm{52,15}}^2.5+{\mathrm{52,25}}^2.8+{\mathrm{52,35}}^2.4+{\mathrm{52,45}}^2.2}{20}-{\mathrm{52,255}}^2=\mathrm{0,010475}$.

Độ lệch chuẩn là: $s=\sqrt{\mathrm{0,010475}}\approx \mathrm{0,102}$ .

Vì s = 0,102 < 0,15 do đó không cần đưa máy đo này đi sửa chữa.

Bài tập

Bài 3.4 trang 84 Toán 12 Tập 1: Kiểm tra khối lượng của 30 bao xi măng (đơn vị: kg) được chọn ngẫu nhiên trước khi xuất xưởng cho kết quả như sau:

a) Thay dấu “?” bằng số thích hợp để hoàn thiện mẫu số liệu ghép nhóm sau.

b) Tính phương sai và độ lệch chuẩn của mẫu số liệu gốc và mẫu số liệu ghép nhóm. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?

Lời giải:

a) Chọn giá trị đại diện cho mẫu số liệu ta có:

b) Mẫu số liệu gốc

Giá trị trung bình là:

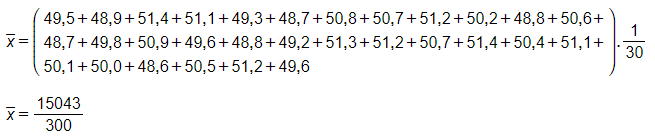
Phương sai

Ta có bảng sau

Tổng bình phương độ lệch là: $\frac{78461}{3000}$.

Khi đó phương sai: $s^2=\frac{78461}{3000}.\frac{1}{30}=\frac{78461}{90000}$ .

Độ lệch chuẩn là $s=\sqrt{\frac{78461}{90000}}\approx \mathrm{0,934}$.

Mẫu số liệu ghép nhóm

Chọn giá trị đại diện cho mẫu số liệu ta có:

Giá trị trung bình là:

$\overline{x}=\frac{\mathrm{48,75.6}+\mathrm{49,25.2}+\mathrm{49,75.4}+\mathrm{50,25.4}+\mathrm{50,75.6}+\mathrm{51,25.8}}{30}=\frac{3011}{60}$.

Phương sai:

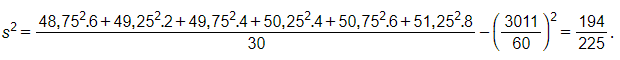
Độ lệch chuẩn: $s=\sqrt{\frac{194}{225}}\approx \mathrm{0,929}$ .

Giá trị mẫu số liệu gốc là chính xác, giá trị mẫu số liệu ghép nhóm là xấp xỉ.

Bài 3.5 trang 84 Toán 12 Tập 1: Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản cuất bởi hai phân xưởng được cho như sau:

Tìm phương sai và độ lệch chuẩn của mỗi mẫu số liệu ghép nhóm và nhận xét về độ phân tán của tuổi thọ các linh kiện điện tử được sản xuất bởi mỗi phân xưởng.

Lời giải:

Chọn giá trị đại diện cho mẫu số liệu ta có:

Tuổi thọ trung bình của các linh kiện của phân xưởng 1 là:

$\overline{x_1}=\frac{\mathrm{4.1,75}+\mathrm{9.2,25}+\mathrm{13.2,75}+\mathrm{8.3,25}+\mathrm{6.3,75}}{4+9+13+8+6}=\mathrm{2,7875}$.

Tuổi thọ trung bình của các linh kiện của phân xưởng 2 là:

$\overline{x_2}=\frac{\mathrm{2.1,75}+\mathrm{8.2,25}+\mathrm{20.2,75}+\mathrm{7.3,25}+\mathrm{3.3,75}}{2+8+20+7+3}=\mathrm{2,7625}$.

Phương sai và độ lệch chuẩn của các linh kiện của phân xưởng 1 là:

Suy ra $s_1^2=\frac{{\mathrm{4.1,75}}^2+{\mathrm{9.2,25}}^2+{\mathrm{13.2,75}}^2+{\mathrm{8.3,25}}^2+{\mathrm{6.3,75}}^2}{40}-{\left(\mathrm{2,7875}\right)}^2\approx \mathrm{0,355}$ .

Phương sai và độ lệch chuẩn của các linh kiện của phân xưởng 2 là:

$s_2^2=\frac{{\mathrm{2.1,75}}^2+{\mathrm{8.2,25}}^2+{\mathrm{20.2,75}}^2+{\mathrm{7.3,25}}^2+{\mathrm{3.3,75}}^2}{40}-{\left(\mathrm{2,7625}\right)}^2\approx \mathrm{0,219}$.

Suy ra $s_2=\sqrt{\mathrm{0,219}}\approx \mathrm{0,47}$ .

Đối với mẫu số liệu này thì phương sai và độ lệch chuẩn nhỏ nên độ phân tán của số liệu thấp. Do đó các giá trị của mẫu số liệu tập trung quanh giá trị trung bình.

Bài 3.6 trang 84 Toán 12 Tập 1: Một nhóm 20 học sinh dùng một thiết bị đo đường kính của một nhân tế bào cho kết quả như sau:

a) Tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

b) Số trung bình và độ lệch chuẩn cho biết thông tin gì?

Lời giải:

Chọn giá trị đại diện cho mẫu số liệu ta có:

a) $\overline{x}=\frac{\mathrm{4,75.3}+\mathrm{5,25.8}+\mathrm{5,75.7}+\mathrm{6,25.2}}{20}=\mathrm{5,45}$.

$s^2=\frac{{\mathrm{4,75}}^2.3+{\mathrm{5,25}}^2.8+{\mathrm{5,75}}^2.7+{\mathrm{6,25}}^2.2}{20}-{\mathrm{5,45}}^2=\mathrm{0,185}$.

$s=\sqrt{\mathrm{0,185}}\approx \mathrm{0,43}$.

b) Dữ liệu cho thấy đường kính của các nhân tế bào có mức độ biến động nhỏ và gần giá trị trung bình. Điều này có thể thấy được mức độ đồng đều trong kích thước của các nhân tế bào hoặc quy trình đo lường được thực hiện một cách chính xác.

Bài 3.7 trang 84 Toán 12 Tập 1: Thời gian chạy tập luyện cự li 100m cuả hai vận động viên được cho trong bảng sau:

Dựa trên độ lệch chuẩn của các mẫu số liệu ghép nhóm, hãy cho biết vận động viên nào có thành tích luyện tập ổn định hơn.

Lời giải:

Chọn giá trị đại diện cho mẫu số liệu ta có:

Thời gian chạy trung bình của A là:

$\overline{x_A}=\frac{\mathrm{10,15.2}+\mathrm{10,45.10}+\mathrm{10,75.5}+\mathrm{11,05.3}}{20}=\mathrm{10,585}$.

Thời gian chạy trung bình của B là:

$\overline{x_B}=\frac{\mathrm{10,15.3}+\mathrm{10,45.7}+\mathrm{10,75.9}+\mathrm{11,05.6}}{25}=\mathrm{10,666}$.

Phương sai và độ lệch chuẩn của A là

$s_A^2=\frac{{\mathrm{10,15}}^2.2+{\mathrm{10,45}}^2.10+{\mathrm{10,75}}^2.5+{\mathrm{11,05}}^2.3}{20}-{\mathrm{10,585}}^2\approx \mathrm{0,067}$.

Suy ra $s_A=\sqrt{\mathrm{0,067}}\approx \mathrm{0,26}$.

Phương sai và độ lệch chuẩn của B là

$s_B^2=\frac{{\mathrm{10,15}}^2.3+{\mathrm{10,45}}^2.7+{\mathrm{10,75}}^2.9+{\mathrm{11,05}}^2.6}{25}-{\mathrm{10,666}}^2\approx \mathrm{0,083}$.

Suy ra $s_B=\sqrt{\mathrm{0,083}}\approx \mathrm{0,29}$.

Vận động viên A có độ lệch chuẩn nhỏ hơn so với vận động viên B. Điều này cho thấy thời gian chạy tập luyện của vận động viên A ít biến động hơn so với vận động viên B. Do đó vận động viên A có thành tích luyện tập ổn định hơn so với vận động viên B.

Bài 3.8 trang 84 Toán 12 Tập 1: Có nên dùng phương sai (hoặc độ lệch chuẩn) để so sánh độ phân tán của hai mẫu số liệu ghép nhóm trong mỗi trường hợp sau không? Tại sao?

a) Các mẫu số liệu ghép nhóm về điểm thi tốt nghiệp môn Toán của học sinh hai trường trung học phổ thông có chất lượng tương đương.

b) Các mẫu số liệu ghép nhóm về doanh thu của 100 cửa hàng bán lẻ và doanh thu của 100 siêu thị.

Lời giải:

a) Trong trường hợp các mẫu số liệu ghép nhóm về đểm thi tốt nghiệp môn Toán của học sinh hai trường trung học phổ thông có chất lượng tương đương, phương sai hoặc độ lệch chuẩn có thể được sử dụng để so sánh độ phân tán của hai mẫu số liệu vì chất lượng hai trường là tương đương. Dùng phương sai hoặc độ lệch chuẩn giúp đánh giá mức độ biến động của điểm thi từ đó so sánh độ phân tán giữa hai trường.

b) Trong trường hợp này việc sử dụng phương sai hoặc độ lệch chuẩn để so sánh độ phân tán có thể không phản ánh đúng bản chất của dữ liệu. Vì doanh thu thường có phân phối không đồng đều, có nhiều yếu tố ảnh hưởng đến doanh thu của từng cửa hàng hoặc siêu thị. Do đó việc sử dụng phương sai hoặc độ lệch chuẩn không phải là phương pháp phù hợp để so sánh độ phân tán của doanh thu của hai nhóm này.

Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 9. Khoảng biến thiên và khoảng tứ phân vị

Bài 10. Phương sai và độ lệch chuẩn

Bài tập cuối chương 3

Khảo sát và vẽ đồ thị hàm số với phần mềm GeoGebra

Vẽ vectơ tổng của ba vectơ trong không gian bằng phần mêm GeoGebra

Độ dài gang tay (gang tay của bạn dài bao nhiêu?)

Lý thuyết Phương sai và độ lệch chuẩn

1. Phương sai và độ lệch chuẩn

Cho mẫu số liệu ghép nhóm:

trong đó các tần số $m_1>0,m_k>0$ và $n=m_1+...+m_k$ là cỡ mẫu

Ý nghĩa: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán

2. Sử dụng phương sai, độ lệch chuẩn đo độ rủi ro

Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?

Giải:

Chọn giá trị đại diện cho các nhóm số liệu ta có:

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:

$\overline{x_A}=\frac{1}{60}(5.7,5+...+5.27,5)=17,5$ (triệu đồng)

$\overline{x_B}=\frac{1}{60}(20.7,5+...+20.27,5)=17,5$ (triệu đồng)

Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau

Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:

$s_A=\sqrt{\frac{1}{60}(5.7,5^2+...+5.27,5^2-17,5^2}=5$

$s_B=\sqrt{\frac{1}{60}(20.7,5^2+...+20.27,5^2-17,5^2}\approx 8,42$

Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn