Giải SGK Toán 7 (Chân trời sáng tạo) Bài tập cuối chương 7

Nguyễn Thị Thuỳ Linh Ngày: 22-09-2024 Lớp 7

4.3 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 7 chi tiết sách Toán 7 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 7

Giải Toán 7 trang 42 Tập 2

Bài 1 trang 42 Toán lớp 7: Cho $A = x^{2} y + 2 x y - 3 y^{2} + 4$ . Tính giá trị của biểu thức A khi x = -2, y = 3.

Phương pháp giải:

Ta thay các x, y đề bài cho trước vào biểu thức rồi tính

Lời giải:

$A = x^{2} y + 2 x y - 3 y^{2} + 4$

Thay các x = -2 và y = 3 vào công thức ta có :

$\begin{array}{l} A = (- 2)^{2} .3 + 2 (- 2) .3 - {3.3}^{2} + 4 \\ = 4.3 - 12 - 27 + 4 \\ = - 23 \end{array}$

Bài 2 trang 42 Toán lớp 7: Trong các biểu thức sau, biểu thức nào là đơn thức một biến ?

a) 2y b) 3x + 5

c) 8 d) $21 t^{12}$

Phương pháp giải:

Định nghĩa đa thức một biến.

Lời giải:

Các đa thức 1 biến là a, c, d

Bài 3 trang 42 Toán lớp 7: Trong các biểu thức sau, biểu thức nào là đa thức một biến ?

$3 + 6 y$ ; $7 x^{2} + 2 x - 4 x^{4} + 1$ ;

$\frac{2}{x + 1}$ ; $\frac{1}{3} x - 5$ .

Phương pháp giải:

- Dựa vào định nghĩa của đa thức 1 biến

Lời giải:

Các đa thức 1 biến là :

$3 + 6 y; 7 x^{2} + 2 x - 4 x^{4} + 1; \frac{1}{3} x - 5$

Bài 4 trang 42 Toán lớp 7: Hãy viết một đa thức một biến bậc ba có 3 số hạng.

Phương pháp giải:

- Sử dụng các định nghĩa về bậc trong đa thức 1 biến

Lời giải:

$x^{3} + 2 x - 1$

Chú ý : Có nhiều cách khác nhau để viết đa thức nhưng trong bài này các số hạng trong đa thức luôn luôn là 3

Bài 5 trang 42 Toán lớp 7: Hãy cho biết bậc của các đa thức sau:

$A = 3 x - 4 x^{2} + 1$

$B = 7$

$M = x - 7 x^{3} + 10 x^{4} + 2$

Phương pháp giải:

Dựa vào các định nghĩa về bậc trong đa thức

Lời giải:

A có bậc là 2

B có bậc là 0

M có bậc là 4

Bài 6 trang 42 Toán lớp 7: Cho đa thức P(x) = $x^{3} + 27$ . Tìm nghiệm của P(x) trong tập hợp ${0; 3; - 3}$

Phương pháp giải:

Ta xét P(x) = 0 rồi tìm x. Giá trị x tìm được là nghiệm của đa thức

Lời giải:

Xét P(x) = $x^{3} + 27 = 0$

$\begin{array}{l} \Leftrightarrow x^{3} = - 27 \\ \Leftrightarrow x^{3} = - 27 = (- 3)^{3} \\ \Rightarrow x = - 3 \end{array}$

Vì $- 3 \in {0; 3; - 3}$ nên -3 là 1 nghiệm

Bài 7 trang 42 Toán lớp 7: Tam giác trong Hình 1 có chu vi bằng (25y – 8) cm. Tìm cạnh chưa biết trong tam giác đó.

Bài 7 trang 42 Toán lớp 7 Tập 2 | Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Ta tính cạnh còn lại bằng cách lấy chu vi trừ đi 2 cạnh còn lại đã biết
Sử dụng qui tắc cộng trừ đa thức

Lời giải:

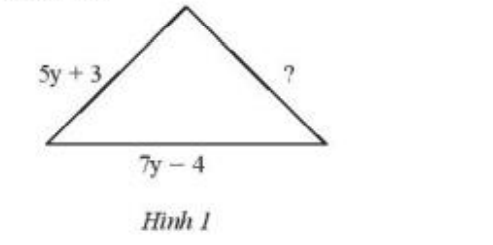
Theo đề bài ta có chu vi hình tam giác = 25y – 8 cm

Ta có 2 cạnh của tam giác đã biết theo đề bài

$\Rightarrow$ Cạnh còn lại cần tìm của tam giác là : 25y – 8 – 5y + 3 – 7y + 4 = 13y – 7 cm

Bài 8 trang 42 Toán lớp 7: Cho đa thức $M (x) = 2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x$ .

Tìm các đa thức N(x), Q(x) sao cho:

$N (x) - M (x) = - 4 x^{4} - 2 x^{3} + 6 x^{2} + 7$

và $M (x) + Q (x) = 6 x^{5} - x^{4} + 3 x^{2} - 2$

Phương pháp giải:

Áp dụng qui tắc cộng trừ các đa thức 1 biến

Lời giải:

Theo đề bài ta có $M (x) = 2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x$

$\begin{array}{l} M (x) + Q (x) = 6 x^{5} - x^{4} + 3 x^{2} - 2 \\ \Rightarrow Q (x) = (6 x^{5} - x^{4} + 3 x^{2} - 2) - (2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x) \\ \Rightarrow Q (x) = 6 x^{5} - x^{4} + 3 x^{2} - 2 - 2 x^{4} + 5 x^{3} - 7 x^{2} - 3 x \\ Q (x) = 6 x^{5} - 3 x^{4} + 5 x^{3} - 4 x^{2} - 3 x - 2 \end{array}$

Theo đề bài ta có :

$\begin{array}{l} N (x) - M (x) = - 4 x^{4} - 2 x^{3} + 6 x^{2} + 7 \\ \Rightarrow N (x) = - 4 x^{4} - 2 x^{3} + 6 x^{2} + 7 + 2 x^{4} - 5 x^{3} + 7 x^{2} + 3 x \\ \Rightarrow N (x) = - 2 x^{4} - 7 x^{3} + 13 x^{2} + 3 x + 7 \end{array}$

Bài 9 trang 42 Toán lớp 7: Thực hiện phép nhân.

a) $(3 x - 2) (4 x + 5)$

b) $(x^{2} - 5 x + 4) (6 x + 1)$

Phương pháp giải:

Áp dụng qui tắc nhân 2 đa thức 1 biến

Lời giải:

a) $(3 x - 2) (4 x + 5)$

$\begin{array}{l} = 3 x (4 x + 5) - 2 (4 x + 5) \\ = 3 x .4 x + 5.3 x - 2.4 x - 2.5 \\ = 12 x^{2} + 7 x - 10 \end{array}$

b) $(x^{2} - 5 x + 4) (6 x + 1)$

$\begin{array}{l} = x^{2} (6 x + 1) - 5 x (6 x + 1) + 4 (6 x + 1) \\ = x^{2} .6 x + 1. x^{2} - 5 x .6 x - 5 x .1 + 4.6 x + 4.1 \end{array}$

$= 6 x^{3} - 29 x^{2} + 19 x + 4$

Bài 10 trang 42 Toán lớp 7: Thực hiện phép chia.

a) $(45 x^{5} - 5 x^{4} + 10 x^{2}) : 5 x^{2}$

b) $(9 t^{2} - 3 t^{4} + 27 t^{5}) : 3 t$

Phương pháp giải:

Thực hiện phép tính bằng qui tắc chia đa thức
Ta có thể chia theo cột nhưng cần sắp xếp các đa thức theo thứ tự lũy thừa giảm dần

Lời giải:

a) $(45 x^{5} - 5 x^{4} + 10 x^{2}) : 5 x^{2}$ $= 9 x^{3} - x^{2} + 2$

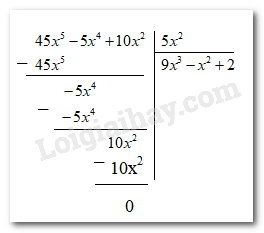
Bài 10 trang 42 Toán lớp 7 Tập 2 | Chân trời sáng tạo (ảnh 1)

b) $(9 t^{2} - 3 t^{4} + 27 t^{5}) : 3 t = (27 t^{5} - 3 t^{4} + 9 t^{2}) : 3 t = (27 t^{5}) : (3 t) - (3 t^{4}) : (3 t) + (9 t^{2}) : (3 t) = 9 t^{4} - 3 t^{3} + 3 t$

Bài 11 trang 42 Toán lớp 7: Thực hiện phép chia.

a) $(2 y^{4} - 13 y^{3} + 15 y^{2} + 11 y - 3) : (y^{2} - 4 y - 3)$

b) $(5 x^{3} - 3 x^{2} + 10) : (x^{2} + 1)$

Phương pháp giải:

Đặt tính và chia 2 đa thức

Ta sắp xếp các đa thức theo thứ tự giảm dần của lũy thừa để dễ thực hiện phép tính hơn

Lời giải:

Bài 11 trang 42 Toán lớp 7 Tập 2 | Chân trời sáng tạo (ảnh 1)

$a) (2 y^{4} - 13 y^{3} + 15 y^{2} + 11 y - 3) : (y^{2} - 4 y - 3) = 2 y^{2} - 5 y + 1$

b) $(5 x^{3} - 3 x^{2} + 10) : (x^{2} + 1) = 5 x - 3 + \frac{- 5 x + 13}{x^{2} + 1}$

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Bài 1: Biểu thức số và biểu thức đại số

Bài 2: Đa thức một biến

Bài 3: Phép cộng và phép trừ đa thức một biến

Bài 4: Phép nhân và phép chia đa thức một biến

Tổng hợp lý thuyết Toán 7 Chương 7

1. Biểu thức số

- Các số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa tạo thành một biểu thức.

Chẳng hạn: 3 + 7 – 2; 4. 5: 2; 2. (5 + 8) là những biểu thức.

Những biểu thức như trên còn được gọi là biểu thức số.

2. Biểu thức đại số

Biểu thức bao gồm các số và các chữ (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa được gọi là biểu thức đại số.

Trong biểu thức đại số:

- Những chữ đại diện cho một số tùy ý gọi là biến số;

- Những chữ đại diện cho một số xác định gọi là hằng số;

Chú ý:

- Trong biểu thức đại số, vì biến đại diện cho số nên khi thực hiện các phép tính trên các biến, ta có thể áp dụng những tính chất, quy tắc phép toán như trên các số. Chẳng hạn:

x + y = y + z;

(x + y) + z = x + (y + z);

(xy)z = x(yz);

xy = yx;

xxx = x³;

x(y + z) = xy + xz

3. Giá trị của biểu thức đại số

Để tính giá trị của một biểu thức đại số ta thực hiện các bước sau:

- Bước 1: Thay chữ bởi giá trị số đã cho (chú ý các trường hợp phải đặt số trong dấu ngoặc);

- Bước 2: Thực hiện các phép tính (chú ý đến thứ tự thực hiện các phép tính: thực hiện phép lũy thừa, rồi đến phép nhân chia, sau đó là phép cộng trừ).

4. Đa thức một biến

Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và biến đó.

Ta có thể thực hiện các phép tính cộng, trừ, nhân, chia đơn thức cùng một biến.

- Đa thức một biến là tổng của những đơn thức cùng một biến. Đơn thức một biến cũng là đa thức một biến.

Quy ước: P = 0 được gọi là đa thức không.

5. Cách biểu diễn đa thức một biến

- Để thuận tiện cho việc tính toán đối với các đa thức một biến, ta thường viết đa thức đó thành đa thức thu gọn và sắp xếp các đơn thức của chúng theo lũy thừa tăng hoặc giảm của biến.

- Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó.

Chú ý:

- Số thực khác 0 được gọi là đa thức bậc 0.

- Số 0 được gọi là đa thức không có bậc.

6. Giá trị của đa thức một biến

Để tính giá trị của đa thức một biến ta thực hiện các bước sau:

- Bước 1: Thay chữ bởi giá trị số đã cho (chú ý các trường hợp phải đặt số trong dấu ngoặc);

7. Nghiệm của đa thức một biến

Nếu đa thức P(x) có giá trị bằng 0 tại x = a thì ta nói a hoặc x = a là một nghiệm của đa thức đó.

Chú ý:

- Một đa thức (khác đa thức không) có thể có 1; 2; 3; ...; n nghiệm hoặc không có nghiệm nào.

- Số nghiệm của một đa thức (khác đa thức 0) không vượt qua bậc của nó.

8. Phép cộng hai đa thức một biến

Để cộng hai đa thức một biến, ta làm một trong hai cách sau:

- Cách 1: Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép cộng.

- Cách 2: Sắp xếp các đơn thức của hai đa thức cùng theo lũy thừa giảm dần (hoặc tăng dần) của biến rồi đặt phép tính theo cột dọc tương ứng sao cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau rồi thực hiện cộng theo cột.

9. Phép trừ hai đa thức một biến

Để trừ hai đa thức một biến, ta làm một trong hai cách sau:

- Cách 1:Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép trừ.

10. Tính chất của phép cộng đa thức một biến

Tính chất: Cho A, B, C là các đa thức một biến với cùng một biến số.

-Tính chất giao hoán: A + B = B + A;

-Tính chất kết hợp: A + (B + C) = (A + B) + C.

11. Phép nhân đa thức một biến

Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

12. Phép chia đa thức một biến

Trường hợp 1: Chia đa thức cho đa thức (chia hết)

Cho hai đa thức P và Q (với Q ≠ 0). Ta nói đa thức P chia hết cho đa thức Q nếu có đa thức M sao cho P = Q. M.

Ta gọi P là đa thức bị chia, Q là đa thức chia và M là đa thức thương (gọi tắt là thương).

Kí hiệu M = P : Q hoặc M = $\frac{P}{Q}$ .

Chú ý: Để thực hiện phép chia đa thức, người ta thường viết các đa thức đó thành đa thức thu gọn và sắp xếp các đơn thức theo lũy thừa giảm dần rồi thực hiện phép chia.

Trường hợp 2: Chia đa thức cho đa thức (phép chia có dư)

Khi chia đa thức A cho đa thức B với thương là Q, dư là R thì A = B. Q + R, trong đó bậc của R nhỏ hơn bậc của B.

13. Tính chất của phép nhân đa thức một biến

Tính chất: Cho A, B, C là các đa thức một biến với cùng một biến số.

-Tính chất giao hoán: A. B = B. A;

-Tính chất kết hợp: A. (B. C) = (A. B). C.