Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 2: Toạ độ của vectơ chi tiết sách Toán 12 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 2: Toạ độ của vectơ

Câu hỏi khởi động trang 65 Toán 12 Tập 1: Bão Haiyan (Hải Yến) là một cơn bão mạnh đã đổ bộ vào nước ta những ngày đầu tháng 11 năm 2013.

Để theo dõi đường đi của bão và vận tốc gió, người ta sử dụng tọa độ của các vectơ chỉ vận tốc của những luồng gió xoáy vào tâm bão (Hình 18).

Tọa độ của vectơ trong không gian là gì? Làm thế nào để xác định được tọa độ của vectơ trong không gian?

Lời giải:

Sau bài học này, ta sẽ trả lời được câu hỏi trên như sau:

- Trong không gian với hệ tọa độ Oxyz, tọa độ của một vectơ $\overrightarrow{u}$ là tọa độ của điểm A, trong đó A là điểm sao cho $\overrightarrow{OA}=\overrightarrow{u}$.

- Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{u}$ tùy ý. Bộ ba số (a; b; c) duy nhất sao cho $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}$ được gọi là tọa độ của vectơ $\overrightarrow{u}$ đối với hệ tọa độ Oxyz. Khi đó ta viết $\overrightarrow{u}=\left(a;b;c\right)$.

Hoạt động 1 trang 65 Toán 12 Tập 1: Trong không gian, hãy vẽ:

a) Ba trục số Ox, Oy, Oz vuông góc với nhau từng đôi một và cắt nhau tại gốc O của mỗi trục.

b)

- Vectơ $\overrightarrow{i}$ xuất phát từ điểm gốc O, theo chiều dương của trục Ox và có độ dài bằng 1.

- Vectơ $\overrightarrow{j}$ xuất phát từ điểm gốc O, theo chiều dương của trục Oy và có độ dài bằng 1.

- Vectơ $\overrightarrow{k}$ xuất phát từ điểm gốc O, theo chiều dương của trục Oz và có độ dài bằng 1.

Lời giải:

a)

b) Ta vẽ như hình dưới đây.

Luyện tập 1 trang 66 Toán 12 Tập 1: Một căn phòng với hệ tọa độ Oxyz được chọn như Hình 21. Cho biết bức tường phía sau của căn phòng nằm trong mặt phẳng tọa độ nào.

Lời giải:

Bức tường phía sau của căn phòng nằm trong mặt phẳng tọa độ (Oxz).

Hoạt động 2 trang 66 Toán 12 Tập 1: Cho điểm M trong không gian với hệ toạ độ Oxyz. Gọi M₁ là hình chiếu của điểm M trên mặt phẳng (Oxy) (Hình 22).

a) Trong mặt phẳng (Oxy) hãy cho biết:

- Hình chiếu H của điểm M trên trục hoành Ox ứng với số nào trên trục Ox?

- Hình chiếu K của điểm M trên trục tung Oy ứng với số nào trên trục Oy?

b) Hình chiếu P của điểm M trên trục cao Oz ứng với số nào trên trục Oz?

Lời giải:

Quan sát Hình 22, ta thấy:

a) Trong mặt phẳng (Oxy):

- Hình chiếu H của điểm M trên trục hoành Ox ứng với số 4 trên trục Ox.

- Hình chiếu K của điểm M trên trục tung Oy ứng với số 5 trên trục Oy.

b) Hình chiếu P của điểm M trên trục cao Oz ứng với số 3 trên trục Oz.

Luyện tập 2 trang 67 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho điểm A(3; 2; 4). Gọi H, K, P lần lượt là hình chiếu của điểm A trên các trục Ox, Oy, Oz. Tìm tọa độ của các điểm H, K, P.

Lời giải:

Gọi H(x₁; y₁; z₁), K(x₂; y₂; z₂) và P(x₃; y₃; z₃).

Với A(3; 2; 4), đặt x_A = 3, y_A = 2, z_A = 4. Ta có:

+ x₁ = x_A = 3; y₁ = 0; z₁ = 0 (vì H nằm trên trục Ox). Do đó H(3; 0; 0).

+ y₂ = y_A = 2; x₂ = 0; z₂ = 0 (vì K nằm trên trục Oy). Do đó K(0; 2; 0).

+ z₃ = z_A = 4; x₃ = 0; y₃ = 0 (vì P nằm trên trục Oz). Do đó P(0; 0; 4).

Hoạt động 3 trang 68 Toán 12 Tập 1: Cho điểm M trong không gian với hệ tọa độ Oxyz.

a) Vẽ vectơ $\overrightarrow{OM}$ .

b) Nêu cách xác định tọa độ của điểm M.

Lời giải:

a) Các bước vẽ vectơ $\overrightarrow{OM}$ như sau:

- Vẽ hệ trục tọa độ Oxyz.

- Lấy điểm M bất kì trong hệ tọa độ Oxyz.

- Nối O với M tạo thành vectơ $\overrightarrow{OM}$.

b) Cách xác định tọa độ của điểm M:

- Xác định hình chiếu M₁ của điểm M trên mặt phẳng (Oxy). Trong mặt phẳng tọa độ (Oxy), tìm hoành độ a, tung độ b của điểm M₁.

- Xác định hình chiếu P của điểm M trên trục cao Oz, điểm P ứng với số c trên trục Oz. Số c là cao độ của điểm M.

Vậy M(a; b; c).

Luyện tập 3 trang 68 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{OA}=\left(3;1;-2\right)$. Tìm tọa độ điểm A.

Lời giải:

Ta có $\overrightarrow{OA}=\left(3;1;-2\right)$. Do đó A(3; 1; – 2).

Hoạt động 4 trang 69 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{u}$ (Hình 28). Hãy xác định điểm A sao cho $\overrightarrow{OA}=\overrightarrow{u}$ (Hình 29).

Lời giải:

Cách xác định điểm A:

- Từ gốc tọa độ O, dựng đường thẳng d song song với giá của vectơ $\overrightarrow{u}$.

- Trên d, lấy điểm A sao cho vectơ $\overrightarrow{OA}$ cùng hướng với vectơ $\ov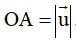errightarrow{u}$ và .

Vậy ta được điểm A thỏa mãn $\overrightarrow{OA}=\overrightarrow{u}$.

Luyện tập 4 trang 69 Toán 12 Tập 1: Tìm tọa độ của các vectơ $\overrightarrow{KA},\overrightarrow{A_{3}A}$ ở Hình 30.

Lời giải:

Trong Hình 30, ta có: $\overrightarrow{KA}=\overrightarrow{O{A}_3}$, $\overrightarrow{A_{3}A}=\overrightarrow{OK}$, mà A₃(4; 0; 3) và K(0; 5; 0).

Do đó, $\overrightarrow{KA}=\left(4;0;3\right)$ và $\overrightarrow{A_{3}A}=\left(0;5;0\right)$.

Hoạt động 5 trang 70 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{u}=\left(a;b;c\right)$(Hình 31). Lấy điểm A sao cho $\overrightarrow{OA}=\overrightarrow{u}$.

a) Tìm hoành độ, tung độ và cao độ của điểm A.

b) Biểu diễn vectơ $\overrightarrow{OH}$ qua vectơ $\overrightarrow{i}$; vectơ $\overrightarrow{OK}$ qua vectơ $\overrightarrow{j}$; vectơ $\overrightarrow{OP}$ qua vectơ $\overrightarrow{k}$.

c) Biểu diễn vectơ $\overrightarrow{u}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$.

Lời giải:

a) Ta có $\overrightarrow{OA}=\overrightarrow{u}$, mà $\overrightarrow{u}=\left(a;b;c\right)$ nên $\overrightarrow{OA}=\left(a;b;c\right)$.

Do đó, A(a; b; c). Vậy điểm A có hoành độ a, tung độ b và cao độ c.

b) Ta có $\overrightarrow{OH}=a\overrightarrow{i};\overrightarrow{OK}=b\overrightarrow{j};\overrightarrow{OP}=c\overrightarrow{k}$.

c) Theo quy tắc hình bình hành, ta có $\overrightarrow{O{A}_1}=\overrightarrow{OH}+\overrightarrow{OK}$ và $\overrightarrow{OA}=\overrightarrow{O{A}_1}+\overrightarrow{OP}$.

Suy ra $\overrightarrow{OA}=\overrightarrow{OH}+\overrightarrow{OK}+\overrightarrow{OP}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}$.

Mà $\overrightarrow{OA}=\overrightarrow{u}$. Do đó, $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}$.

Luyện tập 5 trang 70 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{OB}=-\overrightarrow{i}+2\overrightarrow{k}$ và vectơ $\overrightarrow{v}=-7\overrightarrow{j}+\overrightarrow{k}$. Hãy tìm tọa độ của:

a) Điểm B;

b) Vectơ $\overrightarrow{v}$.

Lời giải:

a) Ta có $\overrightarrow{OB}=-\overrightarrow{i}+2\overrightarrow{k}=\left(-1\right)\overrightarrow{i}+0\overrightarrow{j}+2\overrightarrow{k}$.

Do đó, $\overrightarrow{OB}=\left(-1;0;2\right)$. Vậy B(– 1; 0; 2).

b) Ta có $\overrightarrow{v}=-7\overrightarrow{j}+\overrightarrow{k}=0\overrightarrow{i}+\left(-7\right)\overrightarrow{j}+1\overrightarrow{k}$.

Do đó, $\overrightarrow{v}=\left(0;-7;1\right)$.

Hoạt động 6 trang 71 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(x_A; y_A; z_A), B(x_B; y_B; z_B­) (Hình 32).

a) Biểu diễn mỗi vectơ $\overrightarrow{OA},\overrightarrow{OB}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j}$ và $\overrightarrow{k}$.

b) Tìm liên hệ giữa $\overrightarrow{AB}$ và (x_B – x_A)$\overrightarrow{i}$ + (y_B – y_A)$\overrightarrow{j}$+ (z_B – z_A)$\overrightarrow{k}$.

c) Từ đó, tìm tọa độ của vectơ $\overrightarrow{AB}$ .

Lời giải:

a) Vì điểm A có tọa độ là (x_A; y_A; z_A) nên $\overrightarrow{OA}=\left(x_A;y_A;z_A\right)$ .

Do đó, $\overrightarrow{OA}=x_A\overrightarrow{i}+y_A\overrightarrow{j}+z_A\overrightarrow{k}$ .

Vì điểm B có tọa độ là (x_B; y_B; z_B­) nên $\overrightarrow{OB}=\left(x_B;y_B;z_B\right)$ .

Do đó, $\overrightarrow{OB}=x_B\overrightarrow{i}+y_B\overrightarrow{j}+z_B\overrightarrow{k}$ .

b) Theo quy tắc hiệu ta có

c) Ta có $\overrightarrow{AB}$ = (x_B – x_A)$\overrightarrow{i}$ + (y_B – y_A)$\overrightarrow{j}$+ (z_B – z_A)$\overrightarrow{k}$.

Do đó, $\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A;z_B-z_A\right)$ .

Luyện tập 6 trang 71 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A'(1; 0; 1), B'(2; 1; 2), D'(1; – 1; 1), C(4; 5; – 5). Tìm tọa độ đỉnh A của hình hộp ABCD.A'B'C'D'.

Lời giải:

Ta có $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$ = (2 – 1; 1 – 0; 2 – 1) = (1; 1; 1).

Gọi tọa độ của điểm C' là (x_C'; y_C'; z_C'), ta có $\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$ = (x_C' – 1; y_C' – (– 1); z_C' – 1).

Vì ABCD.A'B'C'D' là hình hộp nên A'B'C'D' là hình bình hành.

Do đó, $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}=\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$ . Suy ra 

Khi đó, C'(2; 0; 2).

Ta có $\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ = (2 – 1; 0 – 0; 2 – 1) = (1; 0; 1).

Gọi tọa độ của điểm A là (x_A; y_A; z_A), ta có $\overrightarrow{AC}=\left(4-x_A;5-y_A;-5-z_A\right)$ .

Vì ABCD.A'B'C'D' là hình hộp nên $\overrightarrow{AC}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ .

Do đó, 

Vậy A(3; 5; – 6).

Bài tập

Bài 1 trang 72 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3). Tọa độ của vectơ $\overrightarrow{OA}$ là:

A. (1; 2; 3).

B. (1; 0; 3).

C. (0; 2; 3).

D. (1; 2; 0).

Lời giải:

Đáp án đúng là: A

Ta có A(1; 2; 3). Do đó, $\overrightarrow{OA}=\left(1;2;3\right)$.

Bài 2 trang 72 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{u}=\left(-1;4;2\right)$ và điểm A. Biết $\overrightarrow{OA}=\overrightarrow{u}$. Tọa độ của điểm A là:

A. (1; 4; 2).

B. (– 1; 4; 2).

C. (1; – 4; – 2).

D. (– 1; – 4; – 2).

Lời giải:

Đáp án đúng là: B

Vì $\overrightarrow{OA}=\overrightarrow{u}$, mà $\overrightarrow{u}=\left(-1;4;2\right)$, do đó $\overrightarrow{OA}=\left(-1;4;2\right)$.

Từ đó suy ra A(– 1; 4; 2).

Bài 3 trang 72 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{u}=-2\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k}$. Tọa độ của vectơ $\overrightarrow{u}$ là:

A. (– 2; – 1; 3).

B. (2; 1; 3).

C. (– 2; 0; 3).

D. (– 2; – 1; – 3).

Lời giải:

Đáp án đúng là: A

Ta có $\overrightarrow{u}=-2\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k}=\left(-2\right)\overrightarrow{i}+\left(-1\right)\overrightarrow{j}+3\overrightarrow{k}$.

Do đó, $\overrightarrow{u}=\left(-2;-1;3\right)$.

Bài 4 trang 72 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; – 1; 2) và B(4; – 3; 1). Tọa độ của vectơ $\overrightarrow{AB}$ là:

A. (– 3; 2; 1).

B. (3; – 2; – 1).

C. (5; – 4; 3).

D. (3; – 4; – 1).

Lời giải:

Đáp án đúng là: B

Với A(1; – 1; 2) và B(4; – 3; 1), ta có

$\overrightarrow{AB}$ = (4 – 1; – 3 – (– 1); 1 – 2) = (3; – 2; – 1).

Bài 5 trang 73 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho vectơ $\overrightarrow{u}=\left(4;2;3\right)$ và điểm A(1; 1; 1). Tọa độ điểm C thỏa mãn $\overrightarrow{AC}=\overrightarrow{u}$ là:

A. (4; 2; 3).

B. (1; 1; 1).

C. (5; 3; 4).

D. (3; 1; 2).

Lời giải:

Đáp án đúng là: C

Gọi tọa độ điểm C là (x_C; y_C; z_C), ta có $\overrightarrow{AC}$ = (x_C – 1; y_C – 1; z_C – 1).

Với $\overrightarrow{u}=\left(4;2;3\right)$ thì ta có $\overrightarrow{AC}=\overrightarrow{u}$ 

Vậy C(5; 3; 4).

Bài 6 trang 73 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho A(3; – 2 ; – 1). Gọi A₁, A₂, A₃ lần lượt là hình chiếu của điểm A trên các mặt phẳng toạ độ (Oxy), (Oyz), (Ozx). Tìm toạ độ của các điểm A₁, A₂, A₃

Lời giải:

Gọi A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂) và A₃(x₃; y₃; z₃).

Với A(3; – 2; – 1), đặt x_A = 3, y_A = – 2, z_A = – 1. Ta có:

+ x₁ = x_A = 3; y₁ = y_A = – 2; z₁ = 0 (vì A­₁ nằm trên mặt phẳng (Oxy)).

Do đó A₁(3; – 2; 0).

+ y₂ = y_A = – 2; z₂ = z_A = – 1; x₂ = 0 (vì A₂ nằm trên mặt phẳng (Oyz)).

Do đó A₂(0; – 2; – 1).

+ x₃ = x_A = 3; z₃ = z_A = – 1; y₃ = 0 (vì A₃ nằm trên mặt phẳng (Ozx)).

Do đó A₃(3; 0; – 1).

Bài 7 trang 73 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz,cho A(– 2; 3; 4). Gọi H, K, P lần lượt là hình chiếu của điểm A trên các trục Ox, Oy, Oz. Tìm toạ độ của các điểm H, K, P

Lời giải:

Gọi H(x₁; y₁; z₁), K(x₂; y₂; z₂) và P(x₃; y₃; z₃).

Với A(– 2; 3; 4), đặt x_A = – 2, y_A = 3, z_A = 4. Ta có:

+ x₁ = x_A = – 2; y₁ = 0; z₁ = 0 (vì H nằm trên trục Ox). Do đó H(– 2; 0; 0).

+ y₂ = y_A = 3; x₂ = 0; z₂ = 0 (vì K nằm trên trục Oy). Do đó K(0; 3; 0).

+ z₃ = z_A = 4; x₃ = 0; y₃ = 0 (vì P nằm trên trục Oz). Do đó P(0; 0; 4).

Bài 8 trang 73 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A(4; 6; – 5), B(5; 7; – 4), C(5; 6; – 4), D'(2; 0; 2). Tìm toạ độ các đỉnh còn lại của hình hộp ABCD.A'B'C'D'

Lời giải:

Ta có $\overrightarrow{AB}$ = (5 – 4; 7 – 6; – 4 – (– 5)) = (1; 1; 1).

Gọi tọa độ của điểm D là (x_D; y_D; z_D), ta có $\overrightarrow{DC}$ = (5 – x_D; 6 – y_D; – 4 – z_D).

Vì ABCD.A'B'C'D' là hình hộp nên ABCD là hình bình hành.

Do đó, $\overrightarrow{AB}=\overrightarrow{DC}$ . Suy ra 

Khi đó, D(4; 5; – 5).

Ta có $\overrightarrow{D{D}^{\text{'}}}$ = (2 – 4; 0 – 5; 2 – (– 5)) = (– 2; – 5; 7).

Gọi tọa độ của điểm A' là (x_A'; y_A'; z_A'), ta có $\overrightarrow{A{A}^{\text{'}}}$ = (x_A' – 4; y_A' – 6; z_A' – (– 5)).

Ta có 

Suy ra A'(2; 1; 2).

Gọi tọa độ của điểm B' là (x_B'; y_B'; z_B'), ta có $\overrightarrow{B{B}^{\text{'}}}$ = (x_B' – 5; y_B' – 7; z_B' – (– 4)).

Ta có 

Suy ra B'(3; 2; 3).

Gọi tọa độ của điểm C' là (x_C'; y_C'; z_C'), ta có $\overrightarrow{C{C}^{\text{'}}}$ = (x_C' – 5; y_C' – 6; z_B' – (– 4)).

Ta có 

Suy ra C'(3; 1; 3).

Vậy D(4; 5; – 5), A'(2; 1; 2), B'(3; 2; 3), C'(3; 1; 3).

Bài 9 trang 73 Toán 12 Tập 1: Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.

Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ Oxyz (đơn vị độ dài trên mỗi trục là l m), các đỉnh của bốn chiếc cột lần lượt là các điểm M(90; 0; 30), N(90; 120; 30), P(0; 120; 30), Q(0; 0; 30) (Hình 34).

Giả sử K₀ là vị trí ban đầu của camera có cao độ bằng 25 và K₀M = K₀N = K₀P = K₀Q. Để theo dõi quả bóng đến vị trí A, camera được hạ thấp theo phương thẳng đứng xuống điểm K₁ có cao độ bằng 19 (Nguồn: https:⁄/www.abiturloesumg.de; Abitur Bayern 2016 Geometrie VI).

Tìm tọa độ của các điểm K₀, K₁ và của vectơ $\overrightarrow{K_0{K}_1}$.

Lời giải:

Gọi M₁, N₁, P₁, K lần lượt là hình chiếu của M, N, P, K₀ lên mặt phẳng (Oxy).

Ta thấy MNPQ.M₁N₁P₁O là hình hộp chữ nhật.

Gọi K' là giao hai đường chéo MP và NQ. Khi đó K'Q = K'P = K'N = K'M.

Vì K₀M = K₀N = K₀P = K₀Q và camera được hạ thấp theo phương thẳng đứng từ điểm K₀ xuống điểm K₁ nên các điểm K', K₀, K₁, K thẳng hàng.

Khi đó, các điểm K', K₀, K₁, K có hoành độ và tung độ bằng nhau.

Theo bài ra, cao độ của K₀ và K₁ lần lượt là 25 và 19.

Giả sử K₀(x; y; 25) và K₁(x; y; 19).

Ta có MNPQ.M₁N₁P₁O là hình hộp chữ nhật nên K'K = OQ, suy ra cao độ của K' bằng 30. Do đó, K' (x; y; 30).

Ta có $\overrightarrow{K^{\text{'}}Q}=\left(-x;-y;0\right),\overrightarrow{N{K}^{\text{'}}}=\left(x-90;y-120;0\right)$ .

Vì K' là giao hai đường chéo của hình chữ nhật MMPQ nên K' là trung điểm của NQ.

Suy ra 

Do vậy, K₀(45; 60; 25), K₁(45; 60; 19) và $\overrightarrow{K_0{K}_1}=\left(0;0;-6\right)$.

Xem thêm các bài giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

§1. Vectơ và các phép toán vectơ trong không gian

§2. Toạ độ của vectơ

§3. Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

§1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

§2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

Lý thuyết Toạ độ của vectơ

1. Tọa độ của một điểm

a) Hệ trục tọa độ trong không gian

Hệ gồm ba trục Ox, Oy, Oz đôi một vuông góc được gọi là hệ trục tọa độ vuông góc Oxyz trong không gian, hay đơn giản gọi là hệ tọa độ Oxyz.

b) Tọa độ của một điểm

Trong không gian với hệ tọa độ Oxyz, cho điểm M. - Xác định hình chiếu $M_1$ của điểm M trên mặt phẳng (Oxy). Trong mặt phẳng tọa độ (Oxy), tìm hoành độ a, tung độ b của điểm $M_1$ - Xác định hình chiếu P của điểm M trên trục cao Oz, điểm P ứng với số c trên trục Oz. Số c là cao độ của điểm M. Bộ số (a;b;c) là tọa độ của điểm M trong không gian với hệ tọa độ Oxyz, kí hiệu là M(a;b;c)

2. Tọa độ của một vecto

Tọa độ của điểm M được gọi là tọa độ của vecto $\overrightarrow{OM}$ Trong không gian với hệ tọa độ Oxyz, tọa độ của một vecto $\overrightarrow{u}$ là tọa độ của điểm A, trong đó A là điểm sao cho $\overrightarrow{OA}=\overrightarrow{u}$ Trong không gian với hệ tọa độ Oxyz, nếu $\overrightarrow{u}$ = (a;b;c) thì$$\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}$$. Ngược lại, nếu$$\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}$$thì $\overrightarrow{u}$ = (a;b;c) Trong không gian với hệ tọa độ Oxyz, cho hai điểm $M(x_M;y_M;z_M)$ và $N(x_N;y_N;z_N)$. Khi đó: $\overrightarrow{MN}=(x_N-x_M;y_N-y_M;z_N-z_M)$

Ví dụ: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A’B’C có A(1;0;2), B(3;2;5), C(7;-3;9)

a)     Tìm tọa độ của $\overrightarrow{A{A}^{\prime }}$

b)    Tìm tọa độ của các điểm B’, C’

Lời giải

a)     Ta có: $\overrightarrow{A{A}^{\prime }}=(x_{A^{\prime }}-x_A;y_{A^{\prime }}-y_A;z_{A^{\prime }}-z_A)=(4;0;-1)$

b)    Gọi tọa độ của điểm B’ là (x,y,z) thì $\overrightarrow{B{B}^{\prime }}$ = (x-3;y-2;z-5). Vì ABC.A’B’C’ là hình lăng trụ nên ABB’A’ là hình bình hành, suy ra $\overrightarrow{A{A}^{\prime }}$ = $\overrightarrow{B{B}^{\prime }}$

Do đó $\{\begin{array}{l}x-3=4\\ y-2=0\\ z-5=-1\end{array}$ hay x = 7, y = 2, z = 4. Vậy B’(7;2;4)

Lập luận tương tự suy ra C’(11;-3;8)