Với lời giải Toán 11 trang 73 Tập 2 chi tiết trong Bài 3: Hai mặt phẳng vuông góc sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 3: Hai mặt phẳng vuông góc

Thực hành 5 trang 73 Toán 11 Tập 2: Cho hình chóp cụt tam giác đều ABC.A′B′C′ có cạnh đáy lớn bằng a, cạnh đáy nhỏ $\frac{a}{2}$ và cạnh bên 2a. Tính độ dài đường cao của hình chóp cụt đó.

Lời giải:

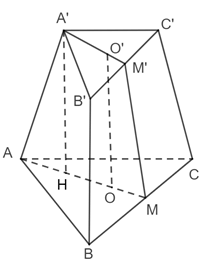
Gọi O, O′ lần lượt là tâm của hai đáy ABC và A′B′C′; M, M′ lần lượt là trung điểm của BC và B′C′.

Kẻ A′H ⊥ AO (H ∈ AO).

Khi đó, ta có A′H = OO′.

• ΔABC đều nên $\mathrm{AM}=\frac{\frac{a}{2}\cdot \sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\Rightarrow \mathrm{AO}=\frac{2}{3}\mathrm{AM}=\frac{a\sqrt{3}}{6}$.

• ΔA′B′C′ đều nên $A\text{'}M\text{'}=\frac{\frac{a}{2}.\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\Rightarrow A^{\text{'}}{O}^{\text{'}}=\frac{2}{3}{A}^{\text{'}}M\text{'}=\frac{a\sqrt{3}}{6}$.

• A′HOO′ là hình chữ nhật nên $\mathrm{OH}=A\text{'}O\text{'}=\frac{a\sqrt{3}}{6}$ $\Rightarrow \mathrm{AH}=\mathrm{AO}-\mathrm{OH}=\frac{a\sqrt{3}}{6}$.

• Tam giác AA′H vuông tại H nên ${\mathrm{OO}}^{\text{'}}=A^{\text{'}}H=\sqrt{{\mathrm{AA}}^{\text{'}2}-{\mathrm{AH}}^2}=\frac{a\sqrt{141}}{6}$.

Vận dụng 5 trang 73 Toán 11 Tập 2: Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn.

Lời giải:

Diện tích đáy lớn là: $6.\frac{1^2.\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}$(m²)

Diện tích đáy nhỏ là: $6.\frac{{\left(0,7\right)}^2.\sqrt{3}}{4}=\frac{147\sqrt{3}}{200}$(m²)

Một mặt bên của hình chóp cụt là hình thang cân có đáy lớn là 1 m, đáy nhỏ là 0,7 m và cạnh bên là 0,7 m.

Khi đó, chiều cao của mặt bên là: $\sqrt{0,7^2-{\left(\frac{1-0,7}{2}\right)}^2}=\frac{\sqrt{187}}{20}$ (m)

Diện tích một mặt bên là: $\frac{1}{2}$. $\frac{\sqrt{187}}{20}.\left(0,7+1\right)=0,58$(m²)

Vậy tổng diện tích cần sơn là: $\frac{3\sqrt{3}}{2}+\frac{147\sqrt{3}}{200}+6.0,58\approx 7,36$ (m²)

Bài tập

Bài 1 trang 73 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với (ABC).

a) Chứng minh rằng (SBC) ⊥ (SAC).

b) Gọi I là trung điểm của SC. Chứng minh rằng (ABI) ⊥ (SAC).

Lời giải:

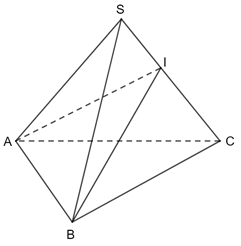
a) Ta có (SAC) ⊥ (ABC) ⇒ AC ⊥ (ABC) ⇒ AC ⊥ BC

Mà (SAC) ∩ (ABC) = AC nên BC ⊥ (SAC)

Do đó (SBC) ⊥ (SAC).

b) Ta có: BC ⊥ (SAC) nên BC ⊥ AI (AI ⊂ (SAC)) (1)

Tam giác SAC đều có I là trung điểm của SC nên AI ⊥ SC (2)

Từ (1) và (2) suy ra AI ⊥ (SBC)

Mà AI ⊂ (ABI) nên (ABI) ⊥ (SAC)

Bài 2 trang 73 Toán 11 Tập 2: Cho tam giác đều ABC cạnh a, I trung điểm của BC, D là điểm đối xứng với A qua I. Vẽ đoạn thẳng SD có độ dài $\frac{a\sqrt{6}}{2}$ và vuông góc với (ABC). Chứng minh rằng:

a) (SBC) ⊥ (SAD);

b) (SAB) ⊥ (SAC).

Lời giải:

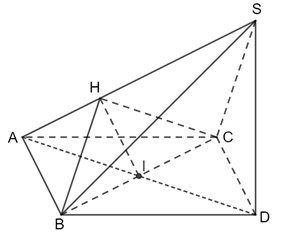
a) Tam giác ABC đều có I là trung điểm nên AI ⊥ CB hay AD ⊥ BC.

Vì SD ⊥ (ABC) ⇒ SD ⊥ BC.

⇒ BC ⊥ (SAD)

Nên (SAD) ⊥ (SBC)

b) Tam giác ABC đều nên $\mathrm{AI}=\frac{a\sqrt{3}}{3},\mathrm{AD}=a\sqrt{3}$

Ta có: ΔSAD vuông tại D nên $\mathrm{SA}=\sqrt{{\mathrm{AD}}^2+{\mathrm{SD}}^2}=\frac{3a\sqrt{2}}{2}$

Kẻ IH ⊥ SA.

Xét ΔAHI và ΔADS:

$\hat{A}$ chung

$\widehat{\mathrm{AHI}}=\widehat{\mathrm{ADS}}=90°$

Do đóΔAHI ᔕ ΔADS (g.g)

$\Rightarrow \frac{\mathrm{HI}}{\mathrm{DS}}=\frac{\mathrm{AI}}{\mathrm{AS}}\Rightarrow \mathrm{IH}=\frac{\mathrm{SD}.\mathrm{AI}}{\mathrm{AS}}=\frac{a}{2}$

Tam giác BHC có HI là trung tuyến và HI = $\frac{1}{2}$BC

⇒ ΔBHC vuông tại H.

Ta có: BC ⊥ (SAD) nên SA ⊥ BC.

Mà SA ⊥ HI nên SA ⊥ (HBC)

$\left.\begin{array}{c}\Rightarrow \mathrm{SA} \perp \mathrm{HB}\\ \mathrm{BH}\perp \mathrm{HC} \left(\mathrm{\Delta BHC}\perp \mathrm{H}\right)\end{array}\right\}\Rightarrow \mathrm{HB}\perp \left(\text{SAC}\right)$

Mà HB ⊂ (SAB)

⇒ (SAB) ⊥ (SAC)

Bài 3 trang 73 Toán 11 Tập 2: Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy ABCD là hình thang vuông tại A và B, AA′ = 2a, AD = 2a, AB = BC = a.

a) Tính độ dài đoạn thẳng AC′.

b) Tính tổng diện tích các mặt của hình lăng trụ.

Lời giải:

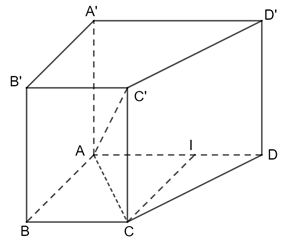
a) Ta có: $\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{AC}}^2}=a\sqrt{2}$

$\Rightarrow A^{\text{'}}C=\sqrt{{\mathrm{AC}}^2+C{C^{\text{'}}}^2}=a\sqrt{6}$

Vậy độ dài đoạn thẳng AC′ là $a\sqrt{6}$ .

b) $S_{\mathrm{ABCD}}=S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{2}\left(\mathrm{AD}+\mathrm{BC}\right)A.B=\frac{3a^2}{2}$

Gọi I là trung điểm của AD.

Khi đó ABCI là hình vuông nên IC = IB = IA = $\frac{1}{2}$AD = a

Xét tam giác ICD vuông cân tại I:

$\mathrm{CD}=\sqrt{{\mathrm{CI}}^2+{\mathrm{DI}}^2}=a\sqrt{2}$

$S_{{\mathrm{ABB}}^{\text{'}}{A}^{\text{'}}}=\mathrm{AB}.\mathrm{AA}\text{'}=2a^2$

$S_{{\mathrm{ADD}}^{\text{'}}{A}^{\text{'}}}=\mathrm{AD}.{\mathrm{AA}}^{\text{'}}=4a^2$

$S_{{\mathrm{BCC}}^{\text{'}}{B}^{\text{'}}}=\mathrm{BC}.{\mathrm{CC}}^{\text{'}}=2a^2$

$S_{{\mathrm{CDD}}^{\text{'}}{C}^{\text{'}}}=\mathrm{CD}.{\mathrm{CC}}^{\text{'}}=2a^2\sqrt{2}$

Tổng diện tích các mặt của hình lăng trụ là:

$S=S_{\mathrm{ABCD}}+S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}+S_{{\mathrm{ABB}}^{\text{'}}{A}^{\text{'}}}+S_{{\mathrm{ADD}}^{\text{'}}{A}^{\text{'}}}+S_{{\mathrm{BCC}}^{\text{'}}{B}^{\text{'}}}+S_{{\mathrm{CDD}}^{\text{'}}{C}^{\text{'}}}=\left(11+3\sqrt{2}\right)a^2$

Vậy tổng diện tích các mặt của hình lăng trụ là: $S=\left(11+3\sqrt{2}\right)a^2$