Với lời giải Toán 11 trang 94 Tập 2 chi tiết trong Bài 32: Các quy tắc tính đạo hàm sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 32: Các quy tắc tính đạo hàm

Luyện tập 7 trang 94 Toán 11 Tập 2: Tính đạo hàm của hàm số y = log₂(2x – 1).

Lời giải:

Điều kiện: 2x – 1 > 0 ⇔ x > $\frac{1}{2}$ . Hàm số đã cho xác định trên $\left(\frac{1}{2};+\infty \right)$ .

Ta có: $y^{\text{'}}=\frac{{\left(2x-1\right)}^{\text{'}}}{\left(2x-1\right)\ln 2}=\frac{2}{\left(2x-1\right)\ln 2}$ .

Vận dụng 2 trang 94 Toán 11 Tập 2: Ta đã biết, độ pH của một dung dịch được xác định bởi pH = –log[H⁺], ở đó [H⁺] là nồng độ (mol/lít) của ion hydrogen. Tính tốc độ thay đổi của pH đối với nồng độ [H⁺].

Lời giải:

Tốc độ thay đổi của pH với nồng độ [H⁺] là đạo hàm của pH. Ta có:

pH = –log[H⁺] ⇒ (pH)' = (–log[H⁺])' = 

Vậy tốc độ thay đổi của pH với nồng độ [H⁺] là .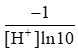

Bài tập

Bài 9.6 trang 94 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) y = x³ – 3x² + 2x + 1;

b) y = x² – 4$\sqrt{x}$ + 3.

Lời giải:

a)

y' = (x³)' – 3.(x²)' + 2.(x)' + 1' = 3x² – 6x + 2.

b) Với x > 0, ta có:

y' = (x²)' – 4. ($\sqrt{x}$) ' + 3' = 2x – $\frac{2}{\sqrt{x}}$ .

Bài 9.7 trang 94 Toán 11 Tập 2:Tính đạo hàm của các hàm số sau:

a) $y=\frac{2x-1}{x+2}$ ;

b) $y=\frac{2x}{x^2+1}$ .

Lời giải:

a) Với x ≠ – 2, ta có:

$y^{\text{'}}={\left(\frac{2x-1}{x+2}\right)}^{\text{'}}=\frac{(2x-1{)}^{\text{'}}.(x+2)-(2x-1).(x+2{)}^{\text{'}}}{{(x+2)}^2}$

$=\frac{2(x+2)-(2x-1)}{{(x+2)}^2}=\frac{5}{{(x+2)}^2}$.

b)

$y^{\text{'}}={\left(\frac{2x}{x^2+1}\right)}^{\text{'}}=\frac{\left(2x{)}^{\text{'}}\right(x^2+1)-2x.(x^2+1{)}^{\text{'}}}{{(x^2+1)}^2}$

$=\frac{2(x^2+1)-2x.2x}{{(x^2+1)}^2}=\frac{-2x^2+2}{{(x^2+1)}^2}$.

Bài 9.8 trang 94 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) y = xsin²x;

b) y = cos²x + sin2x;

c) y = sin3x – 3sinx;

d) y = tanx + cotx.

Lời giải:

a)

y' = (x)' . sin²x + x . (sin²x)' = sin²x + x . 2 . sinx . cosx = sin²x + xsin2x.

b)

y' = (cos²x)' + (sin2x)' = 2cosx.(–sinx) + 2cos2x

= –2cosx.sinx + 2cos2x = –sin2x + 2cos2x.

c)

y' = (sin3x)' – (3sinx)' = 3cos3x – 3cosx.

d) Với $x\ne k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ , ta có:

y' = (tanx)' + (cotx)' = $\frac{1}{{\cos }^{2}x}-\frac{1}{{\sin }^{2}x}$ .

Bài 9.9 trang 94 Toán 11 Tập 2: Tính đạo hàm các hàm số sau:

a) y = $2^{3x-x^2}$ ;

b) y = log₃(4x + 1).

Lời giải:

a) $y^{\text{'}}={\left(2^{3x-x^2}\right)}^{\text{'}}={\left(3x-x^2\right)}^{\text{'}}{.2}^{3x-x^2}.\ln 2=\left(3-2x\right){.2}^{3x-x^2}.\ln 2$ .

b) Với x>-$\frac{1}{4}$ , ta có:

$y^{\text{'}}={\log }_3\left(4x+1\right)=\frac{\left(4x+1\right)\text{'}}{\left(4x+1\right)\ln 3}=\frac{4}{\left(4x+1\right)\ln 3}$.

Bài 9.10 trang 94 Toán 11 Tập 2: Cho hàm số f(x) = $2{\sin }^2\left(3x-\frac{\pi }{4}\right)$ . Chứng minh rằng |f'(x)| ≤ 6 với mọi x.

Lời giải:

Ta có:

$f^{\text{'}}\left(x\right)=4\sin \left(3x-\frac{\pi }{4}\right)$.

$=\mathrm{4.3.}\cos \left(3x-\frac{\pi }{4}\right).\sin \left(3x-\frac{\pi }{4}\right)$

$=12\cos \left(3x-\frac{\pi }{4}\right).\sin \left(3x-\frac{\pi }{4}\right)=6\sin \left(6x-\frac{\pi }{2}\right)$

Vì:

$-1\le \sin \left(6x-\frac{\pi }{2}\right)\le 1\iff -6\le 6\sin \left(6x-\frac{\pi }{2}\right)\le 6$

⇔ –6 ≤ f'(x) ≤ 6 với mọi x.

Vậy |f'(x)| ≤ 6 với mọi x.

Bài 9.11 trang 94 Toán 11 Tập 2: Một vật chuyển động rơi tự do có phương trình h(t) = 100 – 4,9t², ở đó độ cao h so với mặt đất tính bằng mét và thời gian t tính bằng giây. Tính vận tốc của vật:

a) Tại thời điểm t = 5 giây;

b) Khi vật chạm đất.

Lời giải:

Ta có: v(t) = h'(t) = –9,8t.

a) Vận tốc tại thời điểm t = 5 giây là:

v(5) = –9,8 . 5 = –49 (m/s).

Vậy vận tốc của vật tại thời điểm t = 5s là 49 m/s.

b)

Khi vật chạm đất h(t) = 0, tức là 100 – 4,9t² = 0 $\Rightarrow t=\frac{10\sqrt{10}}{7}$ .

Vậy vận tốc của vật khi chạm đất là $v\left(\frac{10\sqrt{10}}{7}\right)=-9,8.\frac{10\sqrt{10}}{7}=-14\sqrt{10}$ (m/s).

Ở đây, dấu âm trong các kết quả tính vận tốc thể hiện vật chuyển động thẳng đứng xuống dưới (ngược với chiều dương).

Bài 9.12 trang 94 Toán 11 Tập 2: Chuyển động của một hạt trên một dây rung được cho bởi s(t) = 12 + 0,5sin(4πt), trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu ?

Lời giải:

Vận tốc của hạt sau t giây là:

v(t) = s'(t) = 0,5.(4πt)'.cos(4πt) = 2πcos(4πt) (m/s).

Vì –1 ≤ cos(4πt) ≤ 1 ⇔ –2π ≤ 2πcos(4πt) ≤ 2π ⇔ –2π ≤ v(t) ≤ 2π với mọi t.

Do đó vận tốc cực đại của hạt là 2π cm/s.