Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài tập cuối chương 9 chi tiết sách Toán 11 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài tập cuối chương 9

Bài tập

Giải Toán 11 trang 97 Tập 2

Bài 9.18 trang 97 Toán 11 Tập 2:Với u, v là các hàm số hợp theo biến x, quy tắc tính đạo hàm nào sau đây là đúng?

A. (u + v)' = u' – v'.

B. (uv)' = u'v + uv'.

C. ${\left(\frac{1}{v}\right)}^{\text{'}}=-\frac{1}{v^2}$ .

D. ${\left(\frac{u}{v}\right)}^{\text{'}}=\frac{u^{\text{'}}v+v^{\text{'}}u}{v^2}$ .

Lời giải:

Đáp án đúng là: B

Ta có quy tắc đạo hàm:

(u + v)' = u' + v'

(uv)' = u'v + uv'

${\left(\frac{1}{v}\right)}^{\text{'}}=-\frac{v^{\text{'}}}{v^2}$

${\left(\frac{u}{v}\right)}^{\text{'}}=\frac{u^{\text{'}}v-v^{\text{'}}u}{v^2}$

Vậy đáp án B đúng.

Bài 9.19 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = x² + sin³x. Khi đó $f^{\text{'}}\left(\frac{\pi }{2}\right)$ bằng

A. π.

B. 2π.

C. π + 3.

D. π – 3.

Lời giải:

Đáp án đúng là: A

Ta có: f'(x) = 2x + 3sin²xcosx

$\Rightarrow f^{\text{'}}\left(\frac{\pi }{2}\right)=2.\frac{\pi }{2}+2.{\sin }^2\frac{\pi }{2}.\cos \frac{\pi }{2}=\pi$.

Bài 9.20 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = $\frac{1}{3}{x}^3-x^2-3x+1$ . Tập nghiệm của bất phương trình f'(x) ≤ 0 là

A. [1; 3].

B. [–1; 3].

C. [–3; 1].

D. [–3; –1].

Lời giải:

Đáp án đúng là: B

Ta có f'(x) = x² – 2x – 3.

Khi đó f'(x) ≤ 0 ⇔ x² – 2x – 3 ≤ 0 ⇔ –1 ≤ x ≤ 3.

Bài 9.21 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = $\sqrt{4+3u\left(x\right)}$ với u(1) = 7, u'(1) = 10. Khi đó f'(1) bằng

A. 1.

B. 6.

C. 3.

D. –3.

Lời giải:

Đáp án đúng là: C

Ta có f'(x) = $\frac{3u^{\text{'}}\left(x\right)}{2\sqrt{4+3u\left(x\right)}}$.

Nên f'(1) = $\frac{3u^{\text{'}}\left(1\right)}{2\sqrt{4+3u\left(1\right)}}=\frac{3.10}{2\sqrt{4+3.7}}=3$ .

Bài 9.22 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = x²e^–2x. Tập nghiệm của phương trình f'(x) = 0 là

A. {0; 1}.

B. {–1; 0}.

C. {0}.

D. {1}.

Lời giải:

Đáp án đúng là: A

Ta có f'(x) = (x²)' . e^{– 2x} + x² . (e^{– 2x})' = 2xe^–2x – 2x²e^–2x.

Để f'(x) = 0 ⇔ 2xe^–2x – 2x²e^–2x = 0

⇔ 2xe^–2x(1 – x) = 0

Bài 9.23 trang 97 Toán 11 Tập 2: Chuyển động của một vật có phương trình s(t) = sin$\left(0,8\pi t+\frac{\pi }{3}\right)$, ở đó s tính bằng centimét và thời gian t tính bằng giây. Tại các thời điểm vận tốc bằng 0, giá trị tuyệt đối của gia tốc của vật gần với giá trị nào sau đây nhất?

A. 4,5 cm/s².

B. 5,5 cm/s².

C. 6,3 cm/s².

D. 7,1 cm/s².

Lời giải:

Đáp án đúng là: C

Ta có: v(t) = s'(t) = 0,8πcos$\left(0,8\pi t+\frac{\pi }{3}\right)$;

a(t) = s''(t) = –0,8π.0,8πsin$\left(0,8\pi t+\frac{\pi }{3}\right)$ = –0,64π²sin$\left(0,8\pi t+\frac{\pi }{3}\right)$ .

Ta có v(t) = 0

$\iff 0,8\pi \cos \left(0,8\pi t+\frac{\pi }{3}\right)=0$

$\iff 0,8\pi t+\frac{\pi }{3}=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff 0,8\pi t=\frac{\pi }{2}-\frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff t=\frac{5}{24}+\frac{5k}{4}\left(k\in \mathbb{Z}\right)$

Thời điểm vận tốc bằng 0 giá trị tuyệt đối của gia tốc của vật là:

$=0,64{\pi }^2$$=0,64{\pi }^2\approx 6,32$.

Bài 9.24 trang 97 Toán 11 Tập 2: Cho hàm số y = x³ – 3x² + 4x – 1 có đồ thị là (C). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm M trên đồ thị (C) là

A. 1.

B. 2.

C. –1.

D. 3.

Lời giải:

Đáp án đúng là: A

Hệ số góc của tiếp tuyến tại một điểm M trên đồ thị (C) là

k = y' = 3x² – 6x + 4 = 3(x² – 2x + 1) + 1 = 3(x – 1)² + 1 ≥ 1 với mọi x.

Vậy hệ số góc nhỏ nhất của tiếp tuyến tại một điểm M trên đồ thị (C) là 1.

Bài 9.25 trang 97 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) $y={\left(\frac{2x-1}{x+2}\right)}^5$ ;

b) $y=\frac{2x}{x^2+1}$ ;

c) y = e^xsin²x;

d) y = log(x+$\sqrt{x}$).

Lời giải:

a) Với x ≠ – 2, ta có

$y^{\text{'}}=5{\left(\frac{2x-1}{x+2}\right)}^4.{\left(\frac{2x-1}{x+2}\right)}^{\text{'}}=5{\left(\frac{2x-1}{x+2}\right)}^4.\frac{2\left(x+2\right)-\left(2x-1\right)}{{\left(x+2\right)}^2}$

$=5{\left(\frac{2x-1}{x+2}\right)}^4.\frac{5}{{\left(x+2\right)}^2}=\frac{25{\left(2x-1\right)}^4}{{\left(x+2\right)}^6}$.

b) Ta có

$y^{\text{'}}=\frac{{\left(2x\right)}^{\text{'}}.\left(x^2+1\right)-2x{\left(x^2+1\right)}^{\text{'}}}{{\left(x^2+1\right)}^2}=\frac{2x^2+2-4x^2}{{\left(x^2+1\right)}^2}=\frac{-2x^2+2}{{\left(x^2+1\right)}^2}$.

c) Ta có

y' = (e^x)' . sin²x + e^x(sin²x)' = e^xsin²x + e^x.2sinx.cosx = e^xsin²x + e^xsin2x.

d) Với x > 0, ta có:

$y^{\text{'}}=\frac{{\left(x+\sqrt{x}\right)}^{\text{'}}}{\left(x+\sqrt{x}\right)\ln 10}=\frac{1+\frac{1}{2\sqrt{x}}}{\left(x+\sqrt{x}\right)\ln 10}=\frac{2\sqrt{x}+1}{2\sqrt{x}\left(x+\sqrt{x}\right)\ln 10}$.

Giải Toán 11 trang 98 Tập 2

Bài 9.26 trang 98 Toán 11 Tập 2: Xét hàm số lũy thừa y = x^α với α là số thực.

a) Tìm tập xác định của hàm số đã cho.

b) Bằng cách viết y = x^α = e^αlnx, tính đạo hàm của hàm số đã cho.

Lời giải:

a)

Hàm số lũy thừa y = x^α với α là số thực có tập xác định khác nhau, phụ thuộc vào α:

+ Nếu α nguyên dương thì tập xác định là ℝ.

+ Nếu α nguyên âm hoặc α = 0 thì tập xác định là ℝ\{0}.

+ Nếu α không nguyên thì tập xác định là (0; +∞).

b) Ta có

y' = (x^α)' = (e^αlnx)' = (α.lnx)' e^αlnx = $\frac{\alpha }{x}{e}^{\alpha \ln x}=\frac{\alpha }{x}.x^{\alpha }$ = αx^α–1.

Bài 9.27 trang 98 Toán 11 Tập 2: Cho hàm số f(x) = $\sqrt{3x+1}$ . Đặt g(x) = f(1) + 4(x² – 1).f'(1). Tính g(2).

Lời giải:

Với x>-$\frac{1}{3}$, ta có: f'(x) = $\frac{{\left(3x+1\right)}^{\text{'}}}{2\sqrt{3x+1}}=\frac{3}{2\sqrt{3x+1}}$ .

Do đó, f(1) = $\sqrt{3.1+1}$ = 2, f'(1) = $\frac{3}{2\sqrt{3.1+1}}$ = $\frac{3}{4}$ .

Vậy g(2) = f(1) + 4(2² – 1).f'(1) = 2 + 12.$\frac{3}{4}$ = 11.

Bài 9.28 trang 98 Toán 11 Tập 2: Cho hàm số f(x) = $\frac{x+1}{x-1}$ . Tính f''(0).

Lời giải:

Với x ≠ 1, ta có $f^{\text{'}}\left(x\right)=\frac{{\left(x+1\right)}^{\text{'}}.\left(x-1\right)-\left(x+1\right).{\left(x-1\right)}^{\text{'}}}{{\left(x-1\right)}^2}=\frac{-2}{{\left(x-1\right)}^2}$ ;

${f^{\text{'}}}^{\text{'}}\left(x\right)=\left(-2\right).\frac{-2\left(x-1\right).{\left(x-1\right)}^{\text{'}}}{{\left(x-1\right)}^4}=\frac{4}{{\left(x-1\right)}^3}$.

Khi đó, ${f^{\text{'}}}^{\text{'}}\left(0\right)=\frac{4}{{\left(0-1\right)}^3}=-4$ .

Bài 9.29 trang 98 Toán 11 Tập 2: Cho hàm số f(x) thỏa mãn f(1) = 2 và f'(x) = x²f(x) với mọi x. Tính f''(1).

Lời giải:

Ta có f''(x) = (x²)' . f(x) + x² . f'(x) = 2xf(x) + x²f'(x).

Vì f(1) = 2 nên f'(1) = 1² . f(1) = 1 . 2 = 2.

Suy ra f''(1) = 2 . 1 . f(1) + 1² . f'(1) = 2 . 2 + 2 = 6.

Bài 9.30 trang 98 Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số y = x³ + 3x² – 1 tại điểm có hoành độ bằng 1.

Lời giải:

Ta có: y' = 3x² + 6x ⇒ y'(1) = 3 . 1² + 6 . 1 = 9.

Ngoài ra, f(1) = 1³ + 3 . 1² – 1 = 3 nên phương trình tiếp tuyến cần tìm là:

y – 3 = 9(x – 1) hay y = 9x – 6.

Bài 9.31 trang 98 Toán 11 Tập 2: Đồ thị của hàm số y = $\frac{a}{x}$ (a là hằng số dương) là một đường hypebol. Chứng minh rằng tiếp tuyến tại một điểm bất kì của đường hypebol đó tạo với các trục tọa độ một tam giác có diện tích không đổi.

Lời giải:

Ta có: $y^{\text{'}}=\frac{-a}{x^2}$ .

Phương trình tiếp tuyến của hypebol tại điểm có hoành độ x₀ (x₀ ≠ 0) là

$y-\frac{a}{x_0}=\frac{-a}{{x_0}^2}\left(x-x_0\right)hayy=\frac{-a}{{x_0}^2}x+\frac{2a}{x_0}$.

Giả sử phương trình tiếp tuyến này cắt hai trục tọa độ lần lượt tại A, B.

Khi đó, $A\left(0;\frac{2a}{x_0}\right),B\left(2x_0;0\right)$ .

Do đó diện tích tam giác OAB bằng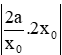: $\frac{1}{2}$OA.OB = $\frac{1}{2}$ = 2a không đổi (do a là hằng số dương).

Vậy tiếp tuyến tại một điểm bất kì của đường hypebol đó tạo với các trục toạ độ một tam giác có diện tích không đổi.

Bài 9.32 trang 98 Toán 11 Tập 2: Hình 9.10 biểu diễn đồ thị của ba hàm số. Hàm số thứ nhất là hàm vị trí của một chiếc ô tô, hàm số thứ hai biểu thị vận tốc và hàm số thứ ba biểu thị gia tốc của ô tô đó. Hãy xác định đồ thị của mỗi hàm số này và giải thích.

Lời giải:

Từ ý nghĩa cơ học của đạo hàm, ta biết rằng đạo hàm của hàm vị trí là hàm vận tốc, đạo hàm của hàm vận tốc là hàm gia tốc và một hàm số đồng biến (tương ứng nghịch biến) trên một khoảng nào đó nếu đạo hàm của nó dương (tương ứng âm) trên khoảng đó.

Từ hình vẽ ta thấy: Hàm số c luôn đồng biến, tức là đạo hàm của nó phải luôn không âm, do đó hàm số b là đạo hàm của hàm số c; hàm số b đồng biến trên khoảng mà hàm số a dương và nghịch biến trên khoảng mà hàm số a âm, do đó hàm số a là đạo hàm của hàm số b.

Vậy hàm số a là hàm gia tốc, hàm số b là hàm vận tốc và hàm số c là hàm vị trí của ô tô.

Bài 9.33 trang 98 Toán 11 Tập 2: Vị trí của một vật chuyển động thẳng được cho bởi phương trình: s = f(t) = t³ – 6t² + 9t, trong đó t tính bằng giây và s tính bằng mét.

a) Tính vận tốc của vật tại các thời điểm t = 2 giây và t = 4 giây.

b) Tại những thời điểm nào vật đứng yên?

c) Tìm gia tốc của vật tại thời điểm t = 4 giây.

d) Tính tổng quãng đường vật đi được trong 5 giây đầu tiên.

e) Trong 5 giây đầu tiên, khi nào vật tăng tốc, khi nào vật giảm tốc?

Lời giải:

a) Ta có: v(t) = s'(t) = 3t² – 12t + 9.

Vận tốc của vật tại thời điểm t = 2 giây là v(2) = 3 . 2² – 12 . 2 + 9 = –3 (m/s).

Vận tốc của vật tại thời điểm t = 4 giây là v(4) = 3 . 4² – 12 . 4 + 9 = 9 (m/s).

b) Khi vật đứng yên ta có: v(t) = 0 ⇔ 3t² – 12t + 9 = 0 ⇔ t = 1 hoặc t = 3.

Vậy tại thời điểm 1 giây hoặc 3 giây thì vật đứng yên.

c) Ta có: a(t) = s''(t) = 6t – 12.

Gia tốc của vật tại thời điểm t = 4 giây là a(4) = 6 . 4 – 12 = 12 (m/s²).

d) Ta có khi t = 1 hoặc t = 3 thì vật đứng yên.

Do đó, ta cần tính riêng rẽ quãng đường vật đi được trong từng khoảng thời gian [0; 1], [1; 3], [3; 5].

Ta có: f(0) = 0³ – 6 . 0² + 9 . 0 = 0; f(1) = 1³ – 6 . 1² + 9 . 1 = 4;

f(3) = 3³ – 6 . 3² + 9 . 3 = 0; f(5) = 5³ – 6 . 5² + 9 . 5 = 20.

Từ thời điểm t = 0 giây đến thời điểm t = 1 giây, vật đi được quãng đường là:

|f(1) – f(0)| = |4 – 0| = 4 (m).

Từ thời điểm t = 1 giây đến thời điểm t = 3 giây, vật đi được quãng đường là:

|f(3) – f(1)| = |0 – 4| = 4 (m).

Từ thời điểm t = 3 giây đến thời điểm t = 5 giây, vật đi được quãng đường là:

|f(5) – f(3)| = |20 – 0| = 20 (m).

Tổng quãng đường vật đi được trong 5 giây đầu tiên là 4 + 4 + 20 = 28 (m).

e)

Xét a(t) = 0, tức là 6t – 12 = 0 ⇔ t = 2.

Với t ∈ [0; 2) thì gia tốc âm, tức là vật giảm tốc.

Với t ∈ (2; 5] thì gia tốc dương, tức là vật tăng tốc.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: