Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 33: Đạo hàm cấp hai chi tiết sách Toán 11 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 33: Đạo hàm cấp hai

Giải Toán 11 trang 95 Tập 2

Mở đầu trang 95 Toán 11 Tập 2: Chuyển động của một vật gắn trên con lắc lò xo (khi bỏ qua ma sát và sức cản không khí) được cho bởi phương trình sau:

x(t) = 4cos$\left(2\pi t+\frac{\pi }{3}\right)$,

ở đó x tính bằng centimet và thời gian t tính bằng giây. Tìm gia tốc tức thời của vật tại thời điểm t = 5 giây (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Vận tốc của vật tại thời điểm t là

v(t) = x'(t) = -$\left(2\pi t+\frac{\pi }{3}\right)$'.4sin$\left(2\pi t+\frac{\pi }{3}\right)$ = -8$\pi$sin$\left(2\pi t+\frac{\pi }{3}\right)$.

Gia tốc tức thời của vật tại thời điểm t là:

a(t) = v'(t) = -8$\pi$$\left(2\pi t+\frac{\pi }{3}\right)$'.cos$\left(2\pi t+\frac{\pi }{3}\right)$ = -16${\pi }^2$cos$\left(2\pi t+\frac{\pi }{3}\right)$.

Tại thời điểm t = 5, gia tốc của vật là:

a(5) = $-16{\pi }^2\cos \left(2\pi .5+\frac{\pi }{3}\right)\approx -79$ (cm/s²).

1. Khái niệm đạo hàm cấp hai

HĐ1 trang 95 Toán 11 Tập 2: Nhận biết đạo hàm cấp hai của một hàm số

a) Gọi g(x) là đạo hàm của hàm số y = sin$\left(2x+\frac{\pi }{4}\right)$. Tìm g(x).

b) Tính đạo hàm của hàm số y = g(x).

Lời giải:

a) Ta có

g(x) = y' = 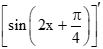= 2.cos$\left(2x+\frac{\pi }{4}\right)$.

b) Ta có

g'(x) =  = -4sin$\left(2x+\frac{\pi }{4}\right)$.

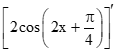
Luyện tập 1 trang 95 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = xe^2x;

b) y = ln(2x + 3).

Lời giải:

a) Ta có y = xe^2x

Suy ra: y' = x' . e^2x + x . (e^2x)' = e^2x + 2xe^2x.

Do đó, y'' = 2e^2x + 2(e^2x + 2xe^2x) = 2e^2x + 2e^2x + 4xe^2x = 4e^2x + 4xe^2x.

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = 4e^2x + 4xe^2x.

b) Ta có y = ln(2x + 3).

y' = $\frac{(2x+3{)}^{\text{'}}}{2x+3}=\frac{2}{2x+3}$ .

y'' = ${\left(\frac{2}{2x+3}\right)}^{\text{'}}=\frac{-2.2}{{\left(2x+3\right)}^2}=\frac{-4}{{\left(2x+3\right)}^2}$ .

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = $\frac{-4}{{\left(2x+3\right)}^2}$ .

2. Ý nghĩa cơ học của đạo hàm cấp hai

Giải Toán 11 trang 96 Tập 2

HĐ2 trang 96 Toán 11 Tập 2: Nhận biết ý nghĩa cơ học của đạo hàm cấp hai

Xét một chuyển động có phương trình s = 4cos2πt.

a) Tính vận tốc tức thời của chuyển động tại thời điểm t.

b) Tính gia tốc tức thời tại thời điểm t.

Lời giải:

a)

Ta có: v(t) = s'(t) = –4.2πsin2πt = –8πsin2πt.

Vậy vận tốc tức thời của chuyển động tại thời điểm t là –8πsin2πt.

b) Gia tốc tức thời tại thời điểm t là

a(t) = v'(t) = (–8πsin2πt)' = –8π.2πcos2πt = –16π²cos2πt.

Vận dụng trang 96 Toán 11 Tập 2: Một chuyển động thẳng có phương trình $s=2t^2+\frac{1}{2}{t}^4$ (s tính bằng mét, t tính bằng giây). Tìm gia tốc của vật tại thời điểm t = 4 giây.

Lời giải:

Vận tốc tại thời điểm t là v(t) = s'(t) = 4t + 2t³.

Gia tốc tức thời của vật tại thời điểm t là a(t) = v'(t) = 4 + 6t².

Tại thời điểm t = 4 giây, gia tốc của vật là:

a(4) = 4 + 6 . 4² = 100 (m/s²).

Bài tập

Bài 9.13 trang 96 Toán 11 Tập 2: Cho hàm số f(x) = x²e^x. Tính f''(0).

Lời giải:

Với f(x) = x²e^x, ta có:

f'(x) = (x²)' . e^x + x² . (e^x)' = 2x.e^x + x².e^x.

f''(x) = (2e^x + 2x.e^x) + (2x.e^x + x².e^x) = 4xe^x + 2e^x + x²e^x.

Vậy f''(0) = 4 . 0 . e⁰ + 2 . e⁰ + 0² . e⁰ = 2.

Bài 9.14 trang 96 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = ln(x + 1);

b) y = tan2x.

Lời giải:

a) Ta có y' = (ln(x+1))' = $\frac{{\left(x+1\right)}^{\text{'}}}{x+1}=\frac{1}{x+1}$

$\Rightarrow {y^{\text{'}}}^{\text{'}}={\left(\frac{1}{x+1}\right)}^{\text{'}}=\frac{-1}{{\left(x+1\right)}^2}$.

b)

Ta có y' = (tan2x)' = $\frac{2}{{\cos }^{2}2x}$

$\Rightarrow {y^{\text{'}}}^{\text{'}}=\frac{-2{\left({\cos }^{2}2x\right)}^{\text{'}}}{{\cos }^{4}2x}=\frac{-2.2\cos 2x.(\cos 2x{)}^{\text{'}}}{{\cos }^{4}2x}$

$=\frac{4.2\sin 2x}{{\cos }^{3}2x}=\frac{8\sin 2x}{{\cos }^{3}2x}$.

Bài 9.15 trang 96 Toán 11 Tập 2: Cho hàm số P(x) = ax² + bx + 3 (a, b là hằng số). Tìm a, b biết P'(1) = 0 và P''(1) = –2.

Lời giải:

Ta có:

P'(x) = 2ax + b

P''(x) = 2a

Do P'(1) = 0 và P''(1) = –2 nên ta có

Vậy a = – 1 và b = 2.

Bài 9.16 trang 96 Toán 11 Tập 2: Cho hàm số f(x) = $2{\sin }^2\left(x+\frac{\pi }{4}\right)$ . Chứng minh rằng |f''(x)| ≤ 4 với mọi x.

Lời giải:

Ta có:

$f^{\text{'}}\left(x\right)=2.2\sin \left(x+\frac{\pi }{4}\right)$.

$=4\sin \left(x+\frac{\pi }{4}\right)\cos \left(x+\frac{\pi }{4}\right)=2\sin \left(2x+\frac{\pi }{2}\right)$

Khi đó ${f^{\text{'}}}^{\text{'}}\left(x\right)=2.{\left(2x+\frac{\pi }{2}\right)}^{\text{'}}.\cos \left(2x+\frac{\pi }{2}\right)=4\cos \left(2x+\frac{\pi }{2}\right)$ .

Vì  với mọi x nên 4 $\le$4 với mọi x.

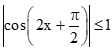
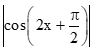
Vậy |f''(x)| ≤ 4 với mọi x.

Bài 9.17 trang 96 Toán 11 Tập 2: Phương trình chuyển động của một hạt được cho bởi s(t) = 10 + 0,5sin$\left(2\pi t+\frac{\pi }{5}\right)$, trong đó s tính bằng centimet và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Vận tốc tại thời điểm t là:

v(t) = s'(t) = 0,5.2πcos$\left(2\pi t+\frac{\pi }{5}\right)$= πcos$\left(2\pi t+\frac{\pi }{5}\right)$.

Gia tốc tức thời của vật tại thời điểm t là:

a(t) = v'(t) = –π.2πsin$\left(2\pi t+\frac{\pi }{5}\right)$= –2π²sin$\left(2\pi t+\frac{\pi }{5}\right)$.

Tại thời điểm t = 5 giây, gia tốc của vật là:

a(5) = –2π²sin$\left(2\pi t+\frac{\pi }{5}\right)$ ≈ –11,6 (cm/s²).

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: