Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 8 Bài 2: Các trường hợp đồng dạng của hai tam giác sách Chân trời sáng tạo. Bài viết gồm 53 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 8.
Trắc nghiệm Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác
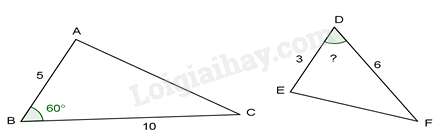
Câu 1 : Cho hai tam giác ABC và MNP có kích thước như trong hình, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng là bao nhiêu?
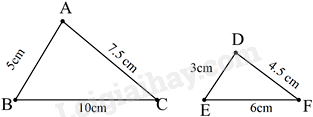
Đáp án : D
Vì ABDE=53;ACDF=7,54,5=53;BCEF=106=53
Suy ra: ABDE=ACDF=BCEF=53⇒ΔABC∽ΔDEF với tỉ số đồng dạng là 53
Tỉ số của các cạnh tương ứng là tỉ số đồng dạng của hai tam giác.
Câu 2 : Cho hình vẽ sau, hãy cho biết hai tam giác nào đồng dạng?
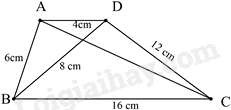
Đáp án : B
Vì ADDB=48=12;ABDC=612=12;BDBC=816=12
Suy ra: ADDB=ABDC=DBBC=12⇒ΔADB∽ΔDBC (Trường hợp đồng dạng thứ nhất),
Câu 3 : Cho tam giác ABC có AB = 3cm; AC = 6cm; BC = 9cm và MNP có MN = 1cm; MP = 2cm; NP = 3cm. Tỉ số chu vi của hai tam giác MNP và ABC là
Đáp án : C
Vì MNAB=13;MPAC=26=13;NPBC=39=13
Suy ra: MNAB=MPAC=NPBC=13⇒ΔMNP∽ΔABC theo tỉ số đồng dạng 13 .
Vì MNAB=MPAC=NPBC=MN+MP+NPAB+AC+BC=13⇒CVΔMNPCVΔABC=13
Câu 4 : Cho tam giác ABC có AB = 12cm, AC = 8cm, BC = 6cm. Tam giác MNP đồng dạng với tam giác ABC và có chu vi bằng 52. Độ dài các cạnh của tam giác MNP là:
Đáp án : B
Vì ΔMNP∽ΔABC
⇒MNAB=MPAC=NPBC=MN+MP+NPAB+AC+BC=5212+8+6=5226=2⇒MN12=MP8=NP6=2⇒MN=2.12=24(cm);MP=2.8=16(cm);NP=2.6=12(cm)
Câu 5 : Cho ΔABC∽ΔA1B1C1 khẳng định nào sau đây là sai
Đáp án : D
ΔABC∽ΔA1B1C1 ⇒ABA1B1=ACA1C1=BCB1C1 (các cạnh tương ứng)
⇒A1B1AB=A1C1AC=B1C1BC (Tính chất tỉ lệ thức)
⇒B1C1BC=A1C1AC=A1B1AB (Tính chất tỉ lệ thức)
⇒ABA1B1=A1C1AC=BCB1C1 là khẳng định sai
Câu 6 : Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :
Đáp án : B
Vì 38=618(=12)≠415 nên hai tam giác có độ dài các cạnh 3cm; 4cm; 6cm và 9 cm; 15cm; 18 cm không đồng dạng với nhau
Vì 48=510=612 nên hai tam giác có độ dài các cạnh là 4cm; 5cm; 6cm và 8cm; 10cm; 12cm đồng dạng với nhau theo trường hợp thứ nhất. Chọn B
Vì 63=63≠55 nên hai tam giác có độ dài các cạnh là 6cm; 5 cm; 6 cm và 3cm; 5cm; 3 cm không đồng dạng với nhau.
Vì 510=714≠1018 nên hai tam giác có độ dài các cạnh là 5cm; 7cm; 1 dm và 10cm; 14cm; 18 cm không đồng dạng với nhau.
Câu 7 : Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?
Đáp án : C
Vì ABNP=68=34;ACNM=912=34;BCPM=1216=34
Nên ABNP=ACNM=BCPM=34⇒ΔABC∽ΔNPM
Câu 8: Với điều kiện nào sau đây thì ΔABC∽ΔMNP
Đáp án : A
ABMN=ACMP=BCNP⇒ΔABC∽ΔMNP
Câu 9 : Cho ΔABC∽ΔMNP biết AB=3cm;BC=4cm;MN=6cm;MP=5cm . Khi đó:
Đáp án : B
ΔABC∽ΔMNP⇒ABMN=ACMP=BCNP⇒36=AC5=4NP⇒AC=3.56=2,5(cm)⇒NP=4.63=8(cm)
Vậy AC = 2,5cm; NP = 8cm
Câu 10 : Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm;
MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là
Đáp án : D
Vì ABMN=36=12;ACMP=510=12;BCNP=714=12
Suy ra: ABMN=ACMP=BCNP=12⇒ΔABC∽ΔMNP theo tỉ số đồng dạng là 12
Vì ABMN=ACMP=BCNP=AB+AC+BCMN+MP+NP=12
⇒CVΔABCCVΔMNP=12
Câu 11 : Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với 4:5:6 . Cho biết ΔABC∽ΔA′B′C′ và cạnh nhỏ nhất của ΔA′B′C′ bằng 2cm. Độ dài các cạnh còn lại của tam giác A′B′C′ lần lượt là
Đáp án : D
Theo đầu bài tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với 4:5:6
Và ΔABC∽ΔA′B′C′ nên ΔA′B′C′ cũng có độ dài các cạnh tỉ lệ với 4:5:6
Giả sử A′B′<A′C′<B′C′⇒A′B′=2cm
⇒A′B′4=A′C′5=B′C′6⇒A′C′5=B′C′6=24
⇒A′C′=5.24=2,5(cm)⇒B′C′=6.24=3(cm)
Độ dài các cạnh còn lại của tam giác A’B’C’ lần lượt là 2,5cm ; 3cm.
Câu 12 : Cho tam giác ABC có AB= 16cm; AC = 18cm; BC = 25cm. Cho biết ΔABC∽ΔA′B′C′ và AB – A’B’= 8cm. Độ dài các cạnh của tam giác A’B’C’ là:
Đáp án : A
Theo đầu bài ΔABC∽ΔA′B′C′ nên ⇒ABA′B′=ACA′C′=BCB′C′ (các cạnh tương ứng)
⇒ABAB−A′B′=ACAC−A′C′=BCBC−B′C′⇒168=1616−A′B′=1818−A′C′=2525−B′C′=2⇒1616−A′B′=2⇒16−A′B′=8⇒A′B′=8(cm)⇒1818−A′C′=2⇒18−A′C′=9⇒A′C′=9(cm)⇒2525−B′C′=2⇒25−B′C′=252⇒B′C′=12,5(cm)
Độ dài các cạnh còn lại của tam giác A’B’C’ là: A’B’ = 8cm; A’C’ = 9cm; B’C’ = 12,5cm
Câu 13 : Tam giác thứ nhất có cạnh nhỏ nhất bằng 8cm, hai cạnh còn lại bằng x và y (x < y). Tam giác thứ hai có cạnh lớn nhất bằng 27cm hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đồng dạng:
Đáp án : A
Theo đề bài:
Tam giác thứ nhất có cạnh lần lượt là 8; x; y (8 < x < y)
Tam giác thứ hai có cạnh lần lượt là x; y ; 27 ( x < y < 27)
Để hai tam giác đồng dạng cần:
8x=xy=y27⇒xy=8.27;x2=8y⇒y=8.27x;x2=8.8.27x⇒x3=64.27=(4.3)3
Vậy x = 12cm; y = 18cm
Câu 14 : Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Cho biết tam giác ABC có chu vi bằng 450cm, chu vi tam giác PQR có độ dài là
Đáp án : C
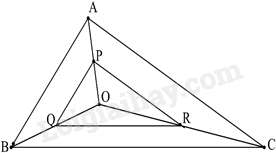
Vì P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Nên PQ, QR, RP lần lượt là đường trung bình của các tam giác AOB; BOC; AOC. Nên ta có:
PQAB=QRBC=PRAC=12
Suy ra: ΔPQR∽ΔABC
Vì:
PQAB=QRBC=PRAC=PQ+QR+PRAB+BC+AC=CVΔPQRCVΔABC⇒CVΔPQRCVΔABC=12⇒CVΔPQR=CVΔABC2=4502=225(cm)
Câu 15 : Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm và tam giác A’B’C’ vuông tại A’ có A’B’= 3cm; A’C’ = 4cm. Tam giác ABC đồng dạng với tam giác A’B’C’ không và nếu có thì tỉ số chu vi của hai tam giác là bao nhiêu?
Đáp án : A
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
AB2+AC2=BC2⇒BC2=62+82=100⇒BC=10(cm)
Áp dụng định lý Pythagore vào tam giác A’B’C’ vuông tại A’ ta có:
A′B′2+A′C′2=B′C′2⇒B′C′2=32+42=25⇒B′C′=5(cm)
Ta thấy: ABA′B′=63=2;ACA′C′=84=2;BCB′C′=105=2
⇒ABA′B′=ACA′C′=BCB′C′=AB+AC+BCA′B′+A′C′+B′C′=CVΔABCCVΔA′B′C′=2
Vì ΔABC∽ΔA′B′C′ tỉ số chu vi của hai tam giác là 2.
Câu 16 : Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
Đáp án : D
Hai tam giác đồng dạng với nhau theo trường hợp cạnh - góc – cạnh nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Câu 17 : Cho ΔDEF và ΔILK , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để ΔDEF∽ΔILK(c−g−c)?
Đáp án : B
Ta có: DEIL=EFLK(1020=48=12).
Để ΔDEF∽ΔILK(c−g−c) thì ˆE=ˆL (hai góc tạo bởi các cặp cạnh)
Câu 18 : Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây.
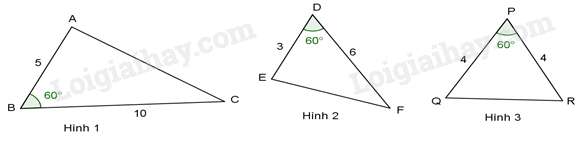
Đáp án : A
Ta có: BABC=510=12,DEDF=36=12,PQPR=44=1 ,
Xét ΔABC và ΔEDF ta có: BABC=DEDF=12⇔BADE=BCDF và ˆB=ˆD=600(gt)
⇒ΔABC∽ΔEDF(c−g−c)
Hình 1 và hình 2 là hai tam giác đồng dạng
Câu 19 : Để hai tam giác ABC và DEF đồng dạng thì số đo ˆD trong hình vẽ dưới bằng
Đáp án : B
Ta có: BABC=510=12,DEDF=36=12
⇒BABC=DEDF=12⇔BADE=BCDF
Để hai tam giác đã cho đồng dạng thì ˆB=ˆD=600 .
Câu 20 : Cho ΔA′B′C′ và ΔABC có ˆA=ˆA′ . Để ΔA′BC′∽ΔABC cần thêm điều kiện là:
A′B′AB=A′C′AC.
A′B′AB=B′C′BC.
A′B′AB=BCB′C′.
B′C′BC=ACA′C′.
Đáp án : A
Ta có: ˆA=^A′ và A′B′AB=A′C′AC thì ΔA′B′C′∽ΔABC (c-g-c)
Câu 21 : Cho ΔABC và ΔDEF có ˆB=ˆE , BABC=DEEF thì:
Đáp án : A
ΔABC và ΔDEF có ˆB=ˆE , BABC=DEEF thì ΔABC∽ΔDEF(c−g−c).
Câu 22 : Cho ΔMNP∽ΔKIH , biết ˆM=ˆK,MN=2cm,MP=8cm,KH=4cm , thì KI bằng bao nhiêu:
Đáp án : D
ΔMNP∽ΔKIH⇒MNKI=MPKH⇔2KI=84⇒KI=1(cm)
Câu 23 : Hãy chọn câu đúng. Nếu ΔABC và ΔDEF có ˆB=ˆE , BADE=BCEF thì
Đáp án : C
ΔABC và ΔDEF có ˆB=ˆE , BADE=BCEF thì ΔABC∽ΔDEF.
Câu 24 : Cho ΔABC , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho ADAB=AEAC. Kết luận nào sau đây sai:
Đáp án : C
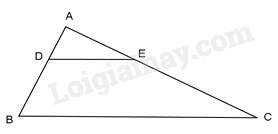
Xét ΔADE và ΔABC ta có: ADAB=AEAC. (gt); ˆA chung
⇒ΔADE∽ΔABC(c−g−c)
⇒^ADE=^ABC (cặp góc tương ứng)
\Rightarrow \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = & \frac{{DE}}{{BC}}
⇒DE//BC (định lý Ta lét đảo)
Câu 25 : Cho ΔABC , có AC = 18cm; AB = 9cm; BC = 15cm. Trên cạnh AC lấy điểm N sao cho AN = 3cm, trên cạnh AB lấy điểm M sao cho AM = 6cm. Tính độ dài đoạn thẳng MN:
Đáp án : B
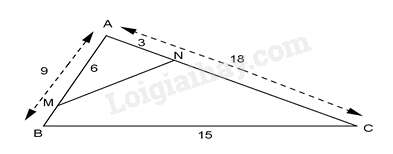
Ta có: ANAB=39=13,AMAC=618=13⇒ANAB=AMAC=13
Xét ΔANM và ΔABC có: ANAB=AMAC(cmt);ˆA chung
⇒ΔANM∽ΔABC(c−g−c)⇒ANAB=AMAC=MNCB=13⇒MN15=13⇒MN=153=5(cm).
Câu 26 : Với AB//CD thì giá trị của x trong hình vẽ dưới đây là
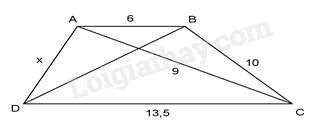
Đáp án : A
Ta có ABAC=69=23,ACCD=913,5=23
⇒ABAC=ACCD=23
Xét ΔABC và ΔCAD có: ABAC=ACCD(cmt),^BAC=^ACD (so le trong, AB//CD )
⇒ΔABC∽ΔCAD(c−g−c)⇒ABAC=CACD=BCAD=23⇒10x=23⇒x=10.32=15
Câu 27 : Cho ΔABC vuông tại A, đường cao AH(H∈BC) . Biết AB = 3cm, AC = 6cm,
AH = 2cm, HC = 4cm. Hệ thức nào sau đây đúng:
Đáp án : C
Xét ΔABC và ΔHAC có: ABAC=36=12,AHHC=24=12
⇒ABAC=AHHC=12⇒AB.HC=AH.AC
Câu 28 : Cho hình thang vuông ABCD(ˆA=ˆD=900) có AB = 16cm, CD = 25cm,
BD = 20cm. Độ dài cạnh BC là:
Đáp án : C
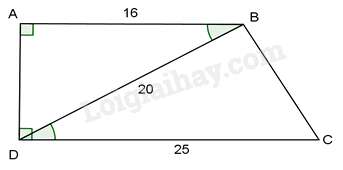
ΔABD và ΔBDC có: ^ABD=^BDC (so le trong, AB//CD)
ABBD=BDDC (Vì 1620=2025)
Do đó ΔABD∽ΔBDC(c−g−c)
Ta có ˆA=900 nên ^DBC=900 . Theo định lí Pytago, ta có:
BC2=CD2−BD2=252−202=152 .Vậy BC= 15 (cm)
Câu 29 : Cho ΔMNP∽ΔEFH theo tỉ số k. Gọi MM′,EE′ lần lượt là hai trung tuyến của ΔMNP và ΔEFH . Khi đó ta chứng minh được:
EE′MM′=k
MM′EE′=k
MM′EE′=k2
EE′MM′=k2
Đáp án : B
Ta có tỉ số đồng dạng bằng với tỉ số đường trung tuyến tương ứng MM′EE′=k
Tỉ số đồng dạng bằng với tỉ số đường trung tuyến tương ứng.
Câu 30 : Cho tam giác nhọn ABC có ˆC=600 . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
Đáp án : B
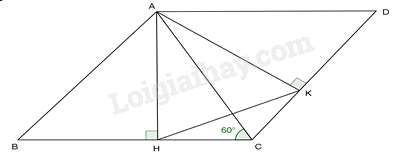
Vì AD.AH=AB.AK(=SABCD) nên AHAK=ABAD=ABBC
Ta lại có AB//CD (vì ABCD là hình bình hành) mà AK⊥DC⇔AK⊥AB⇒^BAK=900
Từ đó ^HAK=^ABC (cùng phụ với ^BAH )
Nên ΔAKH∽ΔBCA(c−g−c)⇒^AKH=^ACB=600
Câu 31 : Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc B bằng bao nhiêu lần góc A?
Đáp án : C
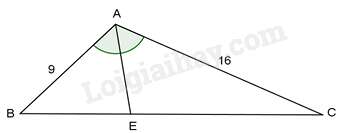
Kẻ đường phân giác AE của ΔABC . Theo tính chất đường phân giác, ta có:
BEEC=ABAC=916
Nên BE+ECEC=9+1616
Hay 20EC=2516⇒EC=12,8(cm)
Xét ΔACB và ΔECA có: ˆC là góc chung
ACEC=CBCA (vì 1612,8=2016)
Do đó ΔACB∽ΔECA (c-g-c) suy ra ˆB=^CAE tức là ˆB=ˆA2
Câu 32 : Cho hình thoi ABCD cạnh a, có ˆA=600 . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính ^BKD .
Đáp án : C
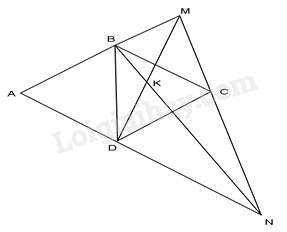
Do BC//AN (Vì N∈AD ) nên ta có: MBAB=MCNC (1)
Do CD//AM (Vì M∈AB ) nên ta có: MCNC=ADDN (2)
Từ (1) và (2) ⇒MBAB=ADDN
ΔABD có AB = AD (định nghĩa hình thoi) và ˆA=600 nên ΔABD là tam giác đều
⇒AB=BD=DA
Từ ⇒MBAB=ADDN(cmt)⇒MBBD=BDDN
Mặt khác ^MBD=^DBN=1200
Xét ΔMBD và ΔBDN có: MBBD=BDDN,^MBD=^DBN
⇒ΔMBD∽ΔBDN(c−g−c)⇒^BMD=^DBN
Xét ΔMBD và ΔKBD có: ^MBD=^DBN,^BDM chung
⇒^BKD=^MDB=1200
Vậy ^BKD=1200
Câu 33 : Cho hình thang vuông ABCD (ˆA=ˆD=900) có AB = 4cm, CD = 9cm, BC = 13cm. Gọi M là trung điểm của AD. Tính ^BMC .
Đáp án : D
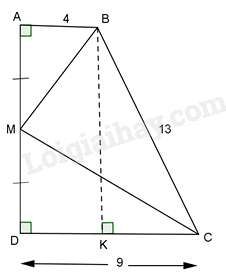
Kẻ BK⊥CD(K∈CD) thì tứ giác ABKD là hình có 3 góc vuông nên nó là hình chữ nhật.
Do đó: DK=AB=4(cm)⇒KC=DC−DK=9−4=5(cm)
Tam giác KBC vuông tại K, theo định lý Pytago ta có:
BC2=CK2+KB2 hay 132=52+KB2⇒KB=12(cm) nên ⇒AD=KB=12(cm)
M là trung điểm của AD nên AM=MD=12AD=6(cm)
Xét ΔAMB và ΔDCM có: ABDM=46=69=AMDC,^MAB=^MDC=900
⇒ΔAMB∽ΔDCM(c−g−c)
⇒^AMB=^DCM mà ^DMC+^DCM=900
⇒^AMB+^DCM=900⇒^BMC=900
Đáp án : D
ΔMNP có ˆM=90∘ , ˆP=50∘ ⇒ˆN=40∘ .
ΔMNP và ΔDEF có ˆM=ˆD (gt) cần thêm điều kiện ˆE=40∘ thì ⇒ˆN=ˆE=40∘
Lúc này ΔMNP∽ΔDEF (g – g ).
Câu 35 : Nếu ΔDEF và ΔSRK có ˆD=70∘ ; ˆE=60∘ ; ˆS=70∘ ; ˆK=50∘ thì
Đáp án : A
ΔDEF có ˆD+ˆE+ˆF=180∘⇒70∘+60∘+ˆF=180∘⇒ˆF=50∘ .
ΔDEF và ΔSRK có ˆD=ˆS=70∘ và ˆF=ˆK=50∘ nên ΔDEF∽ΔSRK (g – g).
Suy ra DESR=DFSK=EFRK .
Câu 36 : Cho hình vẽ. Khẳng định nào sao đây đúng
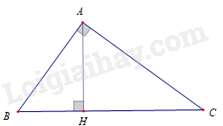
ΔABC∽ΔAHB .
Đáp án : D
ΔABC và ΔHBA có góc ˆB chung, ^BAC=^AHB=90∘ nên ΔABC∽ΔHBA (g – g)
Câu 37 : Cho ΔABC vuông tại A, đường cao AH. Hệ thức nào sau đây đúng?
Đáp án : C
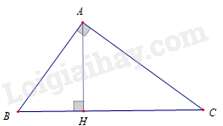
Xét ΔHCA và ΔHAB có:
^HAC=ˆB (Vì cùng phụ với ^HAB ); ^CHA=^AHB=90∘
nên ΔHCA∽ΔHAB (g – g ) ⇒AHBH=CHAH⇔AH2=BH.CH.
Câu 38 : Cho hình thang ABCD (AB//CD), O là giao điểm hai đường chéo AC và BD. Khẳng định nào sau đây đúng
Đáp án : C
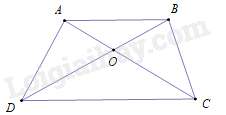
Vì AB//CD (gt) nên ^ABO=^ODC (cặp góc so le trong) .
ΔOAB và ΔOCD có:
^ABO=^ODC (chứng minh trên); ^AOB=^COD (hai góc đối đỉnh)
Nên ΔOAB∽ΔOCD (g – g ).
Câu 39 : Cho hình thang ABCD (AB//CD), O là giao điểm hai đường chéo AC và BDKhẳng định nào sau đây đúng
Đáp án : B
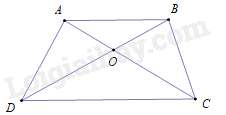
Vì AB//CD (gt) nên ^ABO=^ODC (cặp góc so le trong) .
ΔOAB và ΔODC có:
^ABO=^ODC (chứng minh trên); ^AOB=^COD (hai góc đối đỉnh)
Nên ΔOAB∽ΔOCD (g – g ) ⇒OAOC=OBOD⇔OA.OD=OB.OC.
Câu 40 : Cho hình thang ABCD(AB//CD), ^ADB=^BCD, AB=2cm, BD=√5cm. Độ dài đoạn thẳng CD là
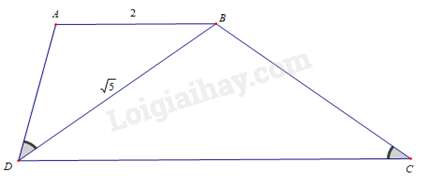
Đáp án : D
Vì AB//CD⇒^ABD=^BDC (cặp góc so le trong).
Xét ΔADB và ΔBCD có:
^ABD=^BDC (chứng minh trên); ^ADB=^BCD (gt)
Nên ΔADB∽ΔBCD (g – g ).
⇒ABBD=DBCD⇔2√5=√5CD⇔CD=√5.√52=52=2,5(cm).
Đáp án : D
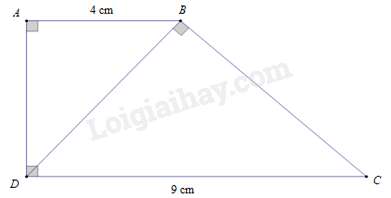
Ta có AB//CD ( vì cùng vuông góc với AD).⇒^ABD=^BDC (cặp góc so le trong)
Xét ΔABD và ΔBDC có:
^BAD=^DBC=90∘; ^ABD=^BDC (chứng minh trên)
Nên ΔABD∽ΔBDC (g – g) ⇒ABBD=BDDC⇒BD2=AB.DC=4.9=36⇒BD=6(cm).
Câu 42 : Cho ΔABC vuông tại A, đường cao AH biết BH=4cm, CH=9cm. Độ dài đoạn thẳng AH là
Đáp án : C
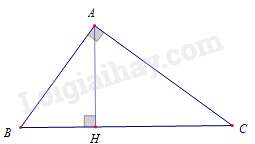
Xét ΔHCA và ΔHAB có :
^HAC=ˆB (Vì cùng phụ với ^HAB) ; ^CHA=^AHB=90∘
nên ΔHCA∽ΔHAB (g – g ) ⇒AHBH=CHAH⇔AH2=BH.CH .
⇔AH2=4.9=36⇒AH=6(cm) .
Câu 43 : Cho hình vẽ, biết ^ACB=^ABD, AB=3cm, AC=4,5cm. Độ dài đoạn thẳng AD là
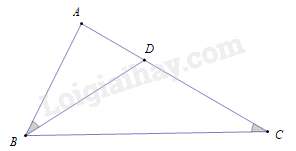
Đáp án : A
Xét ΔABC và ΔADB có:
Góc A chung, ^ACB=^ABD (gt)
Nên ΔABC∽ΔADB (g– g ) ⇒ABAD=ACAB⇔AD=AB.ABAC=3.34,5=2(cm)
Câu 44 : Cho ΔABC vuông tại A có AB=30cm, AC=40cm. Kẻ đường cao AH(H∈BC). Độ dài đường cao AH là
Đáp án : B
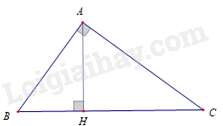
ΔABC vuông tại A nên BC=√AB2+AC2=√302+402=√2500=50(cm).
ΔABC và ΔHBA có góc B chung, ^BAC=^AHB=90∘ nên ΔABC∽ΔHBA (g – g ).
⇒ACAH=BCAB⇔40AH=5030⇔AH=40.3050=24(cm).
Câu 45 : ΔABC cân tại A, hai đường cao AH và BK, cho BC=6cm, AB=5cm. Độ dài đoạn thẳng BK là
Đáp án : B
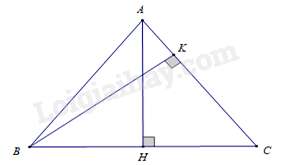
Ta có ΔABC cân tại A ⇒AC=AB=5(cm).
Vì ΔABC cân tại A nên AH là đường cao đồng thời là đường trung tuyến ứng với cạnh BC ⇒HB=HC=BC2=62=3(cm).
Áp dụng định lí Pytago vào tam giác vuông ABH ta có:
AH2=AB2−HB2=52−32=16 ⇒AH=4(cm)
Xét ΔAHC và ΔBKC có: góc C chung; ^AHC=^BKC=90∘.
Nên ΔAHC∽ΔBKC ( g – g )⇒AHBK=CACB⇔BK=AH.CBCA=4.65=4,8(cm).
Câu 46 : ΔABC vuông tại A có ˆB=60∘, BD là phân giác ˆB, AC=18cm. Độ dài đoạn thẳng BD là
Đáp án : A
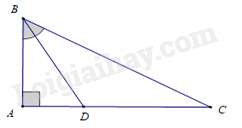
ΔABC có ˆA=90∘ nên ˆB+ˆC=90∘⇒^ACB=30∘.
Vì BD là phân giác của ˆB nên ^ABD=^DBC=12^ABC=30∘.
Xét ΔABC và ΔADB có: ^ACB=^ABD=30∘; ˆA chung
Nên ΔABC∽ΔADB ( g – g ) ⇒BCBD=ACAB⇔BD=AB.BCAC.
Xét ΔABC có ˆA=90∘, ˆC=30∘ nên ΔABC là nửa tam giác đều ⇒BC=2AB.
Áp dụng định lí Pytago vào ΔABC có:
BC2=AB2+AC2⇔(2AB)2=AB2+182⇔3AB2=324⇔AB=√108cm.
⇒BC=2√108cm. Từ đó BD=AB.BCAC=√108.2√10818=12(cm).
Câu 47 : Nếu ΔABC và ΔDEF có ˆA=ˆD , ˆC=ˆF thì
ΔABC∽ΔDEF .
ΔCAB∽ΔDEF .
ΔABC∽ΔDFE .
ΔCAB∽ΔDFE
Đáp án : A
Xét ΔABC và ΔDEF có ˆA=ˆD , ˆC=ˆF nên ΔABC∽ΔDEF (g – g)
Câu 48 : Nếu ΔABC và ΔDEF có ˆA=70∘ , ˆC=60∘ , ˆE=50∘ , ˆF=70∘ thì
Đáp án : B
ΔABC có ˆA+ˆB+ˆC=180∘⇒70∘+ˆB+60∘=180∘⇔ˆB=50∘ .
ΔABC và ΔFED có ˆA=ˆF=70∘ , ˆB=ˆE=50∘ nên ΔABC∽ΔFED (g – g ).
Câu 49 : Nếu ΔABC và ΔFED có ˆA=ˆF ,cần thêm điều kiện gì dưới đây để ΔABC∽ΔFED ?
Đáp án : B
ΔABC và ΔFED có ˆA=ˆF , ˆB=ˆE nên ΔABC∽ΔFED (g – g).
Câu 50 : Cho ΔABC∽ΔA′B′C′ (g – g ). Khẳng định nào sau đây đúng
Đáp án : B
ΔABC∽ΔA′B′C′⇒ABAC=A′B′A′C′
Câu 51 : Cho hình vẽ, khẳng định nào sau đây đúng
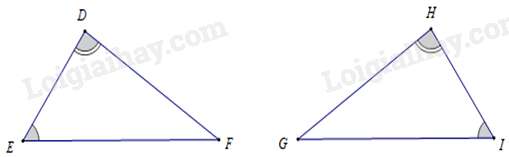
ΔHIG∽ΔDEF .
ΔIGH∽ΔDEF .
ΔHIG∽ΔDFE .
ΔHGI∽ΔDEF .
Đáp án : A
ΔHIG và ΔDEF có ˆH=ˆD , ˆI=ˆE (gt) nên ΔHIG∽ΔDEF (g – g ).
Câu 52 : Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
Đáp án : B
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Câu 53 : Nếu ΔABC và ΔMNP có ˆA=ˆN ; ˆB=ˆM thì
ΔABC∽ΔMNP .
ΔCAB∽ΔNMP .
ΔABC∽ΔPMN .
ΔABC∽ΔNMP .
Đáp án : D
ΔABC và ΔNMP có ˆA=ˆN , ˆB=ˆM nên ΔABC∽ΔNMP (g – g ).
Xem thêm các bài giải Trắc nghiệm Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: