Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 8.
Trắc nghiệm Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
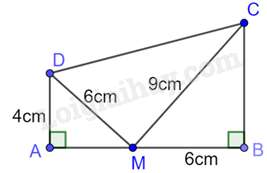
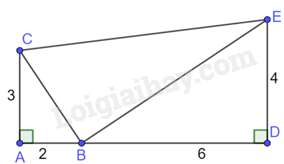
Câu 1 : Cho tứ giác ABCD có AB=9cm,AC=6cm,AD=4,^ADC=^ACB=900 (như hình vẽ)
Khẳng định nào sau đây đúng?
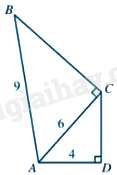
Đáp án : A
Xét tam giác ADC và tam giác ACB có: ^ADC=^ACB=900, ACAB=ADAC(=23)
Do đó, ΔADC∽ΔACB.
Do đó, ^BAC=^CAD
Câu 2 : Cho hình vẽ sau:
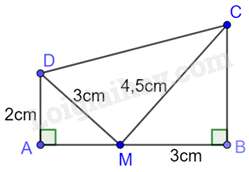
Khẳng định nào sau đây là đúng?
Đáp án : B
Tam giác ADM và tam giác BMC có:
ˆA=ˆB=900,ADMB=DMMC(=23)
Do đó, ΔAMD∽ΔBCM nên ^ADM=^BMC
Mà: ^AMD+^ADM=900, do đó, ^AMD+^BMC=900
Lại có: ^AMD+^DMC+^CMB=1800
Suy ra: ^DMC=1800−(^AMD+^BMC)=900
Câu 3 : Một ngôi nhà với hai mái lệch AB, CD được thiết kế như hình vẽ dưới đây sao cho CD=6m,AB=4m,HA=2m,AC=1m.
Khẳng định nào sau đây là đúng?
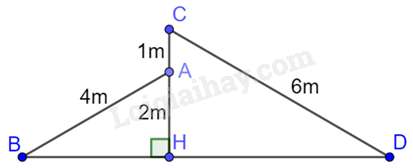
Đáp án : C
Xét tam giác ABH và tam giác CDH có:
^AHB=^CHD=900,AHCH=ABCD(=23)
Do đó, ΔABH∽ΔCDH
Suy ra: ˆB=ˆD
Mà ˆC+ˆD=900 nên ˆB+ˆC=900
Câu 4 : Cho tam giác ABC vuông tại A, AC=4cm,BC=6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho BD=9cm. Số đo góc ABD bằng bao nhiêu độ?
Đáp án : B
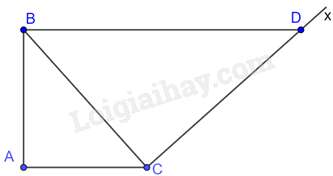
Tam giác ABC và tam giác CDB có:
ˆA=^BCD=900,ACBC=BCBD(=23)
Do đó, ΔABC∽ΔCDB nên ^ABC=^BDC
Mà ^BDC+^CBD=900 nên ^ABC+^CBD=900 hay ^ABD=900
Câu 5: Cho hình vẽ:
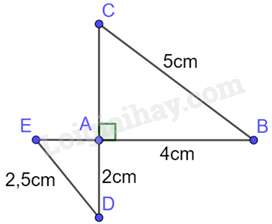
Chọn đáp án đúng.
Đáp án : B
Tam giác ADE và tam giác ACB có:
^DAE=^CAB=900,ADAB=EDCB(=12)
Do đó, ΔADE∽ΔABC
Suy ra: ˆC=ˆE
Câu 6 : Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: ABDE=BCFE
Chọn đáp án đúng
Đáp án : D
Tam giác ABC và tam giác DEF có: ^BAC=^EDF=900,ABDE=BCFE nên ΔABC∽ΔDEF.
Câu 7 : Hai tam giác vuông đồng dạng với nhau khi:
Đáp án : C
Câu 8 : Cho hai hình sau:
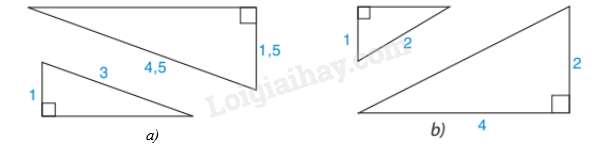
Chọn đáp án đúng.
Đáp án : A
Hình b không thể hiện hai tam giác đồng dạng
Câu 9 : Cho tam giác ABC vuông tại A có: AB=3cm,BC=5cm và tam giác MNP vuông tại M có MN=6cm,NP=10cm. Khi đó,
Đáp án : B
Do đó, ΔABC∽ΔMNP
Câu 10 : Cho hai tam giác vuông ABC và ADE có các kích thước như hình dưới. Khẳng định nào sau đây đúng?
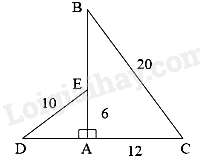
Đáp án : B
Ta có: AEAC=612=12;DEBC=1020=12 nên AEAC=DEBC
Tam giác ADE và tam giác ABC có: ^DAE=^BAC=900,AEAC=DEBC nên ΔADE∽ΔABC
Câu 11 : Tam giác ABH vuông tại H có AB=20cm,BH=12cm. Trên tia đối của tia HB lấy điểm C sao cho AC=53AH. Khi đó, số đo góc BAC bằng:
Đáp án : B
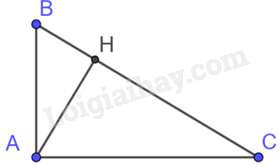
Ta có: ABBH=2012=53;AC=53AH⇒ACAH=53⇒ABBH=ACAH⇒ABAC=BHAH
Tam giác ABH và tam giác CAH có: ^AHB=^AHC=900,ABAC=BHAH
Do đó, ΔABH∽ΔCAH
Suy ra: ^CAH=^ABH
Mà ^BAH+^ABH=900 nên ^BAH+^CAH=900 hay ^BAC=900
Câu 12 : Tam giác ABH vuông tại H có AB=10cm,BH=6cm. Trên tia đối của tia HB lấy điểm C sao cho 3AC=5AH. Khẳng định nào sau đây là đúng?
Đáp án : C
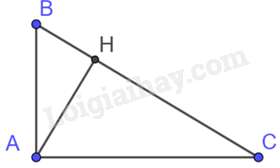
Ta có: ABBH=106=53;3AC=5AH⇒ACAH=53⇒ABBH=ACAH⇒ABAC=BHAH
Tam giác ABH và tam giác CAH có: ^AHB=^AHC=900,ABAC=BHAH
Do đó, ΔABH∽ΔCAH
Suy ra: ^CAH=^ABH
Mà ^BAH+^ABH=900 nên ^BAH+^CAH=900 hay ^BAC=900
Do đó, tam giác ABC vuông tại A.
Theo định lý Pythagore ta có:
BC2=AB2+AC2
Câu 13 : Cho tam giác ABC cân tại A, đường cao AH và M là trọng tâm của tam giác ABC; tam giác A’B’C’ cân tại A’, đường cao A’H và M’ là trọng tâm tâm của tam giác A’B’C’. Biết rằng BHB′H′=ABA′B′=3. Chọn đáp án đúng.
Đáp án : D
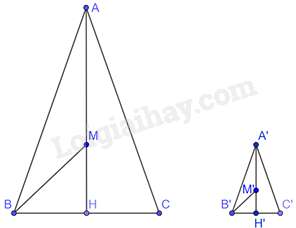
Tam giác ABC cân tại A, AH là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, M thuộc AH. Do đó, 3MH=AH
Tam giác A’B’C’ cân tại A’, A’H’ là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, M’ thuộc A’H’. Do đó, 3M′H′=A′H′
Xét tam giác ABH và tam giác A’B’H’ có: ^AHB=^A′H′B′=900,BHB′H′=ABA′B′=3
Suy ra: ΔAHB∽ΔA′H′B′, do đó, AHA′H′=3⇒3HM3H′M′=3⇒HMH′M′=3
Tam giác BHM và tam giác B’H’M’ có:
^MHB=^M′H′B′=900,HMHM′=BHB′H′=3
Do đó, ΔBMH∽ΔB′M′H′ nên BMB′M′=BHB′H′=3
Câu 14 : Cho tam giác ABC vuông tại A, AC=4cm,BC=6cm.Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho BD=9cm. Diện tích tam giác ABD bằng:
Đáp án : B
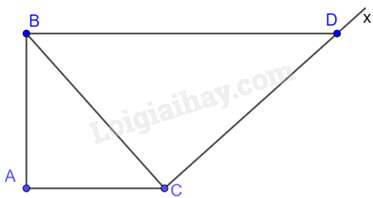
Tam giác ABC và tam giác CDB có:
ˆA=^BCD=900,ACBC=BCBD(=23)
Do đó, ΔABC∽ΔCDB nên ^ABC=^BDC
Mà ^BDC+^CBD=900 nên ^ABC+^CBD=900 hay ^ABD=900
Do đó, tam giác ABD vuông tại B
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có:
AB2+AC2=BC2
AB2=BC2−AC2=20
AB=√20cm
Do tam giác ABD vuông tại B nên diện tích tam giác ABD là:
12AB.BD=12.√20.9=92√20(cm2)
Câu 15 : Tam giác ABH vuông tại H có AB=25cm,BH=15cm. Trên tia đối của tia HB lấy điểm C sao cho AC=53AH. Chu vi tam giác AHC là:
Đáp án : A
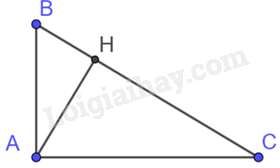
Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có: AB2=BH2+AH2
AH2=AB2−BH2=400 nên AH=20cm⇒AC=53.20=1003(cm)
Ta có: ABBH=2515=53;AC=53AH⇒ACAH=53⇒ABBH=ACAH⇒ABAC=BHAH
Tam giác ABH và tam giác CAH có: ^AHB=^AHC=900,ABAC=BHAH
Do đó, ΔABH∽ΔCAH⇒ABAC=AHCH⇒CH=AH.ACAB=803cm
Vậy chu vi tam giác AHC là: AH+HC+AC=20+803+1003=80(cm)
Câu 16 : Cho hình vẽ:
Chu vi tam giác DMC là:
Đáp án : B
Tam giác ADM và tam giác BMC có:
ˆA=ˆB=900,ADMB=DMMC(=23)
Do đó, ΔAMD∽ΔBCM nên ^ADM=^BMC
Mà: ^AMD+^ADM=900, do đó, ^AMD+^BMC=900
Lại có: ^AMD+^DMC+^CMB=1800
Suy ra: ^DMC=1800−(^AMD+^BMC)=900
Do đó, tam giác DMC vuông tại M
Áp dụng định lý Pythagore vào tam giác DMC vuông tại M có:
DC2=DM2+MC2=117 nên DC=√117cm
Vậy chu vi tam giác DMC là: DM+MC+DC=6+9+√117=15+√117(cm)
Câu 17 : Cho tam giác ABC cân tại A có chu vi bằng 60cm và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng BHB′H′=BCB′C′=32. Chu vi tam giác A’B’C’ là:
Đáp án : D
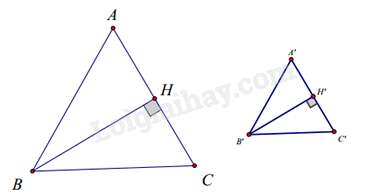
Tam giác BHC và tam giác B’H’C’ có: ^BHC=^B′H′C′=900,BHB′H′=BCB′C′=32
Do đó, ΔBHC∽ΔB′H′C′
Suy ra: ˆC=^C′, mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên ˆB=^B′=ˆC=^C′
Do đó, ΔABC∽ΔA′B′C′ nên ABA′B′=ACA′C′=BCB′C′=23
Theo tính chất dãy tỉ số bằng nhau ta có: ABA′B′=ACA′C′=BCB′C′=AB+BC+ACA′B′+B′C′+A′C′=23
Mà chu vi tam giác ABC bằng 60cm nên chu vi tam giác A’B’C’ là: 60:32=40(cm)
Câu 18 : Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng CHC′H′=BCB′C′. Biết rằng ^BAC=4^A′C′B′. Chọn đáp án đúng.
Đáp án : C
Tam giác BHC và tam giác B’H’C’ có: ^BHC=^B′H′C′=900,CHC′H′=BCB′C′
Do đó, ΔBHC∽ΔB′H′C′
Suy ra: ˆC=^C′, mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên ˆB=^B′=ˆC=^C′
Do đó, ^BAC=4^ACB=4^ABC
Lại có: ^BAC+^ACB+^ABC=1800⇒6^ACB=1800⇒^ACB=300⇒^BAC=1200
Câu 19 : Cho điểm B nằm trên đoạn thẳng AC sao cho AB=6cm,BC=24cm. Vẽ về một phía của AC tia Ax và Cy vuông góc với AC. Trên tia Ax lấy điểm E sao cho EB=10cm, trên tia Cy lấy điểm D sao cho BD=30cm.
Cho các khẳng định sau:
1. Tam giác EBD là tam giác nhọn.
2. Diện tích tam giác EBD bằng 150cm2.
3. Chu vi tam giác EBD bằng 60cm.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
Đáp án : B
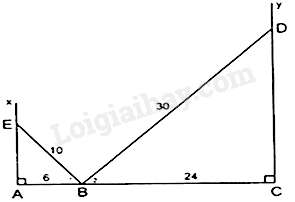
Áp dụng định lý Pythagore vào tam giác CDB vuông ở C ta có:
BD2=DC2+CB2
DC2=302−242=324⇒DC=18cm
Xét tam giác BEA và tam giác DBC có:
ˆA=ˆC=900,BEBD=BADC(=13)
Do đó, ΔBEA∽ΔDBC, suy ra ^EBA=^BDC
Mà ^DBC+^BDC=900⇒^DBC+^EBA=900
Lại có: ^DBC+^EBD+^EBA=1800 nên ^EBD=900
Do đó, tam giác BDE vuông tại B.
Diện tích tam giác EBD là: 12BE.BD=12.10.30=150(cm2)
Áp dụng định lý Pythagore vào tam giác EBD vuông tại B có:
ED2=EB2+BD2=102+302=1000⇒ED=√1000cm
Chu vi tam giác EBD là: EB+BD+ED=10+30+√1000=40+√1000(cm)
Vậy có 1 khẳng định đúng.
Câu 20 : Cho hai hình chữ nhật ABCD và A’B’C’D’ thỏa mãn AC=3AB,B′D′=3A′B′
Nếu AB=2A′B′ và diện tích hình chữ nhật ABCD là 12m2 thì diện tích hình chữ nhật A’B’C’D’ là bao nhiêu?
Đáp án : D
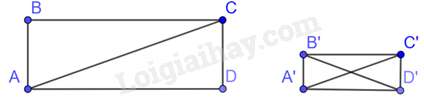
Vì AC=3AB⇒ABAC=13,B′D′=3A′B′⇒A′B′B′D′=13
Do đó, ABAC=A′B′B′D′⇒ABA′B′=ACB′D′
Tam giác ABC và tam giác A’B’D’ có:
^ABC=^B′A′D′=900;ABA′B′=ACB′D′ nên ΔABC∽B′A′D′(1)
Chứng minh được ΔB′A′D′=ΔA′B′C′(2)
Từ (1) và (2) ta có: ΔABC∽ΔA′B′C′
Do đó, ABA′B′=ACA′C′=BCB′C′=12
Diện tích hình chữ nhật ABCD là: SABCD=AB.BC
Diện tích hình chữ nhật A’B’C’D’ là: SA′B′C′D′=A′B′.B′C′
Do đó: SABCDSA′B′C′D′=AB.BCA′B′.B′C′=ABA′B′.BCB′C′=2.2=4
⇒SA′B′C′D′=124=3(cm2)
Câu 21 : Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: ABDE=ACDF
Chọn đáp án đúng
Đáp án : D
Tam giác ABC và tam giác DEF có: ^BAC=^EDF=900,ABDE=ACDF nên ΔABC∽ΔDEF
Câu 22 : Hai tam giác vuông đồng dạng với nhau khi:
Đáp án : C
Hai cạnh góc vuông của tam giác này lần lượt bằng hai cạnh góc vuông của tam giác kia thì khi đó tỉ lệ của hai cạnh tam giác vuông bằng 1. Do đó, hai tam giác cũng đồng dạng với nhau.
Câu 23 : Cho hình vẽ sau:
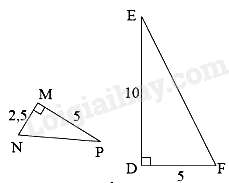
Chọn đáp án đúng.
Đáp án : A
Tam giác MNP và tam giác DFE có: ˆM=ˆD=900,MNDF=MPDE(=12) nên ΔMNP∽ΔDFE
Câu 24 : Cho tam giác ABC vuông tại A có: AB=3cm,AC=5cm và tam giác MNP vuông tại M có MN=12cm,MP=20cm. Khi đó,
Đáp án : B
Do đó, ΔABC∽ΔMNP
Câu 25 : Cho hình vẽ:
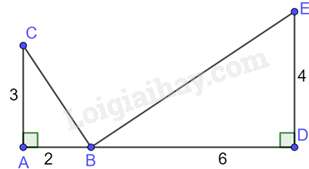
Đáp án : B
Ta có: ABDE=24=12;ACBD=36=12 nên ABDE=ACBD
Tam giác ABC và tam giác DEB có: ^BAC=^BDE=900,ABDE=ACBD nên ΔABC∽ΔDEB
Câu 26 : Cho hình vẽ:
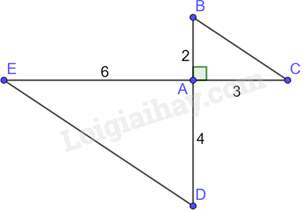
Đáp án : A
Xét tam giác ABC và tam giác ADE có: ^BAC=^DAE=900, ABAD=ACAE(=12)
Do đó, ΔABC∽ΔADE
Do đó, ˆB=ˆD
Câu 27 : Cho hình vẽ:
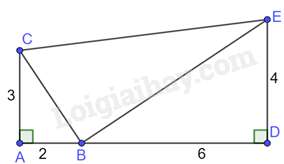
Chọn đáp án đúng
Đáp án : D
Ta có: ABDE=24=12;ACBD=36=12 nên ABDE=ACBD
Tam giác ABC và tam giác DEB có: ^BAC=^BDE=900,ABDE=ACBD nên
Do đó, ^CBA=^BED
Mà ^BED+^EBD=900 nên ^ABC+^EBD=900
Câu 28 : Cho hình vẽ dưới đây:
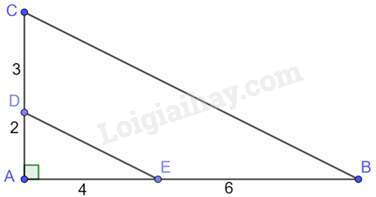
Chọn đáp án đúng
Đáp án : C
Ta có: AC=5;AB=10
Xét tam giác ADE và tam giác ACB có:
ˆAchung,ADAC=AEAB(=25)
Do đó, ΔADE∽ΔACB
Suy ra: ˆC=^ADE
Câu 29 : Cho hình vẽ:
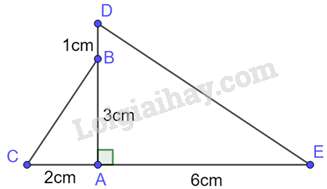
Khẳng định nào sau đây là đúng?
Đáp án : C
Tam giác ABC và tam giác AED có: ^CAB=^DAE=900,ACAD=ABAE(=12)
Do đó, ΔABC∽ΔAED nên ˆD=ˆC
Mà ˆC+^ABC=900 nên ˆD+^ABC=900
Câu 30 : Cho hình vẽ:
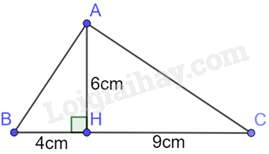
Chọn đáp án đúng.
Đáp án : A
Tam giác AHB và tam giác CAH có:^AHB=^AHC=900,BHAH=AHHC(=23)
Do đó, ΔAHB∽ΔCAH
Suy ra: ^BAH=ˆC
Câu 31 : Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có ABA′B′=ACA′C′=12. Gọi M, M’ lần lượt là trung điểm của BC và B’C’. Khi đó, tỉ số AMA′M′ bằng
Đáp án : C
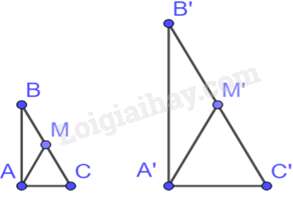
Tam giác ABC và tam giác A’B’C có: ^BAC=^B′A′C′=900,ABA′B′=ACA′C′
Do đó, ΔABC∽ΔA′B′C′
Suy ra: ABA′B′=ACA′C′=BCB′C′=12
Mà M là trung điểm của BC nên BC=2AM, M’ là trung điểm của B’C’ nên B′C′=2A′M′
Do đó, AMA′M′=12
Câu 32 : Trên đoạn BC=13cm, đặt đoạn BH=4cm. Trên đường vuông góc với BC tại H, lấy điểm A sao cho HA=6cm
Cho các khẳng định sau:
1. Số đo góc BAC bằng 80 độ
2. AB.AC=AH.BC
3. ˆB>^CAH
Có bao nhiêu khẳng định đúng?
Đáp án : B
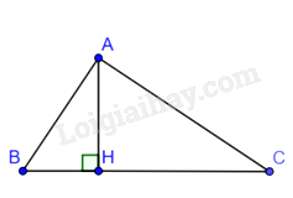
Ta có: HC=BC−BH=9(cm)
Tam giác AHB và tam giác CAH có:
^AHB=^AHC=900,BHAH=AHHC(=23)
Do đó, ΔAHB∽ΔCAH
Suy ra: ˆB=^CAH(khẳng định (3) sai)
Mà ˆB+^BAH=900 nên ^BAH+^CAH=900 hay ^BAC=900 (khẳng định (1) sai)
Do đó, tam giác ABC vuông tại A.
Diện tích tam giác ABC là: 12AB.AC=12AH.BC⇒AB.AC=AH.BC(khẳng định (2) đúng)
Vậy có 1 khẳng định đúng
Câu 33 : Cho hình thang ABCD vuông tại A và D. Biết CD=2AB=2AD=2a và BC=a√2. Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Khi đó:
Đáp án : A
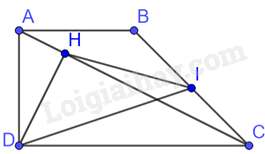
Áp dụng định lý Pythagore vào tam giác ADB vuông tại A có: BD2=AD2+AB2=a2+a2=2a2⇒BD=a√2
Tam giác ABD vuông cân tại A nên ^ADB=450
Ta có: BD2+BC2=2a2+2a2=4a2=CD2 nên tam giác BDC vuông tại B, do đó, ^DBC=900
Xét tam giác ADC và tam giác IBD có:
^ADC=^IBD=900,ADIB=DCBD
Do đó, ΔADC∽ΔIBD
Suy ra, ^ACD=^BDI
Mà ^ADH=^ACD (cùng phụ với góc HDC)
Do đó, ^ADH=^BDI
Mà ^ADH+^BDH=450⇒^BDI+^BDH=450 hay ^HDI=450
Câu 34 : Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D. Kẻ OM vuông góc với CD tại M. Khi đó:
Đáp án : D
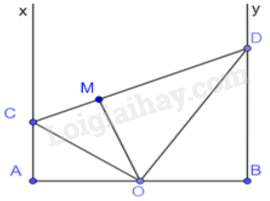
Tam giác OAC và tam giác DBO có: ^OAC=^DBO=900,^COA=^BDO (cùng phụ với góc DOB)
Do đó, ΔOAC∽ΔDBO⇒OCOD=ACOB
Mà OA=OB⇒OCOD=ACOA⇒OCAC=ODOA
Tam giác OCD và tam giác ACO có: ^CAO=^COD=900,OCAC=ODOA
Do đó, ΔOCD∽ΔACO⇒^OCD=^ACO
Chứng minh được ΔOAC=ΔOMC(ch−gn)⇒AC=MC
Câu 35 : Cho tam giác ABC vuông tại A có M là trung điểm của BC. Gọi I là hình chiếu của M trên AC. Chọn đáp án đúng.
Đáp án : C
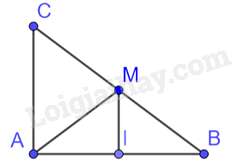
Tam giác ABC vuông tại A có AM là trung tuyến nên AM=MB=12BC
Do đó, tam giác AMB cân tại M. Do đó, MI là đường cao đồng thời là đường trung tuyến nên AI=12AB⇒AIAB=12
Tam giác ABC có: M là trung điểm của CB, I là trung điểm của AB nên MI là đường trung bình của tam giác ABC nên MIAC=12
Tam giác ABC và tam giác AIM có:
^BAC=^MIA=900,AIAB=MIAC(=12) nên ΔIAM∽ΔABC
Do đó, SABCSAMI=(MIAC)2=14
Câu 36 : Cho hình vẽ:
Chọn đáp án đúng
Đáp án : B
Ta có: ABDE=24=12;ACBD=36=12 nên ABDE=ACBD
Tam giác ABC và tam giác DEB có: ^BAC=^BDE=900,ABDE=ACBD nên ΔABC∽ΔDEB
Do đó, ^CBA=^BED
Mà ^BED+^EBD=900 nên ^ABC+^EBD=900
Mà ^ABC+^EBD+^CBE=1800 nên ^CBE=900
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có: BC2=AB2+AC2=13
Áp dụng định lý Pythagore vào tam giác BDE vuông tại D có: BE2=DE2+BD2=52
Áp dụng định lý Pythagore vào tam giác BCE vuông tại B có: CE2=BE2+BC2=65 nên CE=√65
Câu 37 : Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’ có chu vi bằng 30cm, các đường cao BH và B’H’. Biết rằng BHB′H′=HCH′C′=32. Chu vi tam giác ABC là:
Đáp án : D
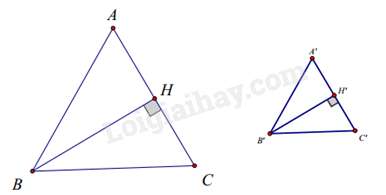
Tam giác BHC và tam giác B’H’C’ có: ^BHC=^B′H′C′=900,BHB′H′=HCH′C′=32
Do đó, ΔBHC∽ΔB′H′C′
Suy ra: + BHB′H′=HCH′C′=BCB′C′=32
+ ˆC=^C′, mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên ˆB=^B′=ˆC=^C′
Do đó, ΔABC∽ΔA′B′C′ nên ABA′B′=ACA′C′=BCB′C′=32
Theo tính chất dãy tỉ số bằng nhau ta có: ABA′B′=ACA′C′=BCB′C′=AB+BC+ACA′B′+B′C′+A′C′=32
Mà chu vi tam giác A’B’C’ bằng 30cm nên chu vi tam giác ABC là: 30.32=45(cm)
Câu 38 : Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng BHB′H′=HCH′C′. Biết rằng ^A′B′C′=17^BAC. Chọn đáp án đúng
Đáp án : A
Tam giác BHC và tam giác B’H’C’ có: ^BHC=^B′H′C′=900,BHB′H′=HCH′C′
Do đó, ΔBHC∽ΔB′H′C′
Suy ra: ˆC=^C′, mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên ˆB=^B′=ˆC=^C′
Do đó, ^BAC=7^ACB=7^ABC
Lại có: ^BAC+^ACB+^ABC=1800⇒9^ACB=1800⇒^ACB=200⇒^BAC=1400
Câu 39 : Cho hình thang vuông ABCD, (ˆA=ˆD=900) có AB=4cm,CD=9cm và BC=13cm. Khoảng cách từ M đến BC bằng:
Đáp án : C
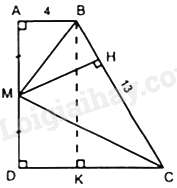
Kẻ BK vuông góc với CD tại K.
Tứ giác ABKD có: ˆA=ˆD=^BKD=900 nên tứ giác ABKD là hình chữ nhật, do đó, KC=DC−DK=5cm
Áp dụng định lý Pythagore vào tam giác BKC vuông tại K ta có:
BC2=CK2+KB2⇒KB2=144⇒KB=12cm
Vì tứ giác ABKD là hình chữ nhật nên AD=BK=12cm do đó AM=MD=6cm
Xét tam giác ABM và tam giác DMC có:
^BAM=^MDC=900,ABDM=AMDC(=23)
Do đó, ΔABM∽ΔDMC
Suy ra, ^AMB=^DCM
Mà ^DMC+^MCD=900⇒^DMC+^AMB=900
Ta có: ^DMC+^BMC+^AMB=1800⇒^BMC=900
Do đó, tam giác BMC vuông tại M.
Kẻ MH vuông góc với BC tại H thì MH là khoảng cách từ M đến BC.
Áp dụng định lý Pythagore vào hai tam giác ABM và tam giác DMC ta được:
{BM2=MA2+AB2=62+42=52MC2=CD2+DM2=92+62=117
Do đó, BM=2√13cm,MC=3√13cm
Diện tích tam giác BMC vuông tại M có:
12BM.MC=12MH.BC⇒2√13.3√13=13.MH⇒MH=6cm
Câu 40 : Cho tam giác ABC vuông tại A, AC=3AB=3a. Lấy các điểm D, E thuộc AC sao cho AD=DE=EC. Khi đó,
Đáp án : B
Lời giải :
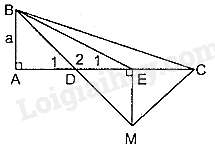
Ta có: AD=DE=EC=a
Vẽ M đối xứng với B qua D.
Tam giác BAD vuông tại A có AB=AD nên tam giác ABD vuông cân tại A. Suy ra: ^ABD=^ADB=450
Chứng minh được ΔABD=ΔEMD nên ^ABD=^EMD=450,^MED=^BAD=900 và BD=DM=12BM,ME=AB=a
Tam giác MEC có ME là đường cao đồng thời là đường trung tuyến nên tam giác DME cân tại M. Do đó, ME là đường phân giác. Do đó, ^DMC=2^DME=900
Áp dụng định lý Pythagore vào tam giác ABD vuông tại A có: BD=a√2⇒BM=2a√2
Áp dụng định lý Pythagore vào tam giác MEC vuông tại E có: MC=a√2
Ta có: ABMC=aa√2=1√2;AEBM=2a2a√2=1√2⇒ABMC=AEBM
Tam giác EAB và tam giác BMC có:
^BAE=^BMC=900,ABMC=AEBM nên ΔEAB∽ΔBMC
Do đó, ^BEA=^MBC
Mà ^BEA+^BCA=^MBC+^BCA=^BDA=450
Câu 41 : Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: ˆB=ˆF
Chọn đáp án đúng
Đáp án : B
Tam giác ABC và tam giác DEF có: ^BAC=^EDF=900,ˆB=ˆF nên ΔABC∽ΔDFE(g.g)
Câu 42 : Cho hình vẽ:
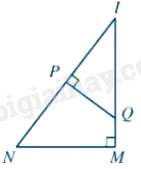
Chọn đáp án đúng
Đáp án : A
Lời giải:
Do đó, ΔIPQ∽ΔIMN(g.g)
Câu 43 : Cho tam giác ABC vuông tại A và DEF vuông tại D. Để ΔABC∽ΔDEF thì ta cần thêm điều kiện:
Đáp án : A
Điều kiện cần thêm là: ˆB=ˆE
Câu 44 : Cho các mệnh đề sau. Chọn câu đúng.
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Đáp án : A
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Vậy (I) đúng, (II) sai.
Câu 45 : Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
Đáp án : A
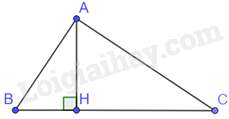
Tam giác ACH và tam giác CBA có: ^AHC=^BAC=900,ˆCchung
Do đó, ΔACH∽ΔBCA(g.g)
Câu 46 : Cho hình vẽ:

Chọn đáp án đúng.
Đáp án : B
Ta có: ˆA+ˆC=ˆA+ˆE(=900)⇒ˆC=ˆE
Xét tam giác ABE và tam giác DCB có: ^ABE=^DBC=900,ˆE=ˆC
Do đó, ΔABE∽ΔDBC(g.g)
Do đó, BCBE=BDBA
Câu 47 : Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM=2m,AM⊥AB và đo được góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A’M’B’ vuông tại A’ có A′M′=1cm,^A′M′B′=^AMB và đo được A′B′=5cm (hình vẽ dưới). Khoảng cách từ A đến B bằng:

Đáp án : D
Đổi 1cm=0,01m;5cm=0,05m
Tam giác AMB và tam giác A’M’B’ có: ^BAM=^B′A′M′=900,^AMB=^A′M′B′
Do đó,ΔAMB∽ΔA′M′B′(g.g)
Suy ra, ABA′B′=AMA′M′=20,01=200⇒AB=200.A′B′=10(m)
Câu 48 : Một ngọn tháp cho như hình vẽ dưới đây, biết rằng MB=20m,MF=2m,FE=1,65m.
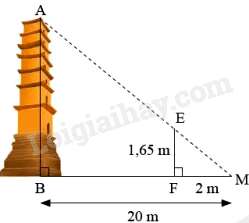
Chiều cao AB của ngọn tháp bằng:
Đáp án : C
Xét tam giác AMB và tam giác EMF có:
^ABM=^EFM=900,ˆMchung
Do đó, ΔABM∽ΔEFM(g.g)
Suy ra: ABFE=BMFM=202=10⇒AB=10.FE=10.1,65=16,5(m)
Câu 49 : Cho hình vẽ:
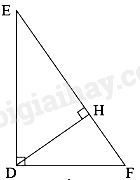
Khẳng định nào sau đây là đúng?
Đáp án : B
Ta có: ^EDH+^HDF=ˆF+^HDF(=900)⇒^EDH=ˆF
Tam giác EDH và tam giác DFH có:
^EHD=^FHD=900,^EDH=ˆF
Do đó, ΔEDH∽ΔDFH(g.g) nên DHFH=EHDH⇒DH2=EH.FH
Câu 50 : Cho tam giác ABC vuông tại A có ˆB=300, tam giác MNP vuông tại M có ˆN=600.
Chọn đáp án đúng.
Đáp án : A
Tam giác ABC vuông tại A nên ˆB+ˆC=900⇒ˆC=900−ˆB=600
Tam giác ABC và tam giác MNP có: ˆA=ˆM=900,ˆC=ˆN(=600)
Do đó, ΔABC∽ΔMPN(g.g)⇒ABMP=BCPN⇒AB.PN=MP.BC
Câu 51 : Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
Đáp án : C
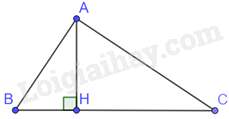
Tam giác ACH và tam giác CBA có: ^AHC=^BAC=900,ˆCchung
Do đó, ΔACH∽ΔBCA(g.g)⇒ACBC=CHAC⇒AC2=CH.BC
Câu 52 : Cho tam giác ABC cân tại A , đường cao CE . Tính AB , biết BC=24 cm và BE=9 cm.
Đáp án : B
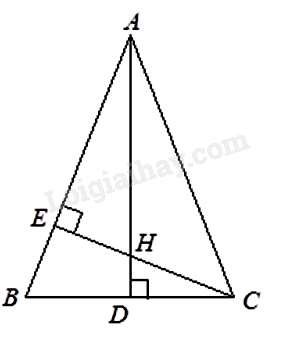
Kẻ đường cao AD . Xét ΔCBE và ΔABD có ^BEC=^ADB=90∘ và ˆB chung nên ΔCBE∽ΔABD⇒BCAB=BEBD hay 24AB=912
⇒AB=32cm .
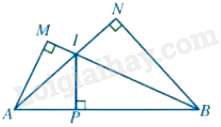
Câu 53 : Cho hình vẽ:
Chọn đáp án đúng
Đáp án : B
Tam giác ABN và tam giác AIP có: ˆN=^IPA=900,^BANchung
Do đó, ΔABN∽ΔAIP⇒ABAI=ANAP⇒AI.AN=AP.AB
Tam giác AMB và tam giác IPB có: ˆM=^IPB=900,^ABMchung
Do đó, ΔAMB∽ΔIPB⇒ABBI=BMBP⇒AB.BP=BI.BM
Vậy AI.AN+BI.BM=AP.AB+AB.PB=AB(AP+PB)=AB2
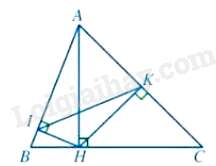
Câu 54 : Cho hình vẽ:
Chọn đáp án đúng
Đáp án : D
Tam giác AHI và tam giác ABH có: ^HAIchung,^AIH=^AHB=900
Do đó, ΔAHI∽ΔABH⇒AHAB=AIAH⇒AH2=AB.AI (1)
Tam giác AHK và tam giác ACH có: ^HACchung, ^AKH=^AHC=900
Do đó, ΔAHK∽ΔACH⇒AHAC=AKAH⇒AH2=AK.AC (2)
Từ (1) và (2) ta có: AC.AK=AB.AI
Câu 55 : Cho hình vẽ:
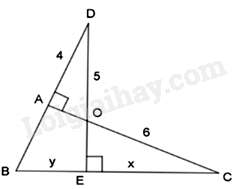
Chọn đáp án đúng.
Đáp án : B
Tam giác ADO và tam giác ECO có: ^DAO=^CEO=900,^AOD=^COE (hai góc đối đỉnh)
Do đó, ΔADO∽ΔECO⇒ADEC=DOCO⇒4x=56⇒x=4,8
Áp dụng định lý Pytago vào tam giác ADO vuông tại A ta có:
AD2+AO2=OD2 ⇒AO2=DO2−AD2=9⇒AO=3
Tam giác CEO và tam giác CAB có: ^CEO=^CAB=900,ˆCchung
Do đó, ΔCEO∽ΔCAB⇒COCB=CECA⇒COEC+EB=CECO+AO⇒64,8+y=4,86+3⇒y=6,45
Câu 56 : Cho tam giác ABC cân tại A, AC=20cm,BC=24cm. Các đường cao AD và CE cắt nhau tại H. Khi đó,
Đáp án : C

Tam giác ABC cân tại A nên BD=DC=BC2=12(cm)
Áp dụng định lý Pytago vào tam giác ADC vuông tại D ta có: AD2=AC2−DC2=162⇒AD=16cm
Tam giác CDH và tam giác ADB có: ^CDH=^ADB=900,^C1=^A1 (cùng phụ với góc B)
Do đó, ΔCDH∽ΔADB⇒HDBD=CDAD⇒HD12=1216=34
Suy ra: HD=9cm
Câu 57 : Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng HB=7cm,HC=18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
Đáp án : A

Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Tam giác AHC và tam giác ABC có: ^AHC=^BAC=900,ˆCchung. Do đó, ΔACH∽ΔBCA
Ta có: SDEC=12SABC(1) , SAHCSABC=12HC.AH12BC.AH=HCBC=1825⇒SAHC=1825SABC(2)
Từ (1) và (2) ta có: SDEC:SAHC=12:1825=2536=(56)2(3)
Tam giác DEC và tam giác AHC có: ^DEC=^AHC=900,ˆCchung
ΔDEC∽ΔAHC⇒SDECSAHC=(ECHC)2(4)
Từ (3) và (4) ta có: ECHC=56 ⇒ EC18=56⇒EC=15cm
Câu 58 : Cho hình bình hành ABCD (AC>AB) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD và H là hình chiếu của B trên AC.
Chọn đáp án đúng.
Đáp án : D
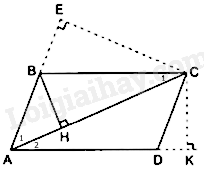
Tam giác AHB và tam giác AEC có: ^A1chung,^AHB=ˆE=900
Do đó, ΔAHB∽ΔAEC⇒AHAE=ABAC⇒AB.AE=AC.AH
Vì BC// AD (do ABCD là hình bình hành) nên ^C1=^A2 , mà ^BHC=ˆK=900
Do đó, ΔAKC∽ΔCHB⇒AKCH=ACCB⇒AK.CB=AC.CH
Vì ABCD là hình bình hành nên BC=AD
Do đó, AD.AK=AC.CH(3)
Từ (1), (2) và (3) ta có:
AB.AE+AD.AK=AC(AH+CH)=AC2
Câu 59 : Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
Đáp án : C
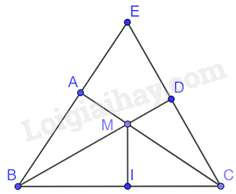
Kẻ MI vuông góc với BC tại I
Tam giác BIM và tam giác BDC có: ^BIM=^BDC=900,^MBCchung
Do đó, ΔBIM∽ΔBDC⇒BMBC=BIBD⇒BM.BD=BC.BI(1)
Chứng minh tương tự ta có: ΔICM∽ΔACB⇒CMBC=CICA⇒CM.CA=BC.CI(2)
Từ (1) và (2) ta có: BM.BD+CM.CA=BC.BI+BC.CI=BC(BI+CI)=BC2
Câu 60 : Cho tam giác ABC cân tại A, đường cao CE. Biết rằng BE=3cm,BC=8cm.
Độ dài đoạn thẳng AB là:
Đáp án : C
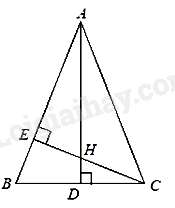
Kẻ đường cao AD của tam giác ABC.
Vì tam giác ABC cân tại A nên AD là đường cao đồng thời là đường trung tuyến
Suy ra: BD=12BC=4cm
Xét tam giác CBE và tam giác ABD có: ^BEC=^ADB=900 và góc B chung
Do đó, ΔCBE∽ΔABD(g.g)⇒BCAB=BEBD⇒AB=BD.BCBE=323(cm)
Xem thêm các bài giải Trắc nghiệm Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: