Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 8 Bài 1: Hai tam giác đồng dạng sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 8.
Trắc nghiệm Toán 8 Bài 1: Hai tam giác đồng dạng
Câu 1 : Cho ΔABC,ΔMNP biết AB=3cm;AC=4cm;BC=5cm;MN=6cm;MP=8cm;NP=10cm và ˆA=90o;ˆB=60o;ˆM=90o;ˆP=30o thì:
Đáp án : C
ΔABC có ˆC=180o−(ˆA+ˆB)=180o−(90o+80o)=30o (Định lý tổng ba góc trong tam giác )
ΔMNP có ˆN=180o−(ˆM+ˆP)=180o−(90o+30o)=60o (Định lý tổng ba góc trong tam giác)
Xét ΔABC và ΔMNP có:
ABMN=186=3;ACMP=248=3;BCNP=3010=3
⇒ABMN=ACMP=BCNP
Vậy ˆA=ˆM(=90o);ˆB=ˆN(=60o);ˆC=ˆP(=30o)
Câu 2 : Cho ΔABC∽ΔDEF biết ˆA=50o;ˆB=60o . Khi đó số đo góc D bằng
Đáp án : A
Vì ΔABC∽ΔDEF⇒ˆA=ˆD (hai góc tương ứng)
Mà ˆA=50o(gt)⇒ˆD=50o
Câu 3 : Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
Đáp án : A
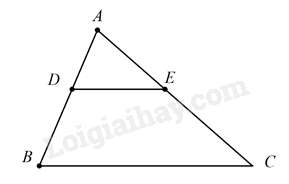
Vì DE//BC⇒ΔABC∽ΔADE(gt)
Câu 4 : Cho ΔABC∽ΔMNP theo tỉ số k1 , ΔMNP∽ΔDEF theo tỉ số k2 . Hỏi ΔABC∽ΔMNP theo tỉ số nào ?
Đáp án : C
Vì ΔABC∽ΔDEF theo tỉ số k1⇒ABDE=k1
Vì ΔMNP∽ΔDEF theo tỉ số k2⇒MNDE=k2
⇒ABMN=ABDE:MNDE=k1k2
Câu 5 : Cho ΔABC∽ΔMNP . Biết AB=5cm;BC=6cm;MN=10cm;MP=5cm . Hãy chọn đáp án đúng:
Đáp án : A
Vì ΔABC∽ΔMNP⇒ABMN=ACMP=BCNP (hai cạnh tương ứng)
⇒510=AC5=6NP⇒AC=5.510=2,5cm;NP=10.65=12cm
Câu 6 : Hãy chọn câu đúng.
Đáp án : A
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên câu A đúng, câu C sai.
+ Hai tam giác đồng dạng thì chưa chắc bằng nhau nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1 nên câu B sai.
+ Hai tam giác vuông chưa chắc đồng dạng (chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau) nên câu D sai.
Câu 7 : Hãy chọn câu sai.
Đáp án : C
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên A đúng.
+ Hai tam giác đều có các góc đều bằng 600 và các cạnh của mỗi tam giác bằng nhau nên các cạnh tương ứng tỉ lệ . Vậy hai tam giác đều luôn đồng dạng nên B đúng.
+ Hai tam giác cân chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau nên không đồng dạng nên C sai
+ Câu D đúng vì là định nghĩa hai tam giác đồng dạng.
Câu 8 : Cho ΔABC,ΔMNP nếu có ˆA=ˆM;ˆB=ˆN;ˆC=ˆP để ΔABC∽ΔMNP theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
Đáp án : A
ΔABC∽ΔMNP⇔{ABMN=ACMP=BCNPˆA=ˆM;ˆB=ˆN;ˆC=ˆP
Mà ˆA=ˆM;ˆB=ˆN;ˆC=ˆP(gt)
nên cần bổ sung thêm điều kiện ABMN=ACMP=BCNP thì ΔABC∽ΔMNP (định nghĩa).
Câu 9 : Cho ΔABC∽ΔMNP theo tỉ số 2. Khẳng định nào sau đây là đúng
Đáp án : D
Vì ΔABC∽ΔMNP theo tỉ số 2 (gt) ⇒BC=2NP
Câu 10 : Hãy chọn câu đúng
Nếu ΔABC∽ΔMNP theo tỉ số k=23 thì ΔMNP∽ΔABC theo tỉ số
Đáp án : B
Vì ΔABC∽ΔMNP theo tỉ số đồng dạng là k=23 ⇒ΔMNP∽ΔABC theo tỉ số đồng dạng là 1k=32
Câu 11 : Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.
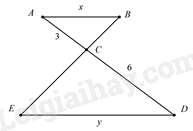
Đáp án : D
Vì AB // DE ⇒ΔABC∽ΔDEC (định lí)
⇒ABDE=ACCD (các cạnh tương ứng) ⇒xy=35=12
Câu 12 : Cho ΔABC∽ΔA1B1C1 theo tỉ số 2:3 và ΔA1B1C1∽ΔA2B2C2 theo tỉ số 1 :3. Vậy ΔABC∽ΔA2B2C2 theo tỉ số k bằng
Đáp án : B
Vì ΔABC∽ΔA1B1C1 theo tỉ số 2:3⇒ABA1B1=23
Vì ΔA1B1C1∽ΔA2B2C2 theo tỉ số 1:3⇒A1B1A2B2=13
⇒ABA2B2=ABA1B1.A1B1A2B2=23.13=29
Vậy ΔABC∽ΔA2B2C2 theo tỉ số k=2:9 .
Câu 13 : Cho ΔA1B1C1∽ΔABC theo tỉ số đồng dạng k=23 . Tỉ số chu vi của hai tam giác đó là:
Đáp án : D
Vì ΔA1B1C1∽ΔABC theo tỉ số đồng dạng k=23 .
⇒A1B1AB=A1C1AC=B1C1BC=A1B1+A1C1+B1C1AB+AC+BC=23⇒CVΔA1B1C1CVΔABC=23
Hai tam giác đồng dạng theo tỉ số nào thì chu vi cũng đồng dạng theo tỉ số đó.
Câu 14 : Nếu ΔA1B1C1 đồng dạng với ΔABC theo tỉ số 4 thì tỉ số chu vi của ΔA1B1C1 và ΔABC là
Đáp án : A
Vì ΔA1B1C1 đồng dạng với ΔABC theo tỉ số 4
⇒A1B1AB=A1C1AC=B1C1BC=A1B1+A1C1+B1C1AB+AC+BC=4⇒CVΔA1B1C1CVΔABC=4
Câu 15 : ΔABC∽ΔDEF theo tỉ số k=23 , biết ΔABC có chu vi bằng 42cm. Chu vi ΔDEF là:
Đáp án : A
Vì ΔABC∽ΔDEF theo tỉ số
k=32⇒ABDE=ACDF=BCEF=AB+AC+BCDE+FD+EF=32⇒CVΔABCCVΔEFD=32⇒42CVΔDEF=32⇒CVΔEFD=42.23=28(cm)
Câu 16 : Cho ΔMNI∽ΔABC theo tỉ số k=57 và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
Đáp án : D
Vì ΔMNI∽ΔABC theo tỉ số k=57
⇒MNAB=MIAC=NIBC=MN+MI+NIAB+AC+BC=57⇒CVΔMNICVΔABC=57⇒CVΔMNICVΔABC−CVΔMNI=57−5⇒CVΔMNI16=52⇒CVΔMNI=16.52=40(cm).⇒CVΔABC=40+16=56(cm).
Câu 17 : Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
(I)ΔAME∽ΔADC , tỉ số đồng dạng k1=13
(II)ΔCBA∽ΔADC , tỉ số đồng dạng k2=1
(III)ΔCNE∽ΔADC , tỉ số đồng dạng k3=23
Chọn câu đúng:
Đáp án : C
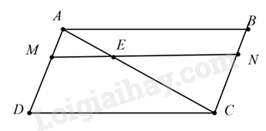
Xét ΔADC có ME//CD (gt) ⇒ΔAME∽ΔADC(1) theo tỉ số đồng dạng k1=AEAC=13
Vì ABCD là hình bình hành nên
+ ⌢B=⌢D
+ AB//CD⇒^BAC=^ACD (so le trong)
+ AD//BC⇒^ACB=^CAD (so le trong)
+ AD = BC ; AB = CD
Xét ΔCBA và ΔADC có :
+ ⌢B=⌢D;^BAC=^ACD;^ACB=^CAD(cmt)
+ ABCD=BCAD=ACAC(=1)
⇒ΔCBA∽ΔADC theo tỉ lệ đồng dạng k2=1
Xét ΔABC có :
EN//CD (gt) mà AB//CD (cmt)
⇒EN//AB⇒ΔCNE∽ΔCBA
Mà ΔCBA∽ΔADC(cmt)
⇒ΔCNE∽ΔADC theo tỉ lệ đồng dạng k3=CEAC=23 (Vì AC=3AE⇒CE=23AC)
Vậy khẳng định (I), (II), (III) đều đúng.
Câu 18 : Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm I sao cho AC=32AI . Qua I vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
(I)ΔAMI∽ΔADC tỉ số đồng dạng k1=23
(II)ΔCBA∽ΔADC , tỉ số đồng dạng k2=1
(III)ΔCNI∽ΔADC , tỉ số đồng dạng k3=23 .
Số khẳng định đúng là:
Đáp án : B
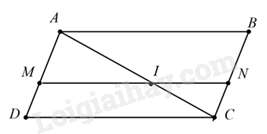
Xét tam giác ADC có MI//CD⇒ΔAMI∽ΔADC(1) theo tỉ số đồng dạng k1=AIAC=23
Vì ABCD là hình bình hành nên:
+ ˆB=ˆD
+ AB//CD⇒^BAC=^ACD (so le trong)
+ AD//BC⇒^ACB=^CAD (so le trong)
+ AD = BC; AB = DC
Xét ΔCBA và ΔADC có :
+ˆB=ˆD;^BAC=^ACD;^ACB=^CAD
+ ABCD=BCAD=ACAC(=1)
⇒ΔCBA∽ΔADC theo tỉ số đồng dạng k2=1
Xét ΔADC có IN // CD (gt) mà AB // CD (cmt)
⇒IN//AB⇒ΔCNI∽ΔCBA
Mà ΔCBA∽ΔADC (cmt)
⇒ΔCNI∽ΔADC theo tỉ số đồng dạng k3=CIAC=13 .
Vậy có 2 khẳng định (I), (II) đúng.
Câu 19 : Cho tam giác ABC , lấy M trên cạnh BC sao cho MBMC=12 Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
Đáp án : A
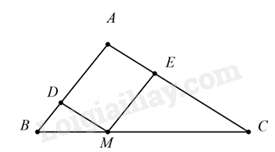
Vì MD // AC ⇒ΔDBM∽ΔABC
Vì ME // AB ⇒ΔEMC∽ΔABC
⇒ΔDBM∽ΔEMC(∽ΔABC)
⇒DBEM=DMEC=BMMC=DB+DM+BMEM+EC+MC=12CVΔDBMCVΔEMC=12
Mà chu vi tam giác MEC bằng 24 cm
Chu vi tam giác DBM bằng 24 : 2 = 12 (cm).
Câu 20 : Cho tam giác ABC , lấy E trên cạnh BC sao cho EBEC=23 Qua E kẻ đường thẳng song song với AC cắt AB tại I và đường thẳng song song với AB cắt AC tại K , biết hiệu chu vi tam giác EKC và chu vi tam giác BEI bằng 24 cm thì chu vi tam giác BEI là
Đáp án : C
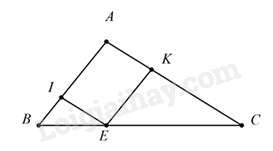
Vì EI // AC ⇒ΔIBE∽ΔABC
Vì EI // AB ⇒ΔKEC∽ΔABC
⇒ΔIBE∽ΔKEC(∽ΔABC)
⇒IBKE=IEKC=BEEC=IB+IE+BEKE+KC+EC=23CVΔIBECVΔKEC=23⇒CVΔIBECVΔKEC−CVΔIBE=23−2⇒CVΔIBE24=21
Chu vi của tam giác IBE bằng 24. 2 = 48 cm
Xem thêm các bài giải Trắc nghiệm Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
