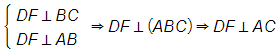Với lời giải SBT Toán 11 trang 76 Tập 2 chi tiết trong Bài tập cuối chương 8 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài tập cuối chương 8
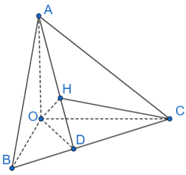
Bài 1 trang 76 SBT Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Chứng minh rằng:
a) BC ⊥ (OAH).
b) H là trực tâm của ∆ABC.
c) .
Lời giải:
a)Ta có: 
Từ (1) và (2) BC ⊥ (OAH).
b)Từ a) BC ⊥ AH. (*)
Ta dễ dàng chứng minh được OC ⊥ (OAB) OC ⊥ AB. (3)
Lại có: OH ⊥ AB (do OH ⊥ (ABC)) OH ⊥ AB. (4)
Từ (3) và (4) AB ⊥ (OHC) hay AB ⊥ HC. (**)
Từ (*) và (**) H là trực tâm của tam giác ABC.
c)Dễ thấy OD, OH là các đường cao của tam giác OBC và OAD.
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
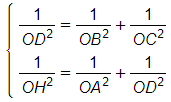
Do đó
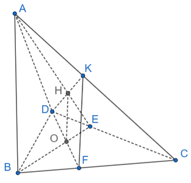
Bài 2 trang 76 SBT Toán 11 Tập 2: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Vẽ các đường cao BE, DF của tam giác BCD, đường cao DK của tam giác ACD.
a) Chứng minh hai mặt phẳng (ABE) và (DFK) cùng vuông góc với (ADC).
b) Gọi O và H là trực tâm ∆BCD và ∆ACD. Chứng minh OH vuông góc với (ADC).
Lời giải:
a)Từ giả thiết suy ra AB ⊥ (BDC) AB ⊥ DC.
Lại có: BE ⊥ DC.
DC ⊥ (ABE) hay (ADC) ⊥ (ABE). (1)
Ta có: 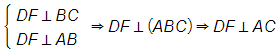 .
.
Mà DK ⊥ AC.
Do đó AC ⊥ (DFK) hay (ADC) ⊥ (DFK). (2)
b)Dễ thấy O, H lần lượt là các giao điểm của DF và BE, AE và DK.
(ABE) (DFK) = OH. (3)
Từ (1), (2) và (3) OH ⊥ (ADC).
Bài 3 trang 76 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tỉnh khoảng cách giữa hai đường thẳng SA và BC theo a.
Lời giải:
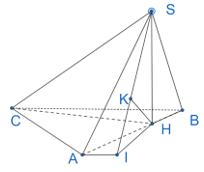
Qua A kẻ đường thẳng song song với BC, I là hình chiếu của H trên đường thẳng đó.
Ta có BC // (SAI)
Suy ra d(BC, SA) = d(BC, (SAI))
= d(B, (SAI)) = .
Gọi K là hình chiếu của H trên SI.
Dễ dàng chứng minh được AI ⊥ (SHI) AI ⊥ HK.
HK ⊥ (SAI) d(H, (SAI)) = HK.
Tam giác AIH vuông tại I:
Tam giác SHC vuông tại H:
Tam giác SHI vuông tại H:
Bài 4 trang 76 SBT Toán 11 Tập 2: Cho khối chóp tam giác S.ABC có SA ⊥ (ABC), tam giác ABC có độ dài 3 cạnh là AB = 5a, BC = 8a, AC = 7a, góc giữa SB và (ABC) là 45°. Tính thể tích khối chóp S.ABC.
Lời giải:
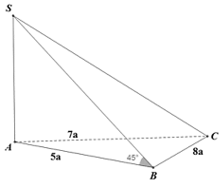
Ta có:
Áp dụng định lí Heron
Bài 5 trang 76 SBT Toán 11 Tập 2: Cho hình lăng trụ đứng có đáy ABC là tam giác vuông tại B. Biết AB = a, BC = , góc giữa hai mặt phẳng () và (ABC) bằng 60°.
Tính .
Lời giải:
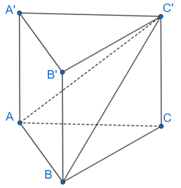
Ta có:
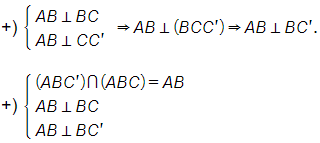
Bài 6 trang 76 SBT Toán 11 Tập 2: Cho khối lăng trụ đứng có đáy ABC là tam giác cân với AB = AC = a, , mặt phẳng (AB'C') tạo với đáy một góc 60°. Tính thể tích V của khối lăng trụ đã cho.
Lời giải:
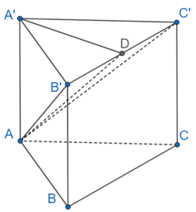
Cho D là trung điểm của B'C'.
Đáy A'B'C' cân tại A' nên A'D ⊥ B'C'.
Mà AA' ⊥ B'C' nên B'C' ⊥ (ADA').
B'C' ⊥ AD.
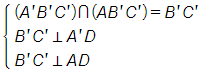
.
Bài 7 trang 76 SBT Toán 11 Tập 2: Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B'AC) tạo với đáy một góc 30°, khoảng cách từ B đến mặt phẳng (D'AC) bằng . Tính thể tích khối tứ diện ACB'D'.
Lời giải:
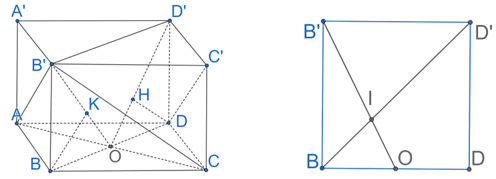
Gọi O = AC BD. Ta có:
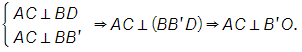
Khi đó:
Dễ thấy .
Từ D kẻ DH ⊥ D'O (H ϵ DO), suy ra
Xét ∆B'BO:
Xét ∆D'DO:
Gọi I = BD B'O, suy ra
Mà
Suy ra
Vậy
Bài 8 trang 76 SBT Toán 11 Tập 2: Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60 cm và 120 cm, cạnh bên của thùng dài 100 cm. Tính thể tích của thùng.
Lời giải:
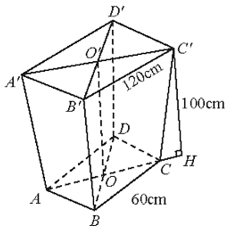
Kẻ C'H ⊥ AC (H ϵ AC).
Ta có 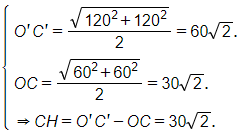
Áp dụng công thức:
Với 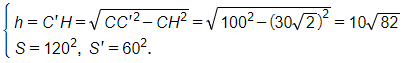
Ta có:
Vậy thể tích của thùng
Xem thêm lời bài sách bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Câu 1 trang 74 SBT Toán 11 Tập 2: Trong không gian, khẳng định nào sau đây đúng?...
Câu 2 trang 74 SBT Toán 11 Tập 2: Khẳng định nào sau đây sai?..
Câu 3 trang 74 SBT Toán 11 Tập 2: Cho tứ diện ABCD. Vẽ AH ⊥ (BCD). Biết H là trực tâm tam giác BCD. Khẳng định nào sau đây đúng?....
Câu 4 trang 74 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Gọi E, F lần lượt là hình chiếu của A lên SB, SD. Khẳng định nào sau đây sai?....
Câu 5 trang 74 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD đáy là hình vuông cạnh a, tâm O. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi α là góc tạo bởi đường thẳng SC và mặt phẳng đáy. Khẳng định nào sau đây đúng?...
Câu 6 trang 74 SBT Toán 11 Tập 2: Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?...
Câu 7 trang 75 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB = . Biết SA ⊥ (ABC) và SA = a. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng...
Câu 8 trang 75 SBT Toán 11 Tập 2: Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì...
Câu 9 trang 75 SBT Toán 11 Tập 2: Cho hình lăng trụ tam giác đều có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng () bằng....
Câu 10 trang 75 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng BE và SC....
Câu 11 trang 75 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 2a, AD = a. Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45°. Khi đó thể tích khối chóp S.ABCD là...
Câu 12 trang 75 SBT Toán 11 Tập 2: Cho khối chóp S.ABCD có đáy là hình chữ nhật AB = a, AD = , SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc 30°. Tính thể tích V của khối chóp đã cho....
Câu 13 trang 75 SBT Toán 11 Tập 2: Cho lăng trụ đứng ABC A'B'C' có đáy tam giác ABC vuông tại B, AB = 2a, BC = a, . Thể tích khối lăng trụ ABC.A'B'C' là....
Câu 14 trang 75 SBT Toán 11 Tập 2: Gọi V là thể tích của hình lập phương . V1 là thể tích của tử diện Hệ thức nào sau đây là đúng?...
Bài 1 trang 76 SBT Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Chứng minh rằng:....
Bài 2 trang 76 SBT Toán 11 Tập 2: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Vẽ các đường cao BE, DF của tam giác BCD, đường cao DK của tam giác ACD....
Bài 3 trang 76 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tỉnh khoảng cách giữa hai đường thẳng SA và BC theo a....
Bài 4 trang 76 SBT Toán 11 Tập 2: Cho khối chóp tam giác S.ABC có SA ⊥ (ABC), tam giác ABC có độ dài 3 cạnh là AB = 5a, BC = 8a, AC = 7a, góc giữa SB và (ABC) là 45°. Tính thể tích khối chóp S.ABC.....
Bài 5 trang 76 SBT Toán 11 Tập 2: Cho hình lăng trụ đứng có đáy ABC là tam giác vuông tại B. Biết AB = a, BC = , góc giữa hai mặt phẳng () và (ABC) bằng 60°....
Bài 6 trang 76 SBT Toán 11 Tập 2: Cho khối lăng trụ đứng có đáy ABC là tam giác cân với AB = AC = a, , mặt phẳng (AB'C') tạo với đáy một góc 60°. Tính thể tích V của khối lăng trụ đã cho.....
Bài 7 trang 76 SBT Toán 11 Tập 2: Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B'AC) tạo với đáy một góc 30°, khoảng cách từ B đến mặt phẳng (D'AC) bằng . Tính thể tích khối tứ diện ACB'D'.....
Bài 8 trang 76 SBT Toán 11 Tập 2: Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60 cm và 120 cm, cạnh bên của thùng dài 100 cm. Tính thể tích của thùng.....
Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác: