Giải SBT Toán 8 trang 63 Tập 1 Cánh diều

Nguyễn Mạnh Tài Ngày: 16-11-2023 Lớp 8

651

Với lời giải SBT Toán 8 trang 63 Tập 1 Bài tập cuối chương 3 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 3

Bài 28 trang 63 SBT Toán 8 Tập 1: Tọa độ giao điểm của hai đường thẳng $d_{1} : y = \frac{1 - 3 x}{4}$ và $d_{2} : y = - (\frac{x}{3} + 1)$ là:
A. $(0; - 1)$
B. $(- \frac{7}{3}; 2)$
C. $(0; \frac{1}{4})$
D. $(3; - 2)$

Lời giải:

Ta có: $d_{1} : y = \frac{1 - 3 x}{4} = - \frac{3}{4} x + \frac{1}{4}$

$d_{2} : y = - (\frac{x}{3} + 1) = - \frac{1}{3} x - 1$

Xét đồ thị hàm số $d_{1} : y = \frac{- 3}{4} x + \frac{1}{4}$

Chọn $x = 0$ suy ra $y = \frac{1}{4}$

Chọn $y = 0$ suy ra $x = \frac{1}{3}$

Vậy đồ thị hàm số $d_{1} : y = \frac{- 3}{4} x + \frac{1}{4}$ là đường thẳng đi qua hai điểm $A (0; \frac{1}{4}), B (\frac{1}{3}; 0)$

Xét đồ thị hàm số $d_{2} : y = - \frac{1}{3} x - 1$

Chọn $x = 0$ suy ra $y = - 1$

Chọn $y = 0$ suy ra $x = - 3$

Vậy đồ thị hàm số $d_{2} : y = - \frac{1}{3} x - 1$ là đường thẳng đi qua hai điểm $C (0; - 1), D (- 3; 0)$

Vẽ trên mặt phẳng tọa độ $O x y$ :

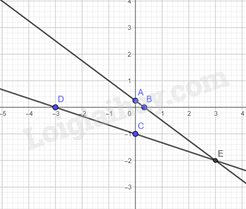
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 3 (ảnh 1)

Ta xác định được giao điểm $E (3; - 2)$ .

→ Đáp án D.

Bài 29 trang 63 SBT Toán 8 Tập 1: Cho đồ thị của hàm số $y = a x + b$ đi qua điểm $M (1; 4)$ và song song với đường thẳng $y = 2 x + 1$ . Tích $a b$ bằng:

A. 6

B. 4

C. 3

D. 2

Lời giải:

Đồ thị của hàm số $y = a x + b$ song song với đường thẳng $y = 2 x + 1$ nên $a = 2$ và $b \neq 1$ .

Đồ thị của hàm số $y = 2 x + b$ đi qua điểm $M (1; 4)$ nên $4 = 2.1 + b$ suy ra $b = 2$

Vậy $a . b = 2.2 = 4$

→ Đáp án B.

Bài 30 trang 63 SBT Toán 8 Tập 1: Trong mặt phẳng tọa độ $O x y$ , cho đồ thị của hàm số $y = 2 x + 4$ (Hình 11).

a) Gọi $A, B$ lần lượt là giao điểm của trục $O x, O y$ với đồ thị hàm số $y = 2 x + 4$ . Xác định tọa độ các điểm $A, B$ .

b) Gọi $M, N$ lần lượt là trung điểm của $O A, O B$ . Xác định tọa độ các điểm $M, N$ .

c) Tính tỉ số phần trăm của diện tích tam giác $O M N$ và diện tích tam giác $O A B$ .

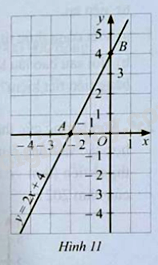
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 3 (ảnh 2)

Lời giải:

a) Tọa độ điểm $A (- 2; 0)$

Tọa độ điểm $B (0; 4)$

b) Ta vẽ các điểm $M, N$ :

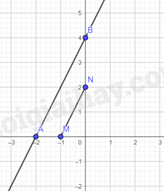
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 3 (ảnh 3)

Vậy tọa độ điểm $M (- 1; 0), N (0; 2)$ .

c) Diện tích của tam giác $O A B$ bằng: $\frac{1}{2} . O A . O B$

Mà $O M = \frac{1}{2} O A, O N = \frac{1}{2} O B$ nên ta có diện tích của tam giác $O M N$ bằng:

$\frac{1}{2} . \frac{1}{2} O A . \frac{1}{2} O B = \frac{1}{4} . \frac{1}{2} . O A . O B$

Vậy tỉ số phần trăm của diện tích tam giác $O M N$ và diện tích tam giác $O A B$ là:

$\frac{1}{4} .100 % = 25 %$

Bài 31 trang 63 SBT Toán 8 Tập 1: Trong mặt phẳng tọa độ $O x y$ , cho các điểm $A (2; 3), B (2; - 4)$ . Tìm tọa độ điểm $C$ sao cho $C$ nằm trên trục $O x$ và $C A + C B$ đạt giá trị nhỏ nhất.

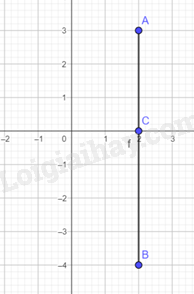
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 3 (ảnh 4)

Lời giải:

Ta có: $C A + C B \geq A B$ nên $C A + C B$ đạt giá trị nhỏ nhất bằng $A B = 7$ . Khi đó, $C$ là giao điểm của $A B$ và trục $O x$ . Vậy $C (2; 0)$ .

Bài 32 trang 63 SBT Toán 8 Tập 1: Cho đường thẳng $d : y = (m - \frac{1}{2}) x + 2 m - 2$ với $m \neq \frac{1}{2}$ . Tìm giá trị của $m$ để:

a) Đường thẳng $d$ song song với đường thẳng $d_{1} : y = \frac{1}{2} m x - 2$ với $m \neq 0$ ;

b) Đường thẳng $d$ trùng với đường thẳng $d_{2} : y = x - \frac{2}{3} m + 2$ ;

c) Đường thẳng $d$ và đường thẳng $d_{3} : y = \sqrt{2} x - m + 2$ cắt nhau tại một điểm nằm trên trục $O y$ .

Lời giải:

a) Để $d$ song song với $d_{1}$ thì $m - \frac{1}{2} = \frac{1}{2} m$ và $2 m - 2 \neq - 2$ . Suy ra $m = 1$ .

Dễ thấy với $m = 1$ ta có $d$ và $d_{1}$ trở thành $d : y = \frac{1}{2} x$ và $d_{1} : y = \frac{1}{2} x - 2$ . Khi đó, $d$ song song với $d_{1}$ .

b) Để $d$ trùng với $d_{1}$ thì $m - \frac{1}{2} = 1$ và $2 m - 2 = - \frac{2}{3} m + 2$ . Suy ra $m = \frac{3}{2}$ .

c) Đường thẳng $d$ và đường thẳng $d_{3}$ lần lượt cắt trục $O y$ tại $A (; 2 m - 2)$ và $B (0; - m + 2)$ . Do đó, $d$ và $d_{3}$ cắt nhau tại một điểm nằm trên trục $O y$ khi $m - \frac{1}{2} \neq \sqrt{2}$ và $2 m - 2 = - m + 2$ . Suy ra $m = \frac{4}{3}$ .

Dễ thấy với $m = \frac{4}{3}$ ta có $d$ và $d_{3}$ trở thành $d : y = \frac{5}{6} x + \frac{2}{3}$ và $d_{3} : y = \sqrt{2} x + \frac{2}{3}$

Khi đó $d$ và $d_{3}$ cắt nhau tại điểm $(0; \frac{2}{3})$ nằm trên trục $O y$

Bài 33 trang 63 SBT Toán 8 Tập 1: Xác định đường thẳng $d : y = a x + b (a \neq 0)$ trong mỗi trường hợp sau:

a) Đường thẳng $d$ song song với đường thẳng $d^{'} : y = - 3 x - \frac{2}{3}$ và đi qua điểm $A (- 2; - 4)$ .

b) Đường thẳng $d$ đi qua điểm $B$ và có hệ số góc bằng -3. Biết $B$ là giao điểm của đường thẳng $y = 2 x - 2$ với trục hoành.

Lời giải:

a) Để đường thẳng $d$ song song với đường thẳng $d^{'} : y = - 3 x - \frac{2}{3}$ thì $a = a^{'}$ vậy đồ thị hàm số của đường thẳng $d : y = - 3 x + b$ .