Cho hai hàm số f(x) = 3x^3 ‒ 3x^2 + 6x ‒ 1 và g(x) = x^3 + x^2 ‒ 2

Cho hai hàm số f(x) = 3x^3 ‒ 3x^2 + 6x ‒ 1 và g(x) = x^3 + x^2 ‒ 2

Van Anh Ngày: 15-11-2023 Lớp 11

213

Với giải Câu 3 trang 44 SBT Toán lớp 11 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài tập cuối chương 7

Câu 3 trang 44 SBT Toán 11 Tập 2: Cho hai hàm số f(x) = 3x³ ‒ 3x² + 6x ‒ 1 và g(x) = x³ + x² ‒ 2. Bất phương trình $f^{''} (x) - f^{'} (x) + g^{'} (x) - 8 \geq 0$ có tập nghiệm là

A. $(1; \frac{10}{3})$ .

Cho hai hàm số fx = 3x^3 ‒ 3x^2 + 6x ‒ 1 và gx = x^3 + x^2 ‒ 2 Bất phương trình

D. $(- \infty; 1) \cup (\frac{10}{3}; + \infty)$ .

Lời giải:

Đáp án đúng là: C

Ta có:

• $f^{'} (x) = 9 x^{2} - 6 x + 6$

• $f^{''} (x) = 18 x - 6$

• $g^{'} (x) = 3 x^{2} + 2 x$

Từ đó $f^{''} (x) - f^{'} (x) + g^{'} (x) - 8 \geq 0$

$\begin{matrix} \Leftrightarrow 18 x - 6 - (9 x^{2} - 6 x + 6) + 3 x^{2} + 2 x - 8 \geq 0 \\ \Leftrightarrow - 6 x^{2} + 26 x - 20 \geq 0 \\ \Leftrightarrow 1 \leq x \leq \frac{10}{3} \end{matrix}$

Vậy bất phương trình $f^{''} (x) - f^{'} (x) + g^{'} (x) - 8 \geq 0$ có tập nghiệm là 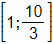Cho hai hàm số fx = 3x^3 ‒ 3x^2 + 6x ‒ 1 và gx = x^3 + x^2 ‒ 2 Bất phương trình .

Xem thêm lời bài sách bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Câu 1 trang 44 SBT Toán 11 Tập 2: Cho hàm số y = x³ + 3x² ‒ 2. Tiếp tuyến với đồ thị của hàm số tại điểm M(‒1; ‒6) có hệ số góc bằng:...

Câu 2 trang 44 SBT Toán 11 Tập 2: Hàm số y = x³ ‒ 3x + 1 có đạo hàm tại x = ‒1 bằng.....

Câu 3 trang 44 SBT Toán 11 Tập 2: Cho hai hàm số f(x) = 3x³ ‒ 3x² + 6x ‒ 1 và g(x) = x³ + x² ‒ 2. Bất phương trình $f^{''} (x) - f^{'} (x) + g^{'} (x) - 8 \geq 0$ có tập nghiệm là...

Câu 4 trang 44 SBT Toán 11 Tập 2: Hàm số $y = \frac{2 x - 1}{3 x + 2}$ có đạo hàm là...

Câu 5 trang 44 SBT Toán 11 Tập 2: Hàm số $y = \frac{x - 1}{x + 1}$ có đạo hàm cấp hai tại x = 1 là...

Câu 6 trang 44 SBT Toán 11 Tập 2: Hàm số $y = 3^{x^{2} + 1}$ có đạo hàm là..

Câu 7 trang 45 SBT Toán 11 Tập 2: Hàm số y = ln (cos x) có đạo hàm là....

Câu 8 trang 45 SBT Toán 11 Tập 2: Hàm số $f (x) = e^{\sqrt{x^{2} + 4}}$ có đạo hàm tại x = 1 bằng.....

Bài 1 trang 45 SBT Toán 11 Tập 2: Dùng định nghĩa để tính đạo hàm của các hàm số sau:..

Bài 2 trang 45 SBT Toán 11 Tập 2: Cho hàm số f(x) = 2x³ – x² + 2x +1 có đồ thị (C). Tìm tiếp tuyến với (C) có hệ số góc nhỏ nhất....

Bài 3 trang 45 SBT Toán 11 Tập 2: Vị trí chuyển động của một vật trên đường thẳng được biểu diễn bởi công thức $s (t) = 3 t^{3} + 5 t + 2$ , trong đó t là thời gian tính bằng giây và s tính bằng mét. Tính vận tốc và gia tốc của vật đó khi t = 1....

Bài 4 trang 45 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:...

Bài 5 trang 45 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:..

Bài 6 trang 45 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau biết rằng f và g là các hàm số có đạo hàm trên ℝ:...

Bài 7 trang 45 SBT Toán 11 Tập 2: Cho hàm số $f (x) = x^{3} + 2 x^{2} - m x - 5$ . Tìm m để...

Bài 8 trang 45 SBT Toán 11 Tập 2: Cho hàm số $f (x) = \sqrt{x^{2} - 2 x + 8}$ . Giải phương trình $f^{'} (x) = - \frac{2}{3}$ ....

Bài 9 trang 45 SBT Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:....

Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Các quy tắc tính đạo hàm

Bài tập cuối chương 7

Bài 1: Hai đường thẳng vuông góc

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Hai mặt phẳng vuông góc

Bài 4: Khoảng cách trong không gian

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

363

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

280

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

225

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

242

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.