Với giải sách bài tập Toán 10 Bài 4: Bất phương trình bậc nhất một ẩn sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 4: Bất phương trình bậc nhất một ẩn
Giải SBT Toán 10 trang 56 Tập 1
A. – 2x2 + 3x < 0;
B. 0,5y2 – (y – 2) ≤ 0;
C. x2 – 2xy – 3 ≥ 0;
D. x2 – 3 ≥ 0.
Lời giải
Đáp án đúng là C
Xét bất phương trình – 2x2 + 3x < 0 là bất phương trình bậc hai một ẩn x. Do đó A sai.
Xét bất phương trình 0,5y2 – (y – 2) ≤ 0 ⇔ 0,5y2 – y + 2 ≤ 0 là bất phương trình bậc hai một ẩn y. Do đó B sai.
Xét bất phương trình x2 – 2xy – 3 ≥ 0 là bất phương trình bậc hai nhưng lại có hai ẩn x và y. Do đó C đúng.
Xét bất phương trình x2 – 3 ≥ 0 là bất phương trình bậc hai một ẩn x. Do đó D sai.
Bài 29 trang 56 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình – x2 + 3x + 18 ≥ 0 là:
A. [ – 3; 6];
B. (– 3; 6);
C. (– ∞; – 3) ∪ (6; +∞);
D. (– ∞; – 3] ∪ [6; +∞).
Lời giải
Đáp án đúng là A
Xét f(x) = – x2 + 3x + 18 là một tam thức bậc hai có a = – 1 < 0 và ∆ = 32 – 4.(– 1).18 = 81 > 0.
Do đó f(x) có hai nghiệm phân biệt là x1 = – 3 và x2 = 6.
Theo định lí về dấu tam thức bậc hai, ta có:
f(x) > 0 khi x ∈ (– 3; 6);
f(x) < 0 khi x ∈ (–∞; – 3) ∪ (6; +∞);
Suy ra f(x) ≥ 0 khi x ∈ [– 3; 6].
Vậy tập nghiệm của bất phương trình là S = [– 3; 6].
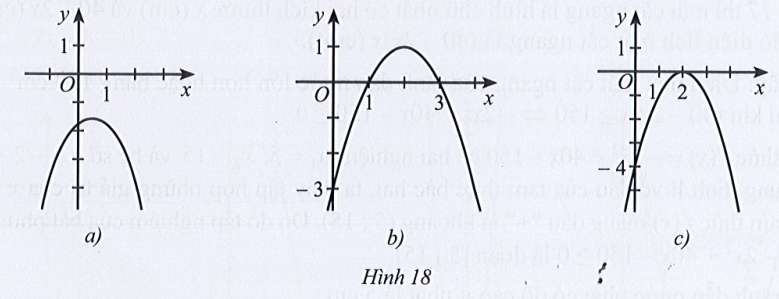
Lời giải
+) Hình 18a):
Quan sát đồ thị hàm số, ta thấy:
Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành với mọi x ∈ ℝ.
Do đó:
f(x) < 0 và f(x) ≤ 0 luôn đúng với mọi x ∈ ℝ.
f(x) > 0; f(x) ≥ 0 và vô nghiệm.
Vậy tập nghiệm của các bất phương trình f(x) > 0 và f(x) ≥ 0 là , tập nghiệm của bất phương trình f(x) < 0 và f(x) ≤ 0 là ℝ.
+) Hình 18b):
Quan sát đồ thị hàm số, ta thấy:
Với x ∈ (1; 3) hàm số nằm trên trục hoành hay f(x) > 0.
Với x < 1 hoặc x > 3 đồ thị hàm số nằm phía dưới trục hoành hay f(x) < 0.
Đồ thị hàm số cắt trục hoành tại x = 1 hoặc x = 3.
Do đó:
f(x) > 0 khi x ∈ (1; 3).
f(x) < 0 khi x ∈ (– ∞; 1) ∪ (3; +∞).
f(x) ≥ 0 khi x ∈ [1; 3].
f(x) ≤ 0 khi x ∈ (– ∞; 1] ∪ [3; +∞).
Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là (1; 3); (– ∞; 1) ∪ (3; +∞); [1; 3]; (– ∞; 1] ∪ [3; +∞).
+) Hình 18c):
Quan sát đồ thị hàm số, ta thấy:
Đồ thị hàm số cắt trục hoành tại x = 2.
Với x ≠ 2 hàm số nằm dưới trục hoành hay f(x) < 0.
Do đó:
f(x) > 0 vô nghiệm.
f(x) < 0 khi x ∈ ℝ \ {2}.
f(x) ≥ 0 khi x = 2.
f(x) ≤ 0 khi x ∈ ℝ.
Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là ; ℝ \ {2}; {2}; ℝ.
Bài 31 trang 56 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:
a) 3x2 – 8x + 5 > 0;
Lời giải
a) Xét tam thức bậc hai f(x) = 3x2 – 8x + 5, có a = 3, ∆ = (– 8)2 – 4.3.5 = 4 > 0
Suy ra tam thức bậc hai có hai nghiệm x1 = 1 và x2 =.
Áp dụng định lí dấu của tam thức bậc hai, ta có:
f(x) > 0 khi x ∈ ;
f(x) < 0 khi x ∈ .
Suy ra 3x2 – 8x + 5 > 0 khi x ∈ .
Vậy tập nghiệm của bất phương trình 3x2 – 8x + 5 > 0 là .
b) Xét tam thức bậc hai g(x) = – 2x2 – x + 3, có a = – 2 < 0 và ∆ = (– 1)2 – 4.(– 2).3 = 25 > 0.
Do đó tam thức có hai nghiệm phân biệt x1 = 1 và x2 =.
Áp dụng định lí về dấu của tam thức bậc hai ta có:
g(x) > 0 khi x ∈ ;
g(x) < 0 khi x ∈ .
Suy ra – 2x2 – x + 3 ≤ 0 khi x ∈ .
Vậy tập nghiệm của bất phương trình đã cho là S = .
c) Xét tam thức bậc hai h(x) = 25x2 – 10x + 1, có a = 25 > 0 và ∆ = (– 10)2 – 4.25.1 = 0.
Do đó tam thức có nghiệm kép là x = .
Áp dụng định lí về dấu của tam thức bậc hai ta có:
h(x) > 0 khi x ≠ .
Suy ra 25x2 – 10x + 1 < 0 khi x ∈ .
Vậy tập nghiệm của bất phương trình đã cho là S = .
d) Xét tam thức bậc hai k(x) = – 4x2 + 5x + 9 , có a = – 4 < 0 và ∆ = 52 – 4.(– 4).9 = 169 > 0.
Do đó tam thức có hai nghiệm phân biệt là x1 = – 1 và x2 = .
Áp dụng định lí về dấu của tam thức bậc hai ta có:
k(x) < 0 khi x ∈ ;
k(x) > 0 khi x ∈ .
Suy ra – 4x2 + 5x + 9 ≥ 0 khi x ∈ .
Vậy tập nghiệm của bất phương trình đã cho là S = .
Giải SBT Toán 10 trang 57 Tập 1
Lời giải
Xét tam thức bậc hai f(x) = – 3x2 + 7x + 10, có a = – 3 < 0 và ∆ = 72 – 4.(– 3).10 = 169 > 0.
Do đó tam thức có hai nghiệm phân biệt là x1 = – 1 và x2 = .
Áp dụng định lí về dấu của tam thức bậc hai ta có:
f(x) < 0 khi x ∈ ;
f(x) > 0 khi x ∈ .
Suy ra tập nghiệm của bất phương trình – 3x2 + 7x + 10 ≥ 0 là S1 = .
Xét tam thức bậc hai g(x) = – 2x2 – 9x + 11, có a = – 2 < 0 và ∆ = (– 9)2 – 4.(– 2).11 = 169 > 0.
Do đó tam thức có hai nghiệm phân biệt là x1 = 1 và x2 = .
Áp dụng định lí về dấu của tam thức bậc hai ta có:
g(x) < 0 khi x ∈ ;
g(x) > 0 khi x ∈ .
Suy ra tập nghiệm của bất phương trình – 2x2 – 9x + 11 > 0 là S2 = .
Đặt S = S1 ∩ S2 = .
Ta có hình vẽ sau:

Vậy giao của hai tập nghiệm của hai bất phương trình trên là S = [ – 1; 1).
Bài 33 trang 57 SBT Toán 10 Tập 1: Tìm m để phương trình – x2 + (m + 2)x + 2m – 10 = 0 có nghiệm.
Lời giải
Xét phương trình – x2 + (m + 2)x + 2m – 10 = 0 có ∆ = (m + 2)2 – 4.(– 1).(2m – 10) = m2 + 12m – 36.
Để phương trình đã cho có nghiệm thì ∆ ≥ 0 ⇔ m2 + 12m – 36 ≥ 0
Xét tam thức bậc hai f(m) = m2 + 12m – 36, có a = 1, ∆m = 122 – 4.1.(– 36) = 288 > 0.
Do đó tam thức có hai nghiệm phân biệt m1 = và m1 = .
Áp dụng định lí về dấu của tam thức bậc hai ta có: f(m) ≥ 0 khi m ∈.
Vậy m ∈ thì phương trình đã cho có nghiệm.
Lời giải
Ta có hình vẽ mô phỏng quỹ đạo chuyển động của quả bóng như hình vẽ:
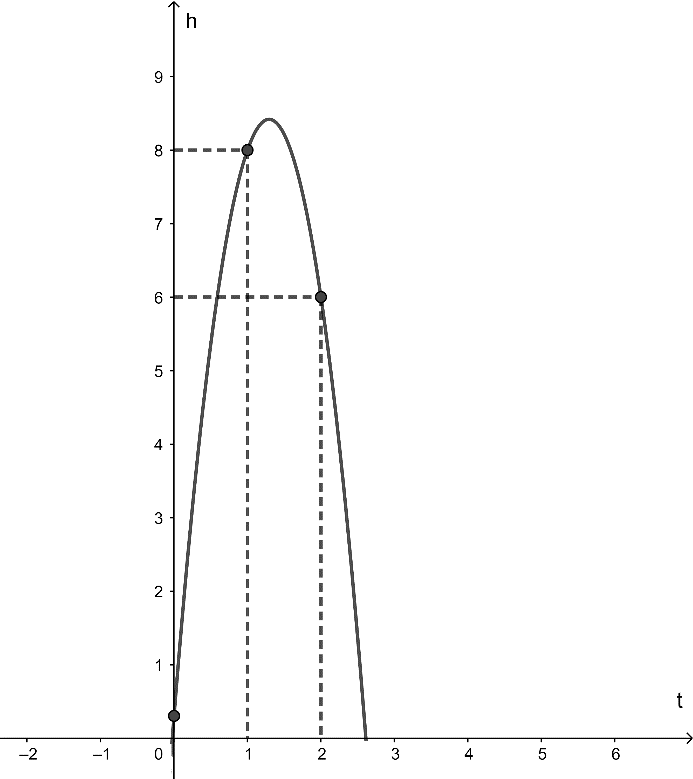
Vì quỹ đạo chuyển động là một đường thẳng parabol có dạng h = at2 + bt + c (a ≠ 0).
Một quả bóng được đá lên từ điểm A(0; 0,3) nên điểm A thuộc vào parabol, thay t = 0 và h = 0,3 vào đồ thị hàm số ta được: 0,3 = a.02 + b.0 + c ⇔ c = 0,3 (1).
Bóng đạt độ cao h = 8m sau t = 1 giây nên điểm có tọa độ (1; 8) thuộc vào parabol.
Thay t = 1 và h = 8 vào đồ thị hàm số ta được: 8 = a.12 + b.1 + c ⇔ a + b + c = 8 (2).
Bóng đạt độ cao h = 6m sau t = 2 giây nên điểm có tọa độ (2; 6) thuộc vào parabol.
Thay t = 2 và h = 6 vào đồ thị hàm số ta được: 6 = a.22 + b.2 + c ⇔ 4a + 2b + c = 6 (3).
Từ (1), (2) và (3) ta có hệ phương trình: .
Ta có phương trình parabol cần tìm là: h = – 4,85t2 + 12,55t + 0,3.
Để chiều cao lớn hơn 5 thì h > 5 ⇔ – 4,85t2 + 12,55t + 0,3 > 5
⇔ – 4,85t2 + 12,55t – 4,7 > 0
Xét tam thức bậc hai f(t) = – 4,85t2 + 12,55t – 4,7, có a = – 4,85, ∆ = 12,552 – 4.(– 4,85).(– 4,7) = 66,3225 > 0.
Suy ra tam thức có hai nghiệm phân biệt t1 ≈ 0,454 và t2 ≈ 2,133.
Áp dụng định lí về dấu của tam thức bậc hai ta được: f(t) > 0 hay – 4,85t2 + 12,55t – 4,7 > 0 khi t ∈ (0,454; 2,133).
Để chiều cao nhỏ hơn 7 thì h < 7 ⇔ – 4,85t2 + 12,55t + 0,3 < 7
⇔ – 4,85t2 + 12,55t – 6,7 < 0
Xét tam thức bậc hai g(t) = – 4,85t2 + 12,55t – 6,7, có a = – 4,85, ∆ = 12,552 – 4.(– 4,85).(– 6,7) = 27,5225 > 0.
Suy ra tam thức có hai nghiệm phân biệt t1 ≈ 0,753 và t2 ≈ 1,835.
Áp dụng định lí về dấu của tam thức bậc hai ta được: g(t) < 0 hay – 4,85t2 + 12,55t – 6,7 < 0 khi t ∈ (– ∞; 0,753) ∪ (1,835; +∞).
Để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì t phải thuộc vào giao của hai tập (0,454; 2,133) hoặc (– ∞; 0,753) ∪ (1,835; +∞).
Ta có (0,454; 2,133) (– ∞; 0,753) ∪ (1,835; +∞) = (0,454; 0,753) ∪ (1,835; 2,133).
Vậy để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì thuộc khoảng 0,454 giây đến 0,753 giây hoặc 1,835 giây đến 2,133 giây.
Lời giải
Viên đạn đang ở độ cao hơn 15m nghĩa là: > 15
Xét tam thức f(x) = , có a = và
∆ = > 0.
Do đó tam thức có hai nghiệm phân biệt x1 ≈ 2 720,76 và x2 ≈ 612,57.
Áp dụng định lí về dấu ta có: f(x) > 0 hay khi x ∈ (612,57; 2 720,76).
Vậy khi viên đạn đang ở độ cao hơn 15m thì có khoảng cách đến vị trí bắn trong khoảng 612,57 m đến 2 720,76 m.
Bài giảng Toán 10 Bài 4: Bất phương trình bậc hai một ẩn - Cánh diều
Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
Bài 3: Dấu của tam thức bậc hai
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°
Lý thuyết Bất phương trình bậc hai một ẩn
1. Bất phương trình bậc hai một ẩn
– Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng sau: ax2 + bx + c < 0; ax2 + bx + c ≤ 0; ax2 + bx + c > 0; ax2 + bx + c ≥ 0, trong đó a, b, c là các số thực đã cho, a ≠ 0.
– Đối với bất phương trình bậc hai có dạng ax2 + bx + c < 0, mỗi số x0 ∈ ℝ sao cho được gọi là một nghiệm của bất phương trình đó.
Tập hợp các nghiệm x như thế còn được gọi là tập nghiệm của bất phương trình bậc hai đã cho.
Nghiệm và tập nghiệm của các dạng bất phương trình bậc hai ẩn x còn lại được định nghĩa tương tự.
Ví dụ: Cho bất phương trình bậc hai một ẩn (1). Trong các giá trị sau đây của x, giá trị nào là nghiệm của bất phương trình (1)?
a) x = 2;
b) x = 0;
c) x = 3.
Hướng dẫn giải
a) Với x = 2, ta có: 22 – 3.2 + 2 = 0. Vậy x = 2 là nghiệm của bất phương trình (1).
b) Với x = 0, ta có: 02 – 3.0 + 2 = 2 > 0.Vậy x = 0 không phải là nghiệm của bất phương trình (1).
c) Với x = 3, ta có: 32 – 3.3 + 3 > 0. Vậy x = 3 không phải là nghiệm của bất phương trình (1).
Chú ý: Giải bất phương trình bậc hai ẩn x là đi tìm tập nghiệm của bất phương trình đó.
2. Giải bất phương trình bậc hai một ẩn
2.1. Giải bất phương trình bậc hai một ẩn bằng cách xét dấu của tam thức bậc hai
Nhận xét: Để giải bất phương trình bậc hai (một ẩn) có dạng:
f(x) > 0 (f(x) = ax2 + bx + c), ta chuyển việc giải bất phương trình đó về việc tìm tập hợp những giá trị của x sao cho f(x) mang dấu “+”. Cụ thể, ta làm như sau:
Bước 1. Xác định dấu của hệ số a và tìm nghiệm của f(x) (nếu có).
Bước 2. Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho f(x) mang dấu “+”.
Chú ý: Các bất phương trình bậc hai có dạng f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 được giải bằng cách tương tự.
Ví dụ: Giải các bất phương trình bậc hai sau:
a) ;
b) .
Hướng dẫn giải
a) Tam thức bậc hai có hai nghiệm phân biệt , và có hệ số a = 1 > 0. Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức mang dấu “+” là
Vậy tập nghiệm của bất phương trình là
b) Tam thức bậc hai có hai nghiệm , và có hệ số .
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức mang dấu “+” là (– 4; 1).
Vậy tập nghiệm của bất phương trình – x2 – 3x + 4 > 0 là (4; 1).
2.2. Giải bất phương trình bậc hai một ẩn bằng cách sử dụng đồ thị
– Giải bất phương trình bậc hai ax2 + bx + c > 0 là tìm tập hợp những giá trị của x ứng với phần parabol y = ax2 + bx + c nằm phía trên trục hoành.
– Tương tự, giải bất phương trình bậc hai ax2 + bx + c < 0 là tìm tập hợp những giá trị của x ứng với phần parabol y = ax2 + bx + c nằm phía dưới trục hoành.
Như vậy, để giải bất phương trình bậc hai (một ẩn) có dạng:
f(x) > 0 (f(x) = ax2 + bx + c) bằng cách sử dụng đồ thị, ta có thể làm như sau: Dựa vào parabol y = ax2 + bx + c, ta tìm tập hợp những giá trị của x ứng với phần parabol đó nằm phía trên trục hoành. Đối vổi các bất phương trình bậc hai có dạng f(x) < 0, f(x) ≥ 0, ,f(x) ≤ 0, ta cũng làm tương tự.
Ví dụ: Quan sát đồ thị và giải các bất phương trình bậc hai sau:
a)
b) > 0
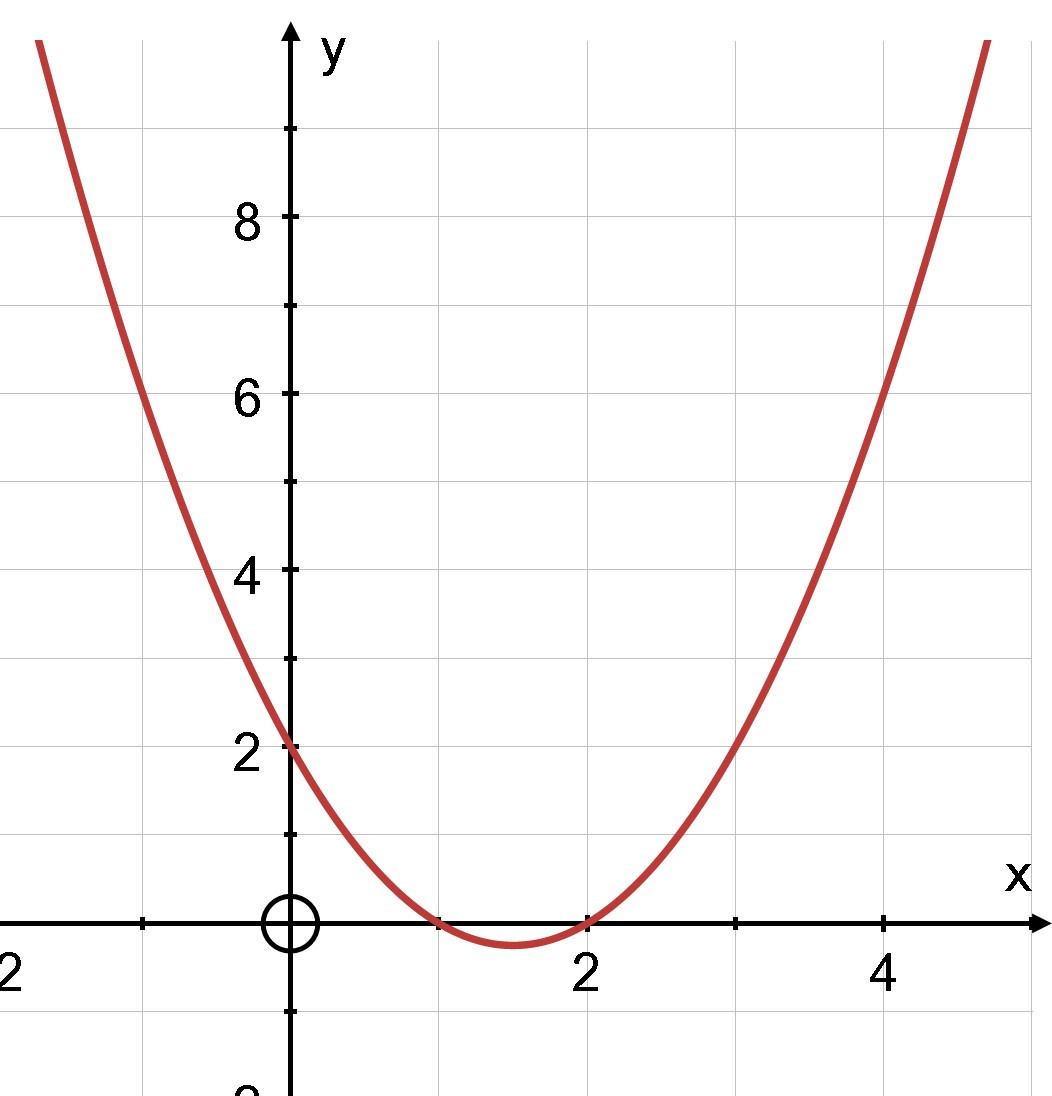
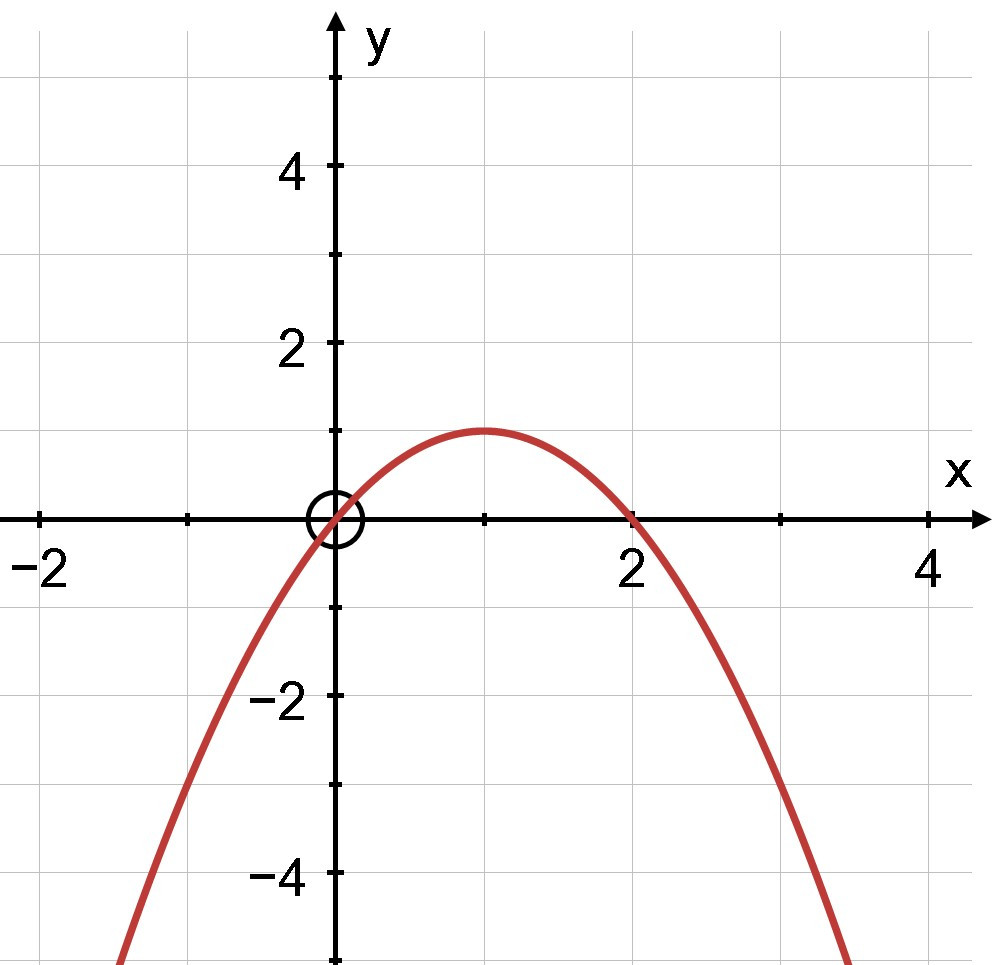
Đồ thị y = Đồ thị y =
Hướng dẫn giải
a) Quan sát đồ thị, ta thấy biểu diễn phần parabol y = nằm phía dưới trục hoành, tương ứng với 1 < x < 2.
Vậy tập nghiệm của bất phương trình là khoảng (1; 2).
b) Quan sát đồ thị, ta thấy > 0 biểu diễn phần parabol y = nằm phía trên trục hoành, tương ứng với 0 < x < 2.
Vậy tập nghiệm của bất phương trình > 0 là khoảng (0 ; 2).
2.3. Ứng dụng của bất phương trình bậc hai một ẩn
Bất phương trình bậc hai một ẩn có nhiều ứng dụng, chẳng hạn: giải một số hệ bất phương trình; ứng dụng vào tính toán lợi nhuận trong kinh doanh; tính toán điểm rơi trong pháo binh;...
Chúng ta sẽ làm quen với những ứng dụng đó qua một số ví dụ sau đây.
Ví dụ 4: Tìm giao các tập nghiệm của hai bất phương trình sau:
(3) và (4)
Hướng dẫn giải
Ta có: Tập nghiệm của bất phương trình (3) là S3= (−3 ; 1);
Tập nghiệm của bất phương trình (4) là S4= (1 ; 3).
Giao các tập nghiệm của hai bất phương trình trên là:
.