Với lời giải SBT Toán 11 trang 82 Tập 1 chi tiết trong Bài tập cuối chương 3 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài tập cuối chương 3
Bài 32 trang 82 SBT Toán 11 Tập 1: Cho limun = 2, limvn = 3. Khi đó, lim(un + vn) bằng:
A. 6.
B. 5.
C. 1
D. 2.
Lời giải:
Đáp án đúng là: B
Ta có lim(un + vn) = limun + limvn = 2 + 3 = 5.
Bài 33 trang 82 SBT Toán 11 Tập 1: Cho limun = 3, lim vn = +∞. Khi đó bằng:
A. 3.
B. –∞.
C. +∞.
D. 0.
Lời giải:
Đáp án đúng là: C
Vì limun = 3 > 0, lim vn = +∞ nên .
Bài 34 trang 82 SBT Toán 11 Tập 1: Cho hai dãy số (un), (vn) với , . Khi đó, bằng:
A. 3.
B. 4.
C. 5.
D. 2.
Lời giải:
Đáp án đúng là: A
Ta có ;
Và .
Suy ra .
Khi đó .
Bài 35 trang 82 SBT Toán 11 Tập 1: Biểu diễn dưới dạng phân số của 1,(7) là:
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Ta có: 1,(7) = 1 + 0,(7) = 1 + 0,7 + 0,07 + 0,007 + ... + 0,00007 + ...
Vì 0,7; 0,07; 0,007; ... lập thành một cấp số nhân lùi vô hạn với số hạng đầu u1 = 0,7 và công bội q = 0,1 < 1 nên
0,7 + 0,07 + 0,007 + ... + 0,00007 + ... = .
Vậy 1,(7) = 1 + .
Bài 36 trang 82 SBT Toán 11 Tập 1: Cho . Khi đó, bằng:
A. 5.
B. 2.
C. 10.
D. 7.
Lời giải:
Đáp án đúng là: C
Ta có .
Bài 37 trang 82 SBT Toán 11 Tập 1: Giả sử . Khi đó bằng:
A. 4.
B. 2.
C. 6.
D. Không tồn tại.
Lời giải:
Đáp án đúng là: D
Ta có nên .
Suy ra không tồn tại .
Bài 38 trang 82 SBT Toán 11 Tập 1: Nếu thì 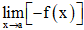
A. +∞.
B. –∞.
C. a.
D. – a.
Lời giải:
Đáp án đúng là: B
Ta có: 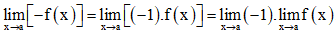
Mà và .
Do vậy, . Vậy 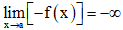
Bài 39 trang 82 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số trong Hình 9 và cho biết:
a) bằng:
A. 2.
B. 1.
C. +∞.
D. –∞.
b) bằng:
A. 2.
B. 1.
C. +∞.
D. –∞.
c) Hàm số y = f(x) liên tục trên khoảng:
A. (–∞; 1).
B. (–∞; +∞).
C. (1; +∞).
D. (–∞; 2).
Lời giải:
a) Đáp án đúng là: A
Quan sát đồ thị ta thấy khi x → +∞ thì f(x) → 2.
Vậy .
b) Đáp án đúng là: D
Quan sát đồ thị ta thấy .
c) Đáp án đúng là: C
Quan sát đồ thị ta thấy, hàm số y = f(x) liên tục trên khoảng (1; +∞).
Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 32 trang 82 SBT Toán 11 Tập 1: Cho limun = 2, limvn = 3. Khi đó, lim(un + vn) bằng:....
Bài 33 trang 82 SBT Toán 11 Tập 1: Cho limun = 3, lim vn = +∞. Khi đó bằng:...
Bài 34 trang 82 SBT Toán 11 Tập 1: Cho hai dãy số (un), (vn) với , . Khi đó, bằng:....
Bài 35 trang 82 SBT Toán 11 Tập 1: Biểu diễn dưới dạng phân số của 1,(7) là:....
Bài 36 trang 82 SBT Toán 11 Tập 1: Cho . Khi đó, bằng:....
Bài 37 trang 82 SBT Toán 11 Tập 1: Giả sử . Khi đó bằng:....
Bài 38 trang 82 SBT Toán 11 Tập 1: Nếu thì 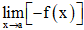
Bài 39 trang 82 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số trong Hình 9 và cho biết:.......
Bài 40 trang 83 SBT Toán 11 Tập 1: Hàm số nào sau đây không liên tục trên tập xác định của nó?.....
Bài 42 trang 83 SBT Toán 11 Tập 1: Tính các giới hạn sau:......
Bài 44 trang 83 SBT Toán 11 Tập 1: Tính các giới hạn sau:....
Bài 45 trang 83 SBT Toán 11 Tập 1: Cho hàm số 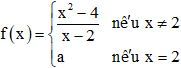
Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian