Cho tam giác T1 có diện tích bằng 1. Giả sử có tam giác T2 đồng dạng với tam giác T1

Cho tam giác T1 có diện tích bằng 1. Giả sử có tam giác T2 đồng dạng với tam giác T1

Van Anh Ngày: 18-08-2023 Lớp 11

1 K

Với giải Bài 43 trang 83 SBT Toán lớp 11 Cánh diều chi tiết trong Bài tập cuối chương 3 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11 . Mời các bạn đón xem:

Giải SBT Toán 11 Bài tập cuối chương 3

Bài 43 trang 83 SBT Toán 11 Tập 1: Cho tam giác T₁ có diện tích bằng 1. Giả sử có tam giác T₂ đồng dạng với tam giác T₁, tam giác T₃ đồng dạng với tam giác T₂, ..., tam giác T_n đồng dạng với tam giác T_{n – 1} với tỉ số đồng dạng $\frac{1}{k} (k > 1)$ . Khi n tiến tới vô cùng, tính tổng diện tích của tất cả các tam giác theo k.

Lời giải:

Gọi diện tích các tam giác T₁; T₂; ...; T_{n – 1}; T_n lần lượt là S₁; S₂; ...; S_{n – 1}; S_n.

Vì tam giác T_n đồng dạng với tam giác T_{n – 1} với tỉ số đồng dạng $\frac{1}{k}$ nên diện tích tam giác T_n bằng $\frac{1}{k^{2}}$ diện tích tam giác T_{n – 1} hay $S_{n} = \frac{1}{k^{2}} S_{n - 1}$ .

Vì k > 1 nên $\frac{1}{k^{2}} < 1$ . Vậy S₁; S₂; ...; S_{n – 1}; S_n; ... lập thành một cấp số nhân lùi vô hạn có số hạng đầu S₁ = 1 và công bội $q = \frac{1}{k^{2}}$ .

Khi đó, tổng diện tích của tất cả các tam giác nếu n tiến tới vô cùng là:

S = S₁ + S₂ + ... + S_{n – 1} + S_n + ... = $\frac{1}{1 - \frac{1}{k^{2}}} = \frac{k^{2}}{k^{2} - 1}$ .

Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 32 trang 82 SBT Toán 11 Tập 1: Cho limu_n = 2, limv_n = 3. Khi đó, lim(u_n + v_n) bằng:....

Bài 33 trang 82 SBT Toán 11 Tập 1: Cho limu_n = 3, lim v_n = +∞. Khi đó $\lim \frac{v_{n}}{u_{n}}$ bằng:...

Bài 34 trang 82 SBT Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với $u_{n} = 1 - \frac{2}{n}$ , $v_{n} = 4 + \frac{2}{n + 2}$ . Khi đó, $\lim (u_{n} + \sqrt{v_{n}})$ bằng:....

Bài 35 trang 82 SBT Toán 11 Tập 1: Biểu diễn dưới dạng phân số của 1,(7) là:....

Bài 36 trang 82 SBT Toán 11 Tập 1: Cho $\lim_{x \to 2} f (x) = 5$ . Khi đó, $\lim_{x \to 2} 2 f (x)$ bằng:....

Bài 37 trang 82 SBT Toán 11 Tập 1: Giả sử $\lim_{x \to 3^{+}} f (x) = 4, \lim_{x \to 3^{-}} f (x) = 2$ . Khi đó $\lim_{x \to 3} f (x)$ bằng:....

Bài 38 trang 82 SBT Toán 11 Tập 1: Nếu 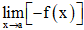$\lim_{x \to a} f (x) = + \infty$ thì bằng:....

Bài 39 trang 82 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số trong Hình 9 và cho biết:.......

Bài 40 trang 83 SBT Toán 11 Tập 1: Hàm số nào sau đây không liên tục trên tập xác định của nó?.....

Bài 41 trang 83 SBT Toán 11 Tập 1: Hàm số y = tan x gián đoạn tại bao nhiêu điểm trên khoảng (0; 2π)?.....

Bài 42 trang 83 SBT Toán 11 Tập 1: Tính các giới hạn sau:......

Bài 43 trang 83 SBT Toán 11 Tập 1: Cho tam giác T₁ có diện tích bằng 1. Giả sử có tam giác T₂ đồng dạng với tam giác T₁, tam giác T₃ đồng dạng với tam giác T₂, ..., tam giác T_n đồng dạng với tam giác T_{n – 1} với tỉ số đồng dạng $\frac{1}{k} (k > 1)$ . Khi n tiến tới vô cùng, tính tổng diện tích của tất cả các tam giác theo kk......

Bài 44 trang 83 SBT Toán 11 Tập 1: Tính các giới hạn sau:....

Bài 45 trang 83 SBT Toán 11 Tập 1: Cho hàm số 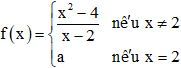Cho hàm số trang 83 SBT Toán 11 . Tìm a để hàm số liên tục trên ℝ. ....

Bài 46 trang 84 SBT Toán 11 Tập 1: Một bể chứa 5 000 l nước tinh khiết. Nước muối có chứa 30 gam muối trên mỗi lít nước được bơm vào bể với tốc độ 25 l/phút.....

Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

137

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.