Với lời giải SBT Toán 10 trang 42 Tập 1 chi tiết trong Bài 1: Hàm số và đồ thị sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 1: Hàm số và đồ thị

Bài 1 trang 42 SBT Toán 10 Tập 1: Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?

A. x + 2y = 3.

B. y = $\sqrt{x^2-2x}$.

C. y = $\frac{1}{x}$.

D. x² + y² = 4.

Lời giải

Đáp án đúng là D

Xét công thức x + 2y = 3 ⇔ y = $\frac{-1}{2}$x + 3;

Với mỗi giá trị của x ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.

Xét công thức y = $\sqrt{x^2-2x}$

Với mỗi giá trị của x ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.

Xét công thức y = $\frac{1}{x}$

Với mỗi giá trị x ≠ 0 ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.

Xét công thức: x² + y² = 4 ⇔ y² =  – x² + 4 ⇔ y = $\pm \sqrt{-x^2+4}$.

Ta thấy ở công thức này, với mỗi giá trị của x thỏa mãn điều kiện – x² + 4 ≥ 0 ta xác định được 2 giá trị của y. Do đó công thức này không biểu diễn y là hàm số của x.

Bài 2 trang 42 SBT Toán 10 Tập 1: Cho đồ thị hàm số y = f(x) ở Hình 4. Phát biểu nào sau đây là đúng?

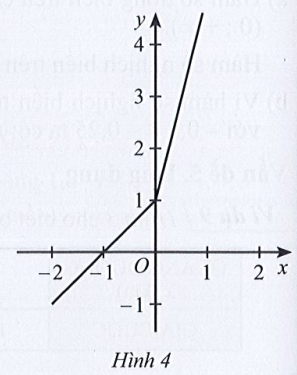
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.

B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 1.

C. Hàm số đồng biến trên khoảng (– 1; +∞), nghịch biến trên khoảng ( – ∞; – 1).

D. Hàm số đồng biến trên ℝ.

Lời giải

Đáp án đúng là D

Quan sát đồ thị ta thấy:

Hàm số xác định trên ℝ, và trên ℝ hàm số đi lên nên hàm đồng biến trên ℝ. Do đó C sai và D đúng.

Đồ thị hàm số cắt Ox tại điểm có hoành độ bằng – 1. Do đó A sai.

Đồ thị hàm số cắt Oy tại điểm có tung độ bằng 1. Do đó B sai.

Bài 3 trang 42 SBT Toán 10 Tập 1: Tìm tập xác định của mỗi hàm số sau:

a) y = – x³ + 4x – 1;

b) y = $\sqrt{5-6x}$;

c) y = $\frac{4}{3x+1}$;

d) y = $\frac{1}{2x-1}-\sqrt{3-x}$;

e) y = $\frac{2x+3}{x^2+3x-4}$;

f) y = $\left\{\begin{array}{l}x-1khix>0\\ 5x+1khix<-1\end{array}\right.$.

Lời giải

a) Biểu thức – x³ + 4x – 1 xác định với mọi giá trị của x ∈ ℝ.

Do đó tập xác định của hàm số  y = – x³ + 4x – 1 là D = ℝ.

Vậy D = ℝ.

b) Biểu thức $\sqrt{5-6x}$ xác định khi 5 – 6x ≥ 0 ⇔ x ≤ $\frac{5}{6}$.

Do đó tập xác định của hàm số y = $\sqrt{5-6x}$ là D = $\left(-\infty ;\frac{5}{6}\right]$.

Vậy D = $\left(-\infty ;\frac{5}{6}\right]$.

c) Biểu thức $\frac{4}{3x+1}$ xác định khi 3x + 1 ≠ 0 ⇔ x ≠ $-\frac{1}{3}$.

Do đó tập xác định của hàm số y = $\frac{4}{3x+1}$ là D = ℝ \ $\left\{-\frac{1}{3}\right\}$.

Vậy D = ℝ \ $\left\{-\frac{1}{3}\right\}$.

d) Biểu thức $\frac{1}{2x-1}$ xác định khi 2x – 1 ≠ 0 ⇔ x ≠ $\frac{1}{2}$ và biểu thức $\sqrt{3-x}$ xác định khi 3 – x  ≥  0 ⇔ x ≤ 3.

Do đó tập xác định của hàm số y = $\frac{1}{2x-1}-\sqrt{3-x}$ là D = ( –∞; 3) \ $\left\{\frac{1}{2}\right\}$.

Vậy D =  ( –∞; 3) \ $\left\{\frac{1}{2}\right\}$.

e) Biểu thức $\frac{2x+3}{x^2+3x-4}$ xác định khi x² + 3x – 4 ≠ 0 ⇔ x ≠ 1 và x ≠ – 4.

Do đó tập xác định của hàm số y = $\frac{2x+3}{x^2+3x-4}$ là D = ℝ \{1; – 4}.

Vậy D = ℝ \{1; – 4}.

f) Biểu thức x – 1 luôn xác định với x > 0 và biểu thức 5x + 1 luôn xác định với x < – 1. Do đó tập xác định của hàm số y = $\left\{\begin{array}{l}x-1khix>0\\ 5x+1khix<-1\end{array}\right.$ là D = (– ∞; – 1) ∪ (0; + ∞).

Vậy D = (– ∞; – 1) ∪ (0; + ∞).

Bài 4 trang 42 SBT Toán 10 Tập 1: Cho hàm số: f(x) = $\left\{\begin{array}{l}-x+1khix<0\\ 0khix=0\\ 1khix>0\end{array}\right.$.

a) Tìm tập xác định của hàm số trên.

b) Tính giá trị của hàm số khi x = – 2; x = 0; x = 2 021.

Lời giải

a) Biểu thức – x + 1 luôn xác định với x < 0, biểu thức 0 luôn xác định với x = 0 và biểu thức 1 luôn xác định với x > 0.

Do đó tập xác định của hàm số f(x) là D = ℝ.

Vậy D = ℝ.

b) Với x = – 2 < 0 thì f(x) = – x + 1. Khi đó thay x = 2 vào hàm số ta được: f(– 2) = – (– 2) + 1 = 3.

Với x = 0 thì f(x) = 0. Khi đó thay x = 0 vào hàm số ta được: f(0) = 0.

Với x = 2 021 > 1 thì f(x) = 1. Khi đó thay x = 2 021 vào hàm số ta được: f(2 021) = 1.

Vậy giá trị của hàm số tại x = – 2; x = 0; x = 2 021 lần lượt là f(– 2) = 3; f(0) = 0 và f(2 021) = 1.

Xem thêm các bài giải sách bài tập Toán 10 Cánh diều hay, chi tiết khác:

Giải SBT Toán 10 trang 43 Tập 1

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài ôn tập chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc nhất một ẩn