Với lời giải SBT Toán 11 trang 76 Tập 1 chi tiết trong Bài 1: Giới hạn của dãy số sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 1: Giới hạn của dãy số

Bài 4 trang 76 SBT Toán 11 Tập 1: Cho hai dãy số (u_n) và (v_n) có limu_n = 3, limv_n = 4. Tìm các giới hạn sau:

a) lim(3u_n ‒ 4); b) lim(u_n + 2v_n);

c) lim(u_n ‒ v_n)²; d) $\text{lim}\frac{-2u_n}{v_n-2u_n}$

Lời giải:

a) lim(3u_n ‒ 4) = 3limu_n ‒ lim4 = 3.3 ‒ 4 = 5.

b) lim(u_n + 2v_n) = limu_n + 2limv_n = 3 + 2.4 = 11.

c) lim(u_n ‒ v_n)² = (limu_n ‒ limv_n)² = (3 ‒ 4)² = 1.

d) $\text{lim}\frac{-2u_n}{v_n-2u_n}=\frac{-2\lim u_n}{\lim v_n-2\lim u_n}=\frac{-2\cdot 3}{4-2\cdot 3}=3.$

Bài 5 trang 76 SBT Toán 11 Tập 1: Cho dãy số (u_n) thoả mãn limnu_n = 3. Tìm giới hạn $\text{lim}\frac{2n+3}{n^2{u}_n}$.

Lời giải:

Ta có:

$\text{lim}\frac{2n+3}{n^2{u}_n}=\text{ lim}\left(\frac{2n+3}{n}\cdot \frac{1}{n{u}_n}\right)=\text{lim}\frac{2n+3}{n}\cdot \text{lim}\frac{1}{n{u}_n}$

$=\text{lim}\left(2+\frac{3}{n}\right)\cdot \frac{1}{\text{lim}n{u}_n}=2\cdot \frac{1}{3}=\frac{2}{3}.$

Bài 6 trang 76 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) lim(1 + 3n – n²);

b) $\text{lim}\frac{n^3+3n}{2n-1};$

c) $\text{lim}\left(\sqrt{n^2-n}+n\right);$

d) lim(3ⁿ⁺¹ – 5ⁿ).

Lời giải:

a) $1+3n-n^2=n^2\left(\frac{1}{n^2}+\frac{3}{n}-1\right)$

Ta có limn² = +∞ và $\lim \left(\frac{1}{n^2}+\frac{3}{n}-1\right)=0+0-1=-1.$

Suy ra $lim\left(1+3n–n^2\right)=\lim \left[n^2\left(\frac{1}{n^2}+\frac{3}{n}-1\right)\right]=-\infty .$

b) $\frac{n^3+3n}{2n-1}=\frac{n^3\left(1+\frac{3}{n^2}\right)}{n\left(2-\frac{1}{n}\right)}=n^2\cdot \frac{1+\frac{3}{n^2}}{2-\frac{1}{n}}$

Ta có limn² = +∞ và $\lim \frac{1+\frac{3}{n^2}}{2-\frac{1}{n}}=\frac{1}{2}.$

Suy ra $\text{lim}\frac{n^3+3n}{2n-1}=\text{lim}\left[n^2\cdot \frac{1+\frac{3}{n^2}}{2-\frac{1}{n}}\right]=+\infty .$

c) $\sqrt{n^2-n}+n=n\left(\sqrt{1-\frac{1}{n}}+1\right)$

Ta có limn = +∞ và $\lim \left(\sqrt{1-\frac{1}{n}}+1\right)=2.$

Suy ra $\text{lim}\left(\sqrt{n^2-n}+n\right)=\text{lim}\left[n\left(\sqrt{1-\frac{1}{n}}+1\right)\right]=+\infty .$

d) $3^{n+1}-5^n=5^n\left(\frac{3^{n+1}}{5^n}-1\right)=5^n\left[3\cdot {\left(\frac{3}{5}\right)}^n-1\right]$

Ta có lim5ⁿ = +∞ và $\lim \left[3\cdot {\left(\frac{3}{5}\right)}^n-1\right]=-1$

Suy ra $\text{lim}\left(3^{n+1}-5^n\right)=\text{lim}\left\{5^n\cdot \left[3\cdot {\left(\frac{3}{5}\right)}^n-1\right]\right\}=-\infty .$

Bài 7 trang 76 SBT Toán 11 Tập 1: Tuỳ theo giá trị của a > 0, tìm giới hạn $\text{lim}\frac{a^n}{a^n+1}$.

Lời giải:

⦁ Nếu 0 < a < 1 thì limaⁿ = 0 nên $\text{lim}\frac{a^n}{a^n+1}=\frac{\text{lim}{a}^n}{\text{lim}{a}^n+1}=\frac{0}{0+1}=0.$

⦁ Nếu a = 1 thì $\text{lim}\frac{a^n}{a^n+1}=\text{lim}\frac{1^n}{1^n+1}=\text{lim}\frac{1}{1+1}=\text{lim}\frac{1}{2}=\frac{1}{2}.$

⦁ Nếu a > 1, ta viết $\frac{a^n}{a^n+1}=\frac{1}{1+{\left(\frac{1}{a}\right)}^n}$(chia cả tử và mẫu cho aⁿ)

Do a > 1 nên $0<\frac{1}{a}<1$, suy ra $\text{lim}{\left(\frac{1}{a}\right)}^n=0$. Từ đó,

$\text{lim}\frac{a^n}{a^n+1}=\text{lim}\frac{1}{1+{\left(\frac{1}{a}\right)}^n}=\frac{1}{1+\text{lim}{\left(\frac{1}{a}\right)}^n}=\frac{1}{1+0}=1.$

Vậy $\text{lim}\frac{a^n}{a^n+1}$ bằng 0 nếu 0 < a < 1; bằng $\frac{1}{2}$ nếu a = 1; bằng 1 nếu a > 1.

Bài 8 trang 76 SBT Toán 11 Tập 1: Tính tổng của các cấp số nhân lùi vô hạn:

a) $1-\frac{1}{5}+\frac{1}{5^2}-\frac{1}{5^3}+\dots +{\left(-\frac{1}{5}\right)}^n+\dots$

b) $2+\frac{2^2}{3}+\frac{2^3}{3^2}+\dots +\frac{2^n}{3^{n-1}}+\dots$

Lời giải:

a) Cấp số nhân lùi vô hạn có công bội $q=\frac{-\frac{1}{5}}{1}=-\frac{1}{5}$ thỏa mãn |q| < 1.

Vậy tổng của cấp số nhân là: $S=\frac{u_1}{1-q}=\frac{1}{1-\left(-\frac{1}{5}\right)}=\frac{5}{6}.$

b) Cấp số nhân lùi vô hạn có công bội $q=\frac{\frac{2^2}{3}}{2}=\frac{2}{3}$ thỏa mãn |q| < 1.

Vậy tổng của cấp số nhân là: $S=\frac{u_1}{1-q}=\frac{2}{1-\frac{2}{3}}=6.$

Bài 9 trang 76 SBT Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau thành phân số:

a) 0,(7) = 0,777...; b) 1,(45) = 1,454545...

Lời giải:

a) 0,(7) = 0,777...

= 0,7 + 0,07 + 0,007 + 0,0007 + 0,00007...

$=\mathrm{0,7}+\mathrm{0,7}\cdot \frac{1}{10}+\mathrm{0,7}\cdot \frac{1}{{10}^2}+\mathrm{0,7}\cdot \frac{1}{{10}^3}\mathrm{...}$

Đây là tổng cấp số nhân lùi vô hạn với số hạng đầu u₁ = 0,7 và công bội $q=\frac{1}{10}$ thõa mãn |q| < 1.

Tổng này bằng $\frac{\mathrm{0,7}}{1-\frac{1}{10}}=\frac{\mathrm{0,7}}{\mathrm{0,9}}=\frac{7}{9}.$

Vậy $\mathrm{0,}\left(7\right)=\mathrm{0,777...}=\frac{7}{9}.$

b) 1,(45) = 1,454545... = 1 + 0,454545…

Ta có 0,454545... = 0,45 + 0,0045 + 0,000045 + …

$=\mathrm{0,45}+\mathrm{0,45}\cdot \frac{1}{100}+\mathrm{0,45}\cdot \frac{1}{{100}^2}+\mathrm{...}$

Đây là tổng cấp số nhân lùi vô hạn với số hạng đầu u₁ = 0,45 và công bội $q=\frac{1}{100}$ thõa mãn |q| < 1.

Tổng này bằng $\frac{\mathrm{0,45}}{1-\frac{1}{100}}=\frac{\mathrm{0,45}}{\mathrm{0,99}}=\frac{45}{99}=\frac{5}{11}.$

Vậy $\mathrm{1,}\left(45\right)=\mathrm{1,454545...}=1+\frac{5}{11}=\frac{16}{11}.$

Bài 10 trang 76 SBT Toán 11 Tập 1: Tại một nhà máy, người ta đo được rằng 80% lượng nước sau khi sử dụng được xử lí và tái sử dụng. Với 100 m³ ban đầu được sử dụng lần đầu tại nhà máy, khi quá trình xử lí và tái sử dụng lặp lại mãi mãi, nhà máy sử dụng được tổng lượng nước là bao nhiêu?

Lời giải:

Lượng nước ban đầu là u₁ = 100

Lượng nước sau khi xử lý và tái sử dụng lần 1 là: 100.80% = 100.0,8

Lượng nước sau khi xử lý và tái sử dụng lần 2 là: 100.80%.80% = 100.(0,8)²

Lượng nước sau khi xử lý và tái sử dụng lần 3 là: 100.80%.80%.80% = 100.(0,8)³

....

Vậy tổng lượng nước sau khi xử lý và tái sử dụng mãi mãi là cấp số nhân lùi vô hạn với số hạng đầu là u₁ = 100 và công bội q = 0,8 thỏa mãn |q| < 1.

Tổng này bằng:

$$\begin{gathered} 100+100\cdot 0,8+100\cdot {\left(0,8\right)}^2+100\cdot {\left(0,8\right)}^3+\dots \\ =\frac{100}{1-0,8}=\frac{100}{0,2} \end{gathered}$$

$=500\left({\text{m}}^3\right).$

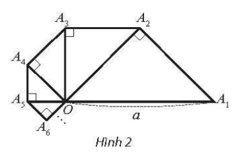
Bài 11 trang 76 SBT Toán 11 Tập 1: Cho tam giác OA₁A₂ vuông cân tại A₂ có cạnh huyền OA₁ bằng a. Bên ngoài tam giác OA₁A₂, vẽ tam giác OA₂A₃ vuông cân tại A₃. Tiếp theo, bên ngoài tam giác OA₂A₃, vẽ tam giác OA₃A₄ vuông cân tại A₄. Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc A₁A₂A₃A₄...

Lời giải:

Ta có các góc $\widehat{A_{1}O{A}_2},\widehat{A_{2}O{A}_3},\widehat{A_{3}O{A}_4},\dots$ đều bằng 45°. Ta có:

$A_1{A}_2=O{A}_2=O{A}_1\cdot \text{cos}{45}^{\circ }=a\frac{\sqrt{2}}{2};$

$$\begin{gathered} A_2{A}_3=O{A}_3=O{A}_2\cdot \text{cos}{45}^{\circ } \\ =a\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{2}}{2}=a{\left(\frac{\sqrt{2}}{2}\right)}^2 \end{gathered}$$

$$\begin{gathered} A_3{A}_4=O{A}_4=O{A}_3\cdot \text{cos}{45}^{\circ } \\ =a{\left(\frac{\sqrt{2}}{2}\right)}^2\cdot \frac{\sqrt{2}}{2}=a{\left(\frac{\sqrt{2}}{2}\right)}^3 \end{gathered}$$

Vậy độ dài các đoạn thẳng A₁A₂, A₂A₃, A₃A₄, ... tạo thành cấp số nhân lùi vô hạn với số hạng đầu $u_1=\frac{a\sqrt{2}}{2}$ và công bội $q=\frac{\sqrt{2}}{2}$ thỏa mãn |q| < 1.

Do đó, độ dài đường gấp khúc A₁A₂A₃A₄... là

$$\begin{gathered} l=\frac{a\sqrt{2}}{2}\cdot \frac{1}{1-\frac{\sqrt{2}}{2}}=\frac{a\sqrt{2}}{2-\sqrt{2}} \\ =\frac{a\sqrt{2}}{2}\cdot \left(2+\sqrt{2}\right)=a\left(1+\sqrt{2}\right). \end{gathered}$$