Với lời giải SBT Toán 11 trang 39 Tập 1 chi tiết trong Bài 7: Cấp số nhân sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 7: Cấp số nhân

Bài 2.21 trang 39 SBT Toán 11 Tập 1: Chứng minh rằng mỗi dãy số (u_n) sau là một cấp số nhân. Hãy tìm số hạng đầu và công bội của nó.

a) $u_n=-3.{\left(\frac{1}{2}\right)}^n$;

b) $u_n=\frac{2^n}{3^{n-1}}$.

Lời giải:

a) Từ $u_n=-3.{\left(\frac{1}{2}\right)}^n$ suy ra $u_{n+1}=-3.{\left(\frac{1}{2}\right)}^{n+1}=-\frac{3}{2}.{\left(\frac{1}{2}\right)}^n$.

Như vậy $\frac{u_{n+1}}{u_n}=\frac{-\frac{3}{2}.{\left(\frac{1}{2}\right)}^n}{-3.{\left(\frac{1}{2}\right)}^n}=\frac{1}{2}$ không đổi với mọi n.

Vậy dãy số đã cho là cấp số nhân có số hạng đầu u₁ = $-\frac{3}{2}$ và công bội $q=\frac{1}{2}$.

b) Từ $u_n=\frac{2^n}{3^{n-1}}$ suy ra $u_{n+1}=\frac{2^{n+1}}{3^{n+1-1}}=\frac{{2.2}^n}{{3.3}^{n-1}}=\frac{2}{3}.\frac{2^n}{3^{n-1}}$.

Như vậy $\frac{u_{n+1}}{u_n}=\frac{\frac{2}{3}.\frac{2^n}{3^{n-1}}}{\frac{2^n}{3^{n-1}}}=\frac{2}{3}$ không đổi với mọi n.

Vậy dãy số đã cho là cấp số nhân có số hạng đầu u₁ = 2 và công bội q = $\frac{2}{3}$.

Bài 2.22 trang 39 SBT Toán 11 Tập 1: Tìm số hạng thứ 10 của cấp số nhân 64, – 32, 16, – 8, ...

Lời giải:

Do cấp số nhân có u₁ = 64 và công bội q = $\frac{-32}{64}=-\frac{1}{2}$ nên số hạng thứ 10 của cấp số nhân là $u_{10}=u_1.q^{10-1}=u_1{q}^9=64.{\left(-\frac{1}{2}\right)}^9=-\frac{1}{8}$.

Bài 2.23 trang 39 SBT Toán 11 Tập 1: Cho một cấp số nhân với tất cả các các số hạng đều dương. Số hạng thứ 4 của cấp số nhân là 125 và số hạng thứ 10 là $\frac{125}{64}$. Tìm số hạng thứ 14 của cấp số nhân này.

Lời giải:

Theo giả thiết ta có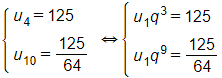 

Chia vế theo vế của hai phương trình trên ta được $q^6=\frac{1}{64}\iff q=\pm \frac{1}{2}$.

Với $q=\frac{1}{2}\Rightarrow u_1=\frac{125}{q^3}=\frac{125}{{\left(\frac{1}{2}\right)}^3}=1000\Rightarrow u_{14}=u_1{q}^{13}=1000.{\left(\frac{1}{2}\right)}^{13}=\frac{125}{1024}$.

Với $q=-\frac{1}{2}\Rightarrow u_1=\frac{125}{q^3}=\frac{125}{{\left(-\frac{1}{2}\right)}^3}=-1000$ < 0 (loại vì các số hạng của cấp số nhân đều là số dương).

Vậy số hạng thứ 14 của cấp số nhân đã cho là $u_{14}=\frac{125}{1024}$.

Bài 2.24 trang 39 SBT Toán 11 Tập 1: Tìm x sao cho x, x + 2, x + 3 là ba số hạng liên tiếp của một cấp số nhân.

Lời giải:

Vì x, x + 2 và x + 3 là ba số hạng liên tiếp của một cấp số nhân nên ta suy ra

x(x + 3) = (x + 2)²

⇔ x² + 3x = x² + 4x + 4

⇔ x = – 4.

Thử lại, ta có ba số là – 4; – 2; – 1 thoả mãn bài toán.

Vậy x = − 4.

Bài 2.25 trang 39 SBT Toán 11 Tập 1: Tính các tổng sau:

a) 1 + 4 + 16 + 64 + ... + 4⁹;

b) $\frac{1}{3}+\frac{2}{3}+\frac{2^2}{3}+\mathrm{...}+\frac{2^{12}}{3}$.

Lời giải:

a) Ta có 1 + 4 + 16 + 64 + ... + 4⁹ = 4⁰ + 4¹ + 4² + 4³ + ... + 4⁹.

Ta nhận thấy các số hạng của tổng trên là cấp số nhân có số hạng đầu u₁ = 4⁰ = 1, công bội q = 4 và có 10 số hạng.

Vậy 1 + 4 + 16 + 64 + ... + 4⁹ = $\frac{1.\left(1-4^{10}\right)}{1-4}$ = 349 525.

b) Ta có $\frac{1}{3}+\frac{2}{3}+\frac{2^2}{3}+\mathrm{...}+\frac{2^{12}}{3}$.

Ta nhận thấy các số hạng của tổng trên là cấp số nhân có số hạng đầu u₁ = $\frac{1}{3}$ và công bội q = 2 và có 13 số hạng.

Vậy $\frac{1}{3}+\frac{2}{3}+\frac{2^2}{3}+\mathrm{...}+\frac{2^{12}}{3}$$=\frac{\frac{1}{3}\left(1-2^{13}\right)}{1-2}=\frac{8191}{3}$.

Bài 2.26 trang 39 SBT Toán 11 Tập 1: Các bệnh truyền nhiễm có thể lây lan rất nhanh. Giả sử có năm người bị bệnh trong tuần đầu tiên của một đợt dịch, và mỗi người bị bệnh sẽ lây bệnh cho bốn người vào cuối tuần tiếp theo. Tính đến hết tuần thứ 10 của đợt dịch, có bao nhiêu người đã bị lây bởi căn bệnh này?

Lời giải:

Gọi u_n là số người bị bệnh ở cuối tuần thứ n. Vì có năm người bị bệnh trong tuần đầu tiên của một đợt dịch, và mỗi người bị bệnh sẽ lây bệnh cho bốn người vào cuối tuần tiếp theo nên dãy số (u_n) là một cấp số nhân có số hạng đầu u₁ = 5 và công bội q = 4.

Suy ra số người bị ảnh hưởng bởi dịch bệnh ở cuối tuần 10 là

u₁₀ = u₁q⁹ = 5 . 4⁹ = 1 310 720 (người).