Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Cấp số nhân, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Cấp số nhân. Mời các bạn đón xem:

Bài tập Toán 11 Cấp số nhân

A. Bài tập Cấp số nhân

Bài 1: Xác định công bội, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số nhân sau:

a) 1, 3, 9, ...;

b) 3, $\frac{-1}{3},\frac{1}{27}$, ….

Hướng dẫn giải

a) Ta thấy: 3 : 1 = 3, 9 : 3 = 3

Suy ra công bội q = 3

Số hạng tổng quát của cấp số nhân là: u_n = 3^n–1.

Số hạng thứ 5: u₅ = 3^5–1 = 81.

Số hạng thứ 100: u₁₀₀ = 3^100–1 = 3⁹⁹.

b) Ta thấy:

Suy ra cấp số nhân có công bội q = $\frac{-1}{9}$.

Số hạng tổng quát của cấp số nhân là: u_n = 3..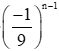

Số hạng thứ 5: u₅ = 3.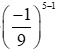= $\frac{1}{2187}$.

Số hạng thứ 100: u₁₀₀ =3.

Bài 2: Viết năm số hạng đầu của dãy số (u_n) sau và xem nó có phải là cấp số nhân không. Nếu nó là cấp số nhân, hãy tìm công bội q và viết công thức số hạng tổng quát của nó dưới dạng u_n = u₁ . q^n–1.

a) u_n = 4n;

b) u_n = 3ⁿ;

c) u₁ = 2, u_n = nu_n–1.

Hướng dẫn giải

a) Năm số hạng đầu của dãy là: 4, 8, 12, 16, 20

Ta có: 8 : 4 = 2 ≠ 12 : 8 = $\frac{3}{2}$ nên (u_n) không phải là cấp số nhân.

b) Năm số hạng đầu của dãy là: 3; 9; 27; 81; 243

Ta có: $\frac{u_n}{u_{n-1}}=\frac{3^n}{3^{n-1}}=3$ với mọi n ≥ 2

Suy ra dãy số là cấp số nhân với u₁ = 3 và công bội q = 3.

Số hạng tổng quát: u_n = 3 . 3^n–1.

c) Năm số hạng đầu của dãy là: 2; 4; 12; 48; 240

Ta có: 4 : 2 = 2 ≠ 12 : 4 = 3 nên (u_n) không phải là cấp số nhân.

Bài 3: Một cấp số nhân có số hạng thứ 6 bằng 10 240 và số hạng thứ 3 bằng 160. Tìm số hạng thứ 50 của cấp số nhân này.

Hướng dẫn giải

Giả sử u₁ là số hạng đầu và q là công bội của cấp số nhân đó. Ta có:

u₆ = u₁ . q⁵ = 10 240 (1)

u₃ = u₁ . q² = 160 (2)

Lấy (1) chia vế theo vế (2) ta được: q³ = 64. Suy ra q = 4.

Với q = 4, ta tính được u^­₁ = 10.

Suy ra công thức số hạng tổng quát của cấp số nhân là: u_n = 10 . 4^n–1

Vậy số hạng thứ 50 của cấp số nhân này là u₅₀ = 10 . 4^50–1 = 10 . 4⁴⁹.

Bài 4: Một cấp số nhân có số hạng đầu bằng 4 và công bội bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số nhân này để có tổng bằng 131 068?

Hướng dẫn giải

Số hạng tổng quát của cấp số nhân là: u_n = 4 . 2^n–1.

Gọi n là số các số hạng cần lấy tổng, ta có

131 068 = S_n = 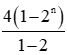 = 4 . 2ⁿ – 4

Suy ra: 2ⁿ = 32768 = 2¹⁵, do đó n = 15.

Vậy ta phải lấy 15 số hạng đầu của cấp số nhân.

Bài 5. Cho cấp số nhân (u_n) có u₂ = 2 và u₅ = 16. Tìm q và u₁ của cấp số nhân đã cho.

Hướng dẫn giải

Ta có:

• u₂ = u₁.q ⇔ 2 = u₁.q

• u₅ = u₁.q⁴ ⇔ 16 = u₁.q⁴

Khi đó $\frac{u_5}{u_2}=\frac{u_1.q^4}{u_1.q}=q^3$ ⇔ q³ = 8 ⇔ q = 2.

Do đó u₁ = 1.

Vậy q = 2 và u₁ = 1.

Bài 6. Dãy số (u_n) có u_n = 4.3n có phải là cấp số nhân không? Nếu phải hãy xác định công bội?

A. q = 3;

B. q = 2;

C. q = 4;

D. q = 1.

Hướng dẫn giải

Đáp án đúng là: A

Ta có: $\frac{u_{n+1}}{u_n}=\frac{{4.3}^{n+1}}{{4.3}^n}=3$ không phụ thuộc vào n.

Vậy dãy số (u_n) là một cấp số nhân với công bội q = 3.

Bài 7. Cho cấp số nhân (u_n) có u₁ = 3 và $q=\frac{1}{2}.$ Tính tổng 8 số hạng đầu tiên của cấp số nhân đã cho.

A. $\frac{765}{256};$

B. $\frac{765}{128};$

C. $\frac{265}{756};$

D. $\frac{128}{265}.$

Hướng dẫn giải

Đáp án đúng là: B

Bài 8. Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a) –2, 4, –8, 16, –32, 64, –128, 256.

b) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Hướng dẫn giải

a) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp –2 lần số hạng trước của dãy.

Vì vậy dãy –2, 4, –8, 16, –32, 64, –128, 256 là cấp số nhân với số hạng đầu u₁ = –2 và công bội q = –2.

b) Ta có $\frac{4}{1}\ne \frac{9}{4}$ nên dãy 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 không phải là cấp số nhân.

Bài 9. Cho dãy số (u_n) có u_n = (–1)ⁿ⁺¹ . 3²ⁿ⁺¹. Chứng minh dãy (u_n) là một cấp số nhân. Chỉ rõ u₁ và công bội q.

Hướng dẫn giải

Ta xét tỉ số:

.

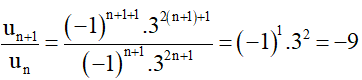
Suy ra dãy số (u_n) là một cấp số nhân có công bội q = –9 và u₁ = (–1)¹⁺¹ . 3^2.1+1 = 27.

Vậy u₁ = 27 và q = –9.

Bài 10. Cho cấp số nhân (u_n) có u₅ = 8 và u₁₁ = 512.

a) Tính số hạng đầu u₁ và công bội q của cấp số nhân (biết công bội q > 0).

b) Tính u₂₀ và S₂₀.

Hướng dẫn giải

a) Ta có 

Do q > 0 nên $\frac{u_{11}}{u_5}=\frac{u_1.q^{10}}{u_1.q^4}=q^6=64\Rightarrow q=2$ (do q > 0).

Thay q = 2 trở lại hệ ta được u₁ = $\frac{1}{2}$.

Vậy cấp số nhân đã cho có u₁ = $\frac{1}{2}$ và q = 2.

b) Ta có u₂₀ = u₁.q^{20 – 1} = u₁.q¹⁹ = $\frac{1}{2}{.2}^{19}=2^{18}=262144$.

.

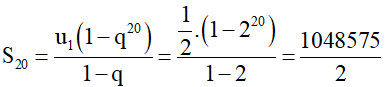
Vậy u₂₀ = 262144 và $S_{20}=\frac{1048575}{2}$.

B. Lý thuyết Cấp số nhân

1. Cấp số nhân

- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước nó với một số q không đổi, nghĩa là:

u_{n + 1} = u_n . q với n ∈ ℕ*.

Số q được gọi là công bội của cấp số nhân.

Ví dụ: Cho cấp số nhân (u_n) có u₁ = 3, u₂ = −6. Tìm công bội của cấp số nhân đã cho.

Hướng dẫn giải

Ta có: u₂ = u₁ . q ⇔ −6 = 3.q ⇔ q = −2.

Vậy công bội của cấp số nhân đã cho là −2.

2. Số hạng tổng quát của cấp số nhân

Định lí 1: Nếu một cấp số nhân (u_n) có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n của nó được xác định bởi công thức:

u_n = u₁ . q^{n – 1}, n ≥ 2.

Ví dụ: Cho cấp số nhân (u_n) có u₁ = 8 và q = −2. Tìm số hạng thứ năm của cấp số nhân đã cho.

Ta có: u₅ = u₁ . q^{5 – 1} = 8 . (−2)⁴ = 8 . 16 = 128.

Vậy số hạng thứ năm của cấp số nhân (u_n) là 128.

3. Tổng của n số hạng đầu tiên của cấp số nhân

Định lí 2: Giả sử (u_n) là một cấp số nhân có công bội q ≠ 1. Đặt S_n = u₁ + u₂ + ... + u_n, khi đó:

Chú ý: Khi q = 1 thì S_n = n . u₁.

Ví dụ: Cho cấp số nhân (u_n) có u₁ = 2, u₂ = −4. Tính S₄ của cấp số nhân đã cho.

Hướng dẫn giải

Ta có: u₂ = u₁ . q ⇔ −4 = 2.q ⇔ q = −2.

Video bài giảng Toán 11 Bài 7: Cấp số nhân - Kết nối tri thức