Tính quãng đường trung bình một cầu thủ chạy trong trận đấu này.

Lời giải: 

Quãng đường trung bình cầu thủ chạy trong trận đấu là:

$\frac{3,2 + 5,5 + 7,6 + 9,9 + 11,3}{2+5+6+9+3}=7,48\left(km\right)$

Bài 3.6 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tìm trung vị của mẫu số liệu này và giải thích ý nghĩa của giá trị thu được.

Lời giải:

Cỡ mẫu n = 2 + 5 + 6 + 9 + 3 = 25. Nhóm chứa trung vị là [6;80). Trung vị là:

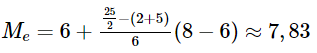
Có 50% số cầu thủ chạy nhiều hơn 7,83km và có 50% số cầu thủ chạy ít hơn 7,83km.

Bài 3.7 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tìm a sao cho có 25% số cầu thủ tham gia trận đấu chạy ít nhất a(km).

Lời giải:

Số a chính là tứ phân vị thứ ba.

Tứ phân vị thứ ba a là $\frac{x_{18}+x_{19}}{2}$. Do x₁₈; x₁₉ đều thuộc nhóm [8;10) nên nhóm này chứa a. Do đó, p = 4; a₄ = 8; m₄ = 9; m₁ + m₂ + m₃ = 2+5+6 = 13; a₅ - a₄ = 2

Suy ra: $a=8 +\frac{{\displaystyle \frac{3,25}{4}}-13}{9}.2=\frac{167}{18}$

Bài 3.8 trang 50 SBT Toán 11: Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tính mốt của mẫu số liệu và giải thích ý nghĩa của giá trị thu được

Lời giải:

Nhóm chứa mốt là [8; 10). Mốt là: 

Số cầu thủ chạy khoảng 8,67km là nhiều nhất.

Bài 3.9 trang 50 SBT Toán 11: Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:

Trung bình mỗi học sinh trong lớp đi muộn bao nhiêu buổi trong học kì?

Lời giải:

Ta có bảng số liệu ghép nhóm:

Trung bình mỗi học sinh trong học kì đi muộn số buổi là:

Bài 3.10 trang 50 SBT Toán 11: Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:

Tính các tứ phân vị của mẫu số liệu ghép nhóm và cho biết ý nghĩa của các kết quả thu được.

Lời giải:

Ta có bảng số liệu ghép nhóm:

Cỡ mẫu $n=40$

+ Tứ phân vị thứ nhất $Q_1$ là $\frac{x_{10}+x_{11}}{2}$. Do $x_{10},x_{11}$ đều thuộc nhóm $\left[0;3\right)$ nên nhóm này chứa $Q_1$. Do đó, $p=1,a_1=0,m_1=23,a_2-a_1=3$

Suy ra: $Q_1=0+\frac{\frac{40}{4}-0}{23}.3=\frac{30}{23}$

+ Tứ phân vị thứ ba $Q_3$ là $\frac{x_{30}+x_{31}}{2}$. Do $x_{30},x_{31}$ đều thuộc nhóm $\left[3;6\right)$ nên nhóm này chứa $Q_3$. Do đó, $p=2,a_2=3,m_2=8,m_1=233,a_3-a_2=3$

Suy ra: $Q_3=3+\frac{\frac{3.40}{4}-23}{8}.3=5,625$.

+ Tứ phân vị $Q_2$ chính là trung vị $M_e$

Nhóm chứa trung vị là $\left[0;3\right)$. Trung vị là: $M_e=0+\frac{\frac{40}{2}-0}{23}\left(3-0\right)=\frac{60}{23}$

Vậy $Q_2=\frac{60}{23}$.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 8: Mẫu số liệu ghép nhóm

Bài 9: Các số đặc trưng đo xu thế trung tâm

Bài tập cuối chương 3

Bài 10: Đường thẳng và mặt phẳng trong không gian

Bài 11: Hai đường thẳng song song

Lý thuyết Các số đặc trưng đo xu thế trung tâm

1. Số trung bình của mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là $\overline{x}=\frac{m_1{x}_1+...+m_k{x}_k}{n}$

Trong đó, $n=m_1+...+m_k$ là cỡ mẫu và $x_i=\frac{a_i+a_{i+1}}{2}$(với $i=1,2,...,k$) là giá trị đại diện của nhóm $[a_i;a_{i+1})$.

2. Trung vị của mẫu số liệu ghép nhóm

Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:

Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: $[a_p;a_{p+1})$.

Bước 2. Trung vị là $M_e=a_p+\frac{\frac{n}{2}-\left(m_1+...+m_{p-1}\right)}{m_p}.\left(a_{p+1}-a_p\right)$

Trong đó n là cỡ mẫu, $m_p$ là tần số nhóm p.

Với $p=1$, ta quy ước $m_1+...+m_{p-1}=0$

3. Tứ phân vị của mấu số liệu ghép nhóm

Để tính tứ phân vị thứ nhất $Q_1$ của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa $Q_1$, giả sử đó là nhóm thứ p: $[a_p;a_{p+1})$. Khi đó,

$Q_1=a_p+\frac{\frac{n}{4}-\left(m_1+...+m_{{}_{p-1}}\right)}{m_p}.\left(a_{p+1}-a_p\right)$

Trong đó n là cỡ mẫu, $m_p$ là tần số nhóm p.

Với $p=1$, ta quy ước $m_1+...+m_{p-1}=0$

Để tính tứ phân vị thứ ba $Q_3$ của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa $Q_3$, giả sử đó là nhóm thứ p: $[a_p;a_{p+1})$. Khi đó,

$Q_3=a_p+\frac{\frac{3n}{4}-\left(m_1+...+m_{{}_{p-1}}\right)}{m_p}.\left(a_{p+1}-a_p\right)$

Trong đó n là cỡ mẫu, $m_p$ là tần số nhóm p. Với $p=1$, ta quy ước $m_1+...+m_{p-1}=0$

Tứ phân vị thứ hai $Q_2$ chính là trung vị $M_e$.

4. Mốt của mẫu số liệu ghép nhóm

Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:

Bước 1. Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: $[a_j;a_{j+1})$.

Bước 2. Mốt được xác định là: $M_o=a_j+\frac{m_j-m_{j-1}}{\left(m_j-m_{j-1}\right)+\left(m_j-m_{j+1}\right)}.h$

Trong đó, $m_j$ là tần số của nhóm j (quy ước $m_0=m_{k+1}=0$) và h là độ dài của nhóm.

• Lưu ý:

Người ta chỉ định nghĩa mốt cho mẫu ghép nhóm có độ dài các nhóm bằng nhau. Một mẫu có thể không có mốt hoặc có nhiều hơn một mốt.

• Ý nghĩa:

Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc, nó được dùng để đo xu thế trung tâm của mẫu số liệu.