Với lời giải SBT Toán 11 trang 29 Tập 1 chi tiết trong Bài tập cuối chương 1 trang 25 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài tập cuối chương 1 trang 25

Bài 1.57 trang 29 SBT Toán 11 Tập 1: Hai sóng âm có phương trình lần lượt là

f1(t) = C sin ωt và f2(t) = C sin(ωt + α).

Hai sóng này giao thoa với nhau tạo ra một âm kết hợp có phương trình

f(t) =  f1(t) + f2(t) = C sin ωt + C sin(ωt + α).

a) Sử dụng công thức cộng chỉ ra rằng hàm f(t) có thể viết được dưới dạng f(t) = A sin ωt + B cos ωt, ở đó A, B là hai hằng số phụ thuộc vào α.

b) Khi C = 10 và $\alpha =\frac{\pi }{3}$, hãy tìm biên độ và pha ban đầu của sóng âm kết hợp, tức là tìm hai hằng số k và φ sao cho f(t) = k sin(ωt + φ).

Lời giải:

a) Ta có f(t) = f1(t) + f­­2(t)

= C sin ωt + C sin(ωt + α)

= C sin ωt + C(sin ωt cos α + cos ωt sin α)

= C sin ωt + C sin ωt cos α + C cos ωt sin α

= C(1 + cos α) sin ωt + C sin α cos ωt.

Vậy f(t) = C(1 + cos α) sin ωt + C sin α cos ωt với A = C(1 + cos α) và B = C sin α.

b) Khi C = 10 và $\alpha =\frac{\pi }{3}$ ta có

$f\left(t\right)=10\sin \omega t+10\sin \left(\omega t+\frac{\pi }{3}\right)$

$=10.2\sin \frac{\omega t+\omega t+\frac{\pi }{3}}{2}\cos \frac{\omega t-\omega t-\frac{\pi }{3}}{2}$

$=20\sin \left(\omega t+\frac{\pi }{6}\right)\cos \left(-\frac{\pi }{6}\right)$

$=10\sqrt{3}\sin \left(\omega t+\frac{\pi }{6}\right)$.

Vậy biên độ và pha ban đầu của sóng âm kết hợp lần lượt là $k=10\sqrt{3}$ và $\phi =\frac{\pi }{6}$.

Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:

a) $y=\cos \frac{2x}{x-1}$;

b) $y=\frac{1}{\cos x-\cos 3x}$;

c) $y=\frac{1}{\cos x+\sin 2x}$;

d) y = tan x + cot x.

Lời giải:

a) Biểu thức $\cos \frac{2x}{x-1}$ có nghĩa khi x – 1 ≠ 0 hay x ≠ 1.

Vậy tập xác định của hàm số là .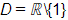

b) Biểu thức $\frac{1}{\cos x-\cos 3x}$ có nghĩa khi cos x – cos 3x ≠ 0 hay cos x ≠ cos 3x

⇔ 3x ≠ ± x + k2π (k ∈ ℤ) ⇔ x ≠ k$\frac{\pi }{2}$(k ∈ ℤ). .

Vậy tập xác định của hàm số là .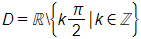

c) Biểu thức $\frac{1}{\cos x+\sin 2x}$ có nghĩa khi cos x + sin 2x ≠ 0 ⇔ cos x ≠ – sin 2x

⇔ cos x ≠ sin (– 2x) $\iff \cos x\ne \cos \left(\frac{\pi }{2}-\left(-2x\right)\right)$ $\iff \cos x\ne \cos \left(\frac{\pi }{2}+2x\right)$

Vậy tập xác định của hàm số là .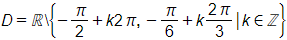

d) Biểu thức tan x + cot x có nghĩa khi

Vậy tập xác định của hàm số là .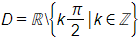

Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p

a) y = sin x – cos x;

b) y = sin x + sin$\left(\frac{\pi }{3}-x\right)$;

c) y = sin⁴ x + cos⁴ x;

d) y = cos 2x + 2cos x – 1.

Lời giải:

a) Ta có y = sin x – cos x = $\sqrt{2}\sin \left(x-\frac{\pi }{4}\right)$.

Vì $-1\le \sin \left(x-\frac{\pi }{4}\right)\le 1$ nên $-\sqrt{2}\le \sqrt{2}\sin \left(x-\frac{\pi }{4}\right)\le \sqrt{2}$, với mọi $x\in ℝ$.

Vậy giá trị lớn nhất của hàm số là $\sqrt{2}$, đạt được khi $\sin \left(x-\frac{\pi }{4}\right)=1$

$\iff x-\frac{\pi }{4}=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ $\iff x=\frac{3\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$>.

Giá trị nhỏ nhất của hàm số là $-\sqrt{2}$, đạt được khi $\sin \left(x-\frac{\pi }{4}\right)=-1$

$\iff x-\frac{\pi }{4}=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ $\iff x=-\frac{\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$.

b) Ta có y = sin x + sin$\left(\frac{\pi }{3}-x\right)$ $=2\sin \frac{x+\frac{\pi }{3}-x}{2}\cos \frac{x-\frac{\pi }{3}+x}{2}$

$=2\sin \frac{\pi }{6}\cos \left(x-\frac{\pi }{6}\right)$$=2.\frac{1}{2}\cos \left(x-\frac{\pi }{6}\right)=\cos \left(x-\frac{\pi }{6}\right)$.

Ta có $-1\le \cos \left(x-\frac{\pi }{6}\right)\le 1\forall x\in ℝ$.

Vậy giá trị lớn nhất của hàm số là 1, đạt được khi $\cos \left(x-\frac{\pi }{6}\right)=1$$\iff x-\frac{\pi }{6}=k2\pi \left(k\in \mathbb{Z}\right)$$\iff x=\frac{\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$ và giá trị nhỏ nhất của hàm số là – 1, đạt được khi $\cos \left(x-\frac{\pi }{6}\right)=-1$$\iff x-\frac{\pi }{6}=\pi +k2\pi \left(k\in \mathbb{Z}\right)$$\iff x=\frac{7\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$.

c) Ta có y = sin⁴ x + cos⁴ x = (sin² x + cos² x)² – 2sin² x cos² x

= 1 – 2 (sin x cos x)² = $1-2.{\left(\frac{\sin 2x}{2}\right)}^2$= $1-\frac{1}{2}{\sin }^{2}2x$ 

= $1-\frac{1}{2}.\frac{1-\cos 4x}{2}$ = $1-\frac{1}{4}+\frac{1}{4}\cos 4x$ = $\frac{3}{4}+\frac{1}{4}\cos 4x$.

Vì – 1 ≤ cos 4x ≤ 1 nên $-\frac{1}{4}\le \frac{1}{4}\cos 4x\le \frac{1}{4}$, do đó $\frac{3}{4}-\frac{1}{4}\le \frac{3}{4}+\frac{1}{4}\cos 4x\le \frac{3}{4}+\frac{1}{4}$

hay $\frac{1}{2}\le \frac{3}{4}+\frac{1}{4}\cos 4x\le 1\forall x\in ℝ$.

Vậy giá trị lớn nhất của hàm số là 1, đạt được khi cos 4x = 1 ⇔ 4x = k2π (k ∈ ℤ)

$\iff x=k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$.

Giá trị nhỏ nhất của hàm số là $\frac{1}{2}$, đạt được khi cos 4x = – 1 ⇔ 4x = π + k2π (k ∈ ℤ)

$\iff x=\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$.

d) Ta có y = cos 2x + 2cos x − 1

= (2cos² x – 1) + 2cos x – 1

= 2cos² x + 2cos x – 2

= 2t² + 2t – 2 với t = cos x ∈ [– 1; 1].

Xét hàm số y = 2t² + 2t – 2 trên đoạn [– 1; 1]. Hàm số này có đồ thị như trong hình vẽ dưới đây.

Từ đồ thị ở hình trên ta suy ra được giá trị lớn nhất của hàm số đã cho là 2, đạt được khi cos x = 1 ⇔ x = k2π (k ∈ ℤ) và giá trị nhỏ nhất của hàm số là $-\frac{5}{2}$, đạt được khi $\cos x=-\frac{1}{2}$$\iff x=\pm \frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right)$.

Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:

a) y = sin³ x – cot x;

b) $y=\frac{\cos x+{\tan }^{2}x}{\cos x}$;

c) y = sin 2x + cos x;

d) $y=2\cos \left(\frac{3\pi }{4}+x\right)\sin \left(\frac{\pi }{4}-x\right)$.

Lời giải:

a) Tập xác định của hàm số y = sin³ x – cot x là D = ℝ \ {kπ | k ∈ ℤ}.

Nếu kí hiệu f(x) = sin³ x + cot x thì với mọi x ∈ D ta có: – x ∈ D và

f(– x) = sin³ (–x) – cot(– x) = – sin³ x + cot x = –  (sin³ x – cot x) = – f(x).

Vậy hàm số đã cho là hàm số lẻ.

b) Tập xác định của hàm số $y=\frac{\cos x+{\tan }^{2}x}{\cos x}$ là 

Nếu kí hiệu $f\left(x\right)=\frac{\cos x+{\tan }^{2}x}{\cos x}$ thì với mọi x ∈ D ta có: – x ∈ D và

$$\begin{gathered} f\left(-x\right)=\frac{\cos \left(-x\right)+{\tan }^2\left(-x\right)}{\cos \left(-x\right)} \\ =\frac{\cos x+{\left(-\tan x\right)}^2}{\cos x}=\frac{\cos x+{\tan }^{2}x}{\cos x}=f\left(x\right) \end{gathered}$$

Vậy hàm số đã cho là hàm số chẵn.

c) Tập xác định của hàm số y = sin 2x + cos x là D = ℝ.

Nếu kí hiệu f(x) = sin 2x + cos x thì với mọi x ∈ D ta có: – x ∈ D và

f(– x) = sin [2(– x)] + cos (– x) = – sin 2x + cos x ≠ ± f(x).

Vậy hàm số đã cho là hàm số không chẵn cũng không lẻ.

d) Tập xác định của hàm số $y=2\cos \left(\frac{3\pi }{4}+x\right)\sin \left(\frac{\pi }{4}-x\right)$ là D = ℝ.

Ta có $y=2\cos \left(\frac{3\pi }{4}+x\right)\sin \left(\frac{\pi }{4}-x\right)$

$=\sin \pi +\sin \left(-\frac{\pi }{2}-2x\right)$$=0-\sin \left(\frac{\pi }{2}+2x\right)$

Nếu kí hiệu $f\left(x\right)=2\cos \left(\frac{3\pi }{4}+x\right)\sin \left(\frac{\pi }{4}-x\right)=-\cos 2x$ thì với mọi x ∈ D ta có: – x ∈ D và f(– x) = – cos (– 2x) = – cos 2x = f(x).

Vậy hàm số đã cho là hàm số chẵn.

Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau:

a) y = sin$\frac{x}{2}$ + cos 3x;

b) y = cos 5x + tan$\frac{x}{3}$.

Lời giải:

a) Hàm số y = sin$\frac{x}{2}$ tuần hoàn với chu kì T₁ = $\frac{2\pi }{\frac{1}{2}}=4\pi$, hàm số y = cos 3x tuần hoàn với chu kì T₂ = $\frac{2\pi }{3}$. Ta có $4\pi =6\cdot \frac{2\pi }{3}$.

Ta chỉ ra rằng hàm số f(x) = = sin$\frac{x}{2}$ + cos 3x tuần hoàn như sau:

$f\left(x+4\pi \right)=\sin \frac{x+4\pi }{2}+\cos 3\left(x+4\pi \right)$

          $=\sin \left(\frac{x}{2}+2\pi \right)+\cos \left(3x+12\pi \right)$

          $=\sin \frac{x}{2}+\cos 3x=f\left(x\right)\forall x\in ℝ$.

Vậy hàm số đã cho là hàm số tuần hoàn với chu kì T = 4π.

b) Hàm số y = cos 5x tuần hoàn với chu kì T₁ = null, hàm số y = tan$\frac{x}{3}$ hoàn với chu kì $T_2=\frac{\pi }{\frac{1}{3}}=3\pi$.

Ta có $6\pi =2\times 3\pi =15\times \frac{2\pi }{5}$.

Ta có thể chỉ ra hàm số f(x) = cos5x + tan$\frac{x}{3}$ tuần hoàn như sau

$f\left(x+6\pi \right)=\cos 5\left(x+6\pi \right)+\tan \frac{x+6\pi }{3}$

          $=\cos \left(5x+30\pi \right)+\tan \left(\frac{x}{3}+2\pi \right)$$=\cos 5x+\tan \frac{x}{3}=f\left(x\right)\forall x\in ℝ$.

Vậy hàm số đã cho là hàm số tuần hoàn với chu kì T = 6π.

Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau:

a) $\sin 3x=-\frac{\sqrt{3}}{2}$;

b) $\tan \left(\frac{x}{3}+10°\right)=-\frac{1}{\sqrt{3}}$;

c) sin 3x – cos 5x = 0;

d) tan 3x tan x = 1.

Lời giải:

a) Ta có $\sin 3x=-\frac{\sqrt{3}}{2}$

$\iff \sin 3x=\sin \left(-\frac{\pi }{3}\right)$

b) Ta có $\tan \left(\frac{x}{3}+10°\right)=-\frac{1}{\sqrt{3}}$

$\iff \tan \left(\frac{x}{3}+10°\right)=\tan \left(-30°\right)$

⇔ $\frac{x}{3}$ + 10° = – 30° + k180°  (k ∈ ℤ)

⇔ x = – 120° + k540° (k ∈ ℤ).

c) Ta có sin 3x – cos 5x = 0

⇔ sin 3x = cos 5x

$\iff \sin 3x=\sin \left(\frac{\pi }{2}-5x\right)$

d) Điều kiện cos 3x ≠ 0 và cos x ≠ 0 ⇔ cos3x ≠ 0 .

Ta có tan 3x tan x = 1

$\iff \tan 3x=\frac{1}{\tan x}$

⇔ tan 3x = cot x

$\iff \tan 3x=\tan \left(\frac{\pi }{2}-x\right)$

$\iff 3x=\frac{\pi }{2}-x+k\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\frac{\pi }{8}+k\frac{\pi }{4}\left(k\in \mathbb{Z}\right)$.

Ta thấy $x=\frac{\pi }{8}+k\frac{\pi }{4}\left(k\in \mathbb{Z}\right)$ thoả mãn điều kiện.

Vậy nghiệm của phương trình là $x=\frac{\pi }{8}+k\frac{\pi }{4}\left(k\in \mathbb{Z}\right)$.