Với giải Bài 1.51 trang 28 SBT Toán lớp 11 Kết nối tri thức chi tiết trong Bài tập cuối chương 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán lớp 11 Bài tập cuối chương 1
Bài 1.51 trang 28 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng.
a) ; b) ; c) – 1 380°.
Lời giải:
a) Ta có . Góc được biểu diễn bởi điểm trên đường tròn lượng giác (hình dưới).
Vậy và .
b) Ta có . Góс được biểu diễn bởi điểm > trên đường tròn lượng giác (hình dưới).
Vậy ; và .
c) Ta có – 1 380° = − 4 . 360° + 60°. Góc –1 380° được biểu diễn bởi điểm trên đường tròn lượng giác (hình dưới).
Vậy sin(– 1 380°) = ; cos(– 1 380°) = ; tan(– 1 380°) = và cot(– 1 380°) = .
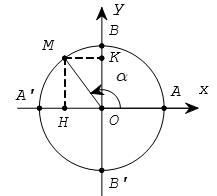
GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG α
1. Định nghĩa
Trên đường tròn lượng giác cho cung 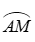
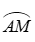
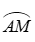
Tung độ y = 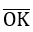
sin α =
Hoành độ x = 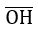
cos α =
Nếu cos α ≠ 0, tỉ số 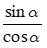
Tan α =
Nếu sinα ≠ 0 tỉ số 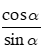
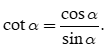
Xem thêm lời giải sách bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 1.31 trang 25 SBT Toán 11 Tập 1: Đổi số đo góc α = 105° sang rađian ta được....
Bài 1.33 trang 25 SBT Toán 11 Tập 1: Giá trị bằng...
Bài 1.34 trang 25 SBT Toán 11 Tập 1: Cho . Mệnh đề nào sau đây đúng?...
Bài 1.35 trang 25 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?...
Bài 1.36 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào đúng?....
Bài 1.37 trang 26 SBT Toán 11 Tập 1: Biết sin x = . Giá trị của cos2 x bằng...
Bài 1.38 trang 26 SBT Toán 11 Tập 1: Biết cot x = . Giá trị của biểu thức bằng....
Bài 1.39 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai....
Bài 1.40 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?..
Bài 1.41 trang 26 SBT Toán 11 Tập 1: Tập xác định của hàm số là...
Bài 1.42 trang 26 SBT Toán 11 Tập 1: Khẳng định nào sau đây đúng?...
Bài 1.43 trang 27 SBT Toán 11 Tập 1: Khẳng định nào sau đây sai?...
Bài 1.45 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?....
Bài 1.46 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?...
Bài 1.47 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào dưới đây đúng?.....
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau...
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x:....
Bài 1.57 trang 29 SBT Toán 11 Tập 1: Hai sóng âm có phương trình lần lượt là...
Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:...
Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p..
Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:....
Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau:...
Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau:...
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau:...
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: