Với lời giải Toán 8 trang 44 Tập 1 chi tiết trong Bài 9: Phân tích đa thức thành nhân tử sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải Toán 8 Bài 9: Phân tích đa thức thành nhân tử
Luyện tập 3 trang 44 Toán 8 Tập 1: Phân tích đa thức thành nhân tử.
Phương pháp giải:
Sử dụng cách nhóm hạng tử
Lời giải:
Vận dụng 2 trang 44 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức
tại
Phương pháp giải:
Phân tích đa thức thành nhân tử bằng cách nhóm hạng tử rồi thay các giá trị của x, y vào biểu thức.
Lời giải:
Thay vào A ta được:
Tranh luận trang 44 Toán 8 Tập 1: Phân tích đa thức thành nhân tử.
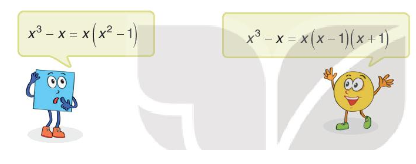
Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.
Phương pháp giải:
Kết hợp phương pháp đặt nhân tử chung và sử dụng hằng đẳng thức.
Lời giải:
Bạn Tròn có kết quả đúng, bạn Vuông chưa phân tích triệt để.
Bài tập
Bài 2.22 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
Phương pháp giải
Sử dụng phương pháp đặt nhân tử chung và sử dụng hằng đẳng thức.
Lời giải:
Bài 2.23 trang 44 Toán 8 Tập 1:
Phân tích các đa thức sau thành nhân tử:
a)
b)
Phương pháp giải
Phân tích đa thức thành nhân tử bằng cách nhóm hạng tử, sử dụng hằng đẳng thức.
Lời giải:
a)
b)
Bài 2.24 trang 44 Toán 8 Tập 1: Tìm x biết:
a)
b)
Phương pháp giải
Phân tích đa thức thành nhân tử.
Lời giải:
a)
Vậy
b)
Vậy
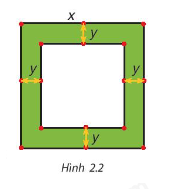
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính A khi x=102 m, y=2 m.
Phương pháp giải
Viết biểu thức.
Diện tích đường bao quanh = diện tích mảnh vườn hình vuông – diện tích bên trong vườn.
Phân tích đa thức thành nhân tử.
Lời giải:
a)
b)
Khi x=102 m, y=2 m thì ()
Video bài giảng Toán 8 Bài 9: Phân tích đa thức thành nhân tử - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Luyện tập 2 trang 43 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử....
Bài 2.22 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:...
Bài 2.23 trang 44 Toán 8 Tập 1: ....
Bài 2.24 trang 44 Toán 8 Tập 1: Tìm x biết:....
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 10: Tứ giác