Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài tập cuối chương 2 trang 47 chi tiết sách Toán 8 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài tập cuối chương 2 trang 47
A. Trắc nghiệm
Chọn phương án đúng trong những câu sau:
Bài 2.28 trang 47 Toán 8 Tập 1: Đa thức được phân tích thành tích của hai đa thức
A. và
B. và
C. và
D. và
Phương pháp giải
Tách hạng tử -9x thành 2 hạng tử bậc 1 có tích các hệ số là 8, tổng bằng -9 rồi phân tích đa thức thành nhân tử bằng cách nhóm hạng tử.
Lời giải:
Chọn B.
Bài 2.29 trang 47 Toán 8 Tập 1: Khẳng định nào sau đây là đúng?
A.
B.
C.
D.
Phương pháp giải
Sử dụng hằng đẳng thức
Lời giải:
Chọn D.
Bài 2.30 trang 47 Toán 8 Tập 1: Biểu thức viết dưới dạng bình phương của một tổng là:
A.
B.
C.
D. .
Phương pháp giải
Áp dụng hằng đẳng thức
Lời giải:
Chọn D.
Bài 2.31 trang 47 Toán 8 Tập 1: Rút gọn biểu thức ta được
A.
B.
C.
D.
Phương pháp giải
Áp dụng hằng đẳng thức và quy tắc nhân đơn thức với đa thức; cộng, trừ đa thức.
Lời giải:
Chọn C.
B. Tự luận
Bài 2.32 trang 47 Toán 8 Tập 1: Tính nhanh giá trị của các biểu thức:
a) tại x=102.
b) tại x=999.
Phương pháp giải
Sử dụng hằng đẳng thức để biến đổi biểu thức rồi thay các giá trị x vào biểu thức.
Lời giải:
a)
Thay vào biểu thức ta được
b)
Thay x=999 vào biểu thức ta được
Bài 2.33 trang 47 Toán 8 Tập 1: Rút gọn các biểu thức:
a)
b)
Phương pháp giải
a) Đặt nhân tử chung
b) Sử dụng hằng đẳng thức:
Lời giải:
a)
b)
Bài 2.34 trang 47 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a)
b)
c)
d)
Phương pháp giải
Sử dụng các hằng đẳng thức:
Lời giải:
a)
b)
c)
d)
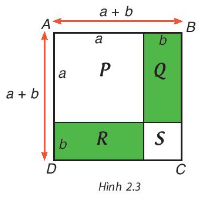
Phương pháp giải
Cách 1: Diện tích hình vuông bằng bình phương một cạnh.
Cách 2: Diện tích ABCD = Diện tích P + Q + R + S
Lời giải:
Diện tích hình vuông ABCD là:
Diện tích hình vuông ABCD là:
Do đó
Video bài giảng Toán 8 Bài tập cuối chương 2 trang 47 - Kết nối tri thức
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 10: Tứ giác
Bài 11: Hình thang cân
Luyện tập chung